
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Интегральное исчисление функций одного переменного
1. Интегральное исчисление функций одного переменного
1.1. Первообразная. Теоремы о первообразных. Неопределенный интеграл и его свойства. Таблица неопределенных интегралов.
Опр. Функция 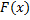 называется первообразной функции
называется первообразной функции  на
на 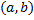 , если
, если 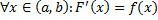 .
.
Пример. 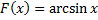 – первообразная функции
– первообразная функции 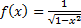 на интервале
на интервале 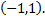
Теорема 1 (об арифметических свойствах первообразной).
Пусть 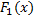 и
и 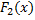 – первообразные функций
– первообразные функций  и
и 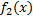 соответственно. Тогда функция
соответственно. Тогда функция 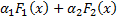 – первообразная функции
– первообразная функции 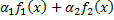 (
( 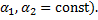
Док-во: 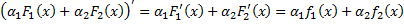 , т.е. функция
, т.е. функция 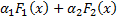 – первообразная функции
– первообразная функции 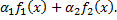

Теорема 2 (об общем виде первообразной).
Пусть 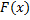 – первообразная функции
– первообразная функции  . Тогда любая первообразная функции
. Тогда любая первообразная функции  имеет вид
имеет вид
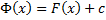 , где
, где 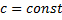
Док-во: т.к. 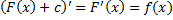 , то
, то 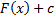 – тоже первообразная функции
– тоже первообразная функции  . Покажем, что любая первообразная имеет вид
. Покажем, что любая первообразная имеет вид 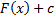 . Пусть
. Пусть  – первообразная функции
– первообразная функции  . Рассмотрим функцию
. Рассмотрим функцию 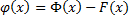 :
: 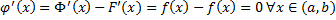 . Рассмотрим произвольные
. Рассмотрим произвольные 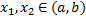 .
. 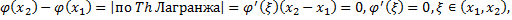 т.е.
т.е. 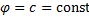 . Значит,
. Значит, 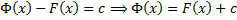
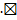
Опр. Совокупность всех первообразных функции  называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 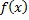 .
.
Обозн.: 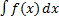 .
.
Пусть 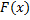 – первообразная функции
– первообразная функции  . Тогда
. Тогда 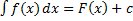 , где
, где 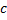 – произвольная постоянная.
– произвольная постоянная.
Пример. 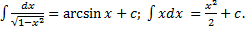
Свойства неопределенного интеграла:
1. 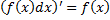
2. 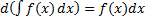
3. 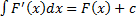 или
или 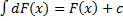
4. 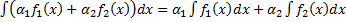 , где
, где 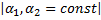
Док-во:
1. 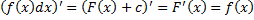 , где
, где 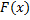 – первообразная функции
– первообразная функции 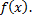
2. 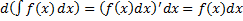 .
.
3. Т.к. 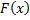 – первообразная
– первообразная 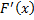 , то
, то 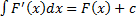 .
.
4. Пусть 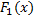 и
и 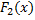 – первообразные функций
– первообразные функций  и
и 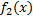 соответственно.
соответственно.
Тогда функция 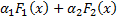 – первообразная функции
– первообразная функции 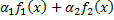 (
( 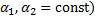 . Отсюда
. Отсюда 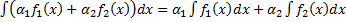

Таблица интегралов:
1. 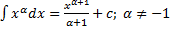
2.  . (Т.к. при
. (Т.к. при 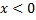
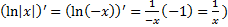
3. 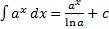 (
( 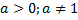 )
)
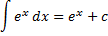
4. 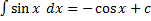
5. 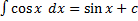
6. 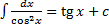
7. 
8. 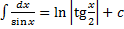
9. 
10. 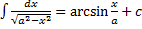 ,
, 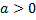
11. 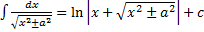 ,
, 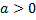 (длинный логарифм)
(длинный логарифм)
12. 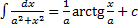 ,
,
13. 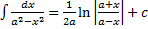 или
или 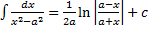 (высокий логарифм)
(высокий логарифм)
14. 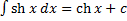
15. 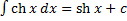
16. 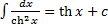
17. 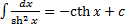
Примеры.
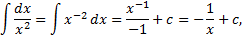

1.2. Интегрирование подстановкой и по частям. Примеры. Интегрирование выражений, содержащих квадратный трехчлен. Интегрирование тригонометрических и иррациональных функций.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|