А.В. Неклюдов. Интегралы и . диффереренциальные уравнения. Электронное учебное издание

Стр 1 из 28Следующая ⇒

Московский государственный технический университет

имени Н.Э. Баумана

Факультет фундаментальные науки»

Кафедра «Высшая математика»

А.В. Неклюдов

Интегралы и

диффереренциальные уравнения

Электронное учебное издание

Лекции по курсу

Москва

(С)2013 МГТУ им. Н.Э. Баумана

УДК: 517.3

Рецензент:

Неклюдов А.В., Интегралы и дифференциальные уравнения. Лекции по курсу" - М., МГТУ им. Н.Э. Баумана, илл. 42.

Изложены основы интегрального исчисления функций одной переменной и теории обыкновенных дифференциальных уравнений. Большая часть теории излагается с подробными доказательствами, пояснениями и примерами.

Для студентов, изучающих и применяющих математический анализ и обыкновенные дифференциальные уравнения.

Рекомендовано Учебно-методической комиссией факультета "Фундаментальные науки" МГТУ им. Н.Э. Баумана.

Оглавление

1. Интегральное исчисление функций одного переменного. 5

1.1. Первообразная. Теоремы о первообразных. Неопределенный интеграл и его свойства. Таблица неопределенных интегралов. 5

1.2. Интегрирование подстановкой и по частям. Примеры. Интегрирование выражений, содержащих квадратный трехчлен. Интегрирование тригонометрических и иррациональных функций. 6

1.3. Интегрирование рациональных дробей. Разложение правильной рациональной дроби в сумму простейших. Интегрирование простейших дробей. Интегрирование неправильных рациональных дробей. 11

1.4. Определенный интеграл, его механический и геометрический смысл, теорема существования. Линейность и аддитивность определенного интеграла. 14

1.5. Определенный интеграл с переменным верхним пределом. Теорема о производной интеграла с переменным верхним пределом. Формула Ньютона-Лейбница. 17

1.6. Вычисление определенного интеграла подстановкой и по частям. Интегрирование четных и нечетных функций на отрезке, симметричном относительно начала координат, интегрирование периодических функций. 18

1.7. Несобственные интегралы 1-го и 2-го рода, их свойства. Признаки сходимости. Абсолютная и условная сходимость несобственных интегралов. 20

1.8. Вычисление площадей плоских фигур в декартовых и полярных координатах. 26

1.9. Вычисление объемов тел по площадям поперечных сечений и объемов тел вращения. 29

1.10. Вычисление длин дуг кривых и площадей поверхностей вращения. 31

2. Обыкновенные дифференциальные уравнения. 33

2.1.Задачи, приводящие к дифференциальным уравнениям (ДУ). ДУ 1-го порядка. Частные и общее решения ДУ, интегральные кривые. Задача Коши и теорема существования и единственности ее решения. Особые точки и особые решения ДУ. 34

2.2. Геометрическая интерпретация ДУ 1-го порядка. Поле направлений. Геометрическое решение ДУ 1-го порядка с помощью изоклин. 36

2.3. Простейшие типы ДУ 1-го порядка (с разделяющимися переменными, однородные, линейные, Бернулли) и их решение. 38

2.4. ДУ n-го порядка. Частные и общее решения. Задача Коши, ее геометрическая интерпретация при n=2. Теорема существования и единственности решения задачи Коши. Краевая задача. 42

2.5. Понижение порядка некоторых типов ДУ высших порядков. 43

2.6. Линейные ДУ (ЛДУ) n-го порядка: однородные (ЛОДУ) и неоднородные (ЛНДУ). Теорема существования и единственности решения. Линейный дифференциальный оператор. Свойства линейного дифференциального оператора и линейность пространства решений ЛОДУ. 44

2.7. Линейная зависимость функций. Определитель Вронского (вронскиан). Теорема о вронскиане системы линейно зависимых функций и о вронскиане системы линейно независимых частных решений ЛОДУ. 45

2.8. Теорема о размерности пространства решений ЛОДУ n-го порядка. Фундаментальная система решений. Структура общего решения. 48

2.9. Формула Остроградского-Лиувилля для ЛОДУ n-го порядка и ее следствия. 49

2.10. Теорема о структуре общего решения неоднородного ЛДУ n-го порядка. Теорема о наложении частных решений. 51

2.11. ЛОДУ с постоянным коэффициентами. Характеристическое уравнение и построение общего решения по его корням (вывод для 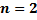). 51

2.12. Нахождение частных решений неоднородного ЛДУ с постоянными коэффициентами и правой частью специального вида. 54

2.13. Метод вариации постоянных решения неоднородных ЛДУ n-го порядка (вывод для 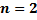). 57

2.14. Нормальные системы ДУ. Задача Коши и теорема существования и единственности ее решения. Сведение ДУ n-го порядка к нормальной системе. Сведение нормальной системы к одному уравнению n-го порядка. 59

2.15. Автономные системы ДУ. Фазовое пространство и фазовые траектории. Первые интегралы систем ДУ. Симметричная форма записи систем ДУ и ее применение к нахождению первых интегралов. 61

2.16. Нормальные системы ЛДУ, однородные и неоднородные. Матричная запись системы. Линейность пространства решений системы ЛОДУ. Вронскиан системы вектор-функций и его свойства. Теорема о размерности пространства решений системы ЛОДУ. Структура общего решения. Фундаментальная система решений. 66

2.17. Системы ЛОДУ с постоянными коэффициентами. Характеристическое уравнение. Построение общего решения по корням характеристического уравнения (вывод для случая вещественных различных корней) 68

12 3 4 5 6 7 8 9 10 Следующая ⇒