(Чекин М2класс 2часть стр81). (Чекин М2класс 2часть стр.82). (Чекин М2класс 2часть стр.83)

(Чекин М2класс 2часть стр81)

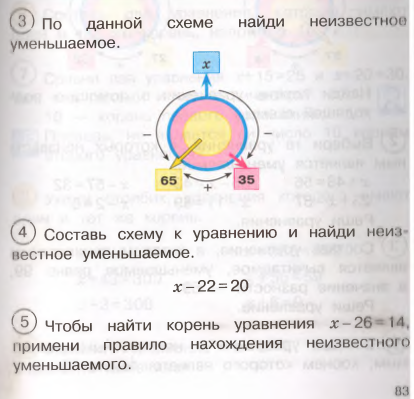
При изучении темы учащиеся познакомятся с правилом, которое позволяет решать уравнения с неизвестным уменьшаемым. Вывод соответствующего правила будет проведен совершенно аналогично тому, как это было сделано для правил нахождения неизвестного слагаемого и неизвестного вычитаемого. При выполнении задания1 учащиеся должны самостоятельно разобраться в вопросе построения круговой схемы для уравнения с неизвестным уменьшаемым. Для того чтобы акцентировать внимание учащихся на ключевых моментах заполнения круговой схемы, мы предлагаем систему вопросов, на которые учащиеся должны ответить самостоятельно

(Чекин М2класс 2часть стр. 82)

В задании2 продолжается работа по выводу интересующего нас правила. На данном этапе рассуждений учащиеся должны выбрать действие для нахождения неизвестного уменьшаемого, после чего провести вычисления и сделать обобщение в виде соответствующего правила.

(Чекин М 2 класс 2часть стр 82 – 83)

Выполняя задания 3, 4, 5 дети закрепляют изученный материал

(Чекин М2класс 2часть стр. 83)

Учимся решать уравнения

В теме дается подборка заданий, с помощью которых подводится некоторый итог по изучению вопросов, связанных с уравнениями и способами их решения. Этой работе можно целенаправленно посвятить один или два урока, но можно рассредоточить данный материал и использовать его для закрепления и повторения, а также в качестве домашних заданий. На данном этапе изучения уравнений и способов их решения мы предлагаем, по возможности, не употреблять термин «решение уравнения», а говорить о нахождении корня уравнения. Связано это с тем, что под решением уравнения понимают, как правило, множество всех корней данного уравнения, в том числе не исключается и случай, когда уравнение не имеет ни одного корня.

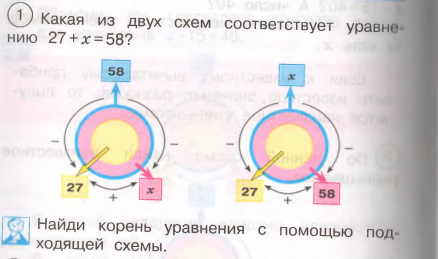
В задании 1 сначала предлагается распознать готовую круговую схему, которая соответствует данному уравнению с неизвестным слагаемым. Такая форма работы направлена на формирование умения составлять круговую схему по данному уравнению. После того как нужная схема будет выбрана, остается применить ее для нахождения корня уравнения

( Чекин М2класс 2часть стр. 84)

Задания2, 3 и4 направлены на закрепление полученных знаний о трех типах простейших уравнений и правил, позволяющих решать эти уравнения.

(Чекин М2класс 2часть стр. 84)

Запись решения задачи ввиде уравнения

При изучении данной темы мы не только возвратим учащихся крассмотрению вопросов алгебраического характера, но и продемонстрируем возможность применения алгебраических понятий при решении арифметических задач. Итак, в данной теме речь пойдет об уравнении как об одном возможном способе записи решения задачи. Более детально о правомерности такой постановки вопроса было сказано выше вобщих рекомендациях по изучению алгебраического материала. Алгоритмический характер решения задачи спомощью уравнения вданном случае может быть истолкован следующим образом:

- найди корень соответствующего уравнения;

- проверь;

-подходит ли он по смыслу задачи;

-этот корень и будет являться ответом на требование задачи

В задании1 учащимся объясняется, как можно составить уравнение, которое будет являться решением данной задачи. Обоснование того, что соответствующее уравнение можно считать решением данной задачи, для учащихся должно состоять вследующем.

(Чекин М 2класс 2часть стр. 146 – 147)

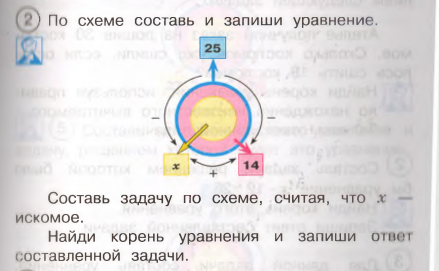
В задании2 предлагается решить задачу с помощью составления уравнения, но сама процедура будет представлена внесколько ином виде. Им предлагается сразу рассмотреть готовую схему для составления уравнения. Отталкиваясь от этой схемы, учащиеся должны осуществить логическое продвижение вдвух направлениях. Во-первых, они должны по этой схеме составить уравнение. Во-вторых, по этой же схеме они должны составить задачу. Если обе части задания выполнены правильно, то можно утверждать, что корень составленного уравнения будет являться ответом составленной задачи.

( Чекин М2класс 2часть стр147)

⇐ Предыдущая 1 2 3 4 567 8 9 Следующая ⇒