до лабораторної роботи №1. з курсу «Системи підтримки прийняття рішень». «Підтримка прийняття рішень при оцінюванні альтернатив за одиничним критерієм». Князик Ю.М.. Верес О.М.

Міністерство освіти і науки, молоді та спорту України

Національний університет «Львівська політехніка»

Кафедра Інформаційні системи та мережі

ЗВІТ

до лабораторної роботи №1

з курсу «Системи підтримки прийняття рішень»

на тему:

«Підтримка прийняття рішень при оцінюванні альтернатив за одиничним критерієм»

Виконав:

студент групи CA-41

Князик Ю. М.

Прийняв:

доцент

Верес О. М.

Львів-2013

Мета роботи:

Завдання:

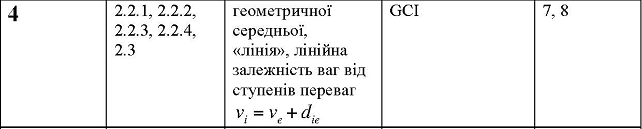
Хід роботи:

За даними задачі будуємо МПП у фундаментальній шкалі:

За умовами мультиплікативної нормалізації шукаємо ваги:

V₁= (3)^1/4= 1, 316

V₂ = (15)^1/4 = 1, 968

V₃ = (1/75)^1/4 = 0, 34

V₄ = (5/3)^1/4= 1, 136

Тоді нормовані до одиниці ваги альтернатив розраховуються за формулою:

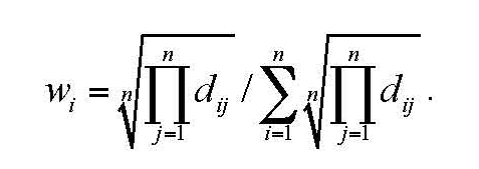
Suma = 1, 316 + 1, 968 + 0, 34 + 1, 136 = 4, 76.

Тоді:

W₁= 1, 316 / 4, 76 = 0, 276

W₂ = 1, 968 / 4, 76 = 0, 413

W₃ = 0, 34 / 4, 76 = 0, 071

W₄ = 1, 136 / 4, 76 = 0, 239

Геометричний індекс узгодженості (GCI) обчислюється за формулою:

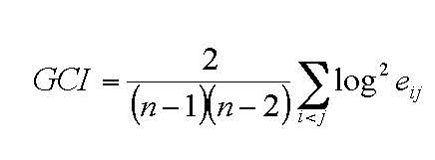
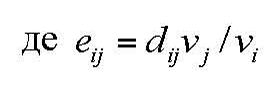
e₁₂ = 1, 495

e₁₃ = 0, 775

e₁₄= 0, 863

e₂₃= 0, 864

e₂₄= 1, 731

e₃₄= 0, 668

SUMA = 0, 03 + 0, 012 + 0, 004 + 0, 004 + 0, 057 + 0, 031 = 0, 169

Тепер рахуємо GCI:

GCI = (2*0, 169) / 6 = 0, 0562

Порівнюємо з табличним GCI = 0, 3526. Бачимо, що отримане GCI менше за табличне, отже оцінки експертів є узгодженими.

Висновок: я оцінив коефіцієнти ваг за методом геометричної середньої та оцінив узгодженість експертних оцінок за показником GCI.