Хелпикс

Главная

Контакты

Случайная статья



Неопределенный интеграл и его свойства.

Стр 1 из 24Следующая ⇒


Неопределенный интеграл и его свойства.

Определение 1.: Функция F(x) называется первообразной для функции ƒ(x) на некотором отрезке [a,b], если для всех из этого отрезка выполняется равенство:

F'(x)= ƒ(x).

Теорема1. Если F1(x) и F2(x) какие-либо первообразные для функции ƒ(x) на отрезке [a,b], то выполняется соотношение:

F1(x) — F2(x) = C;

Определение 2.:Совокупность первообразных, т.е. (F(x)+С), для ƒ(x) на [a,b] называется неопределенным интегралом от f(x) и обозначается:

∫ƒ(x) dx = F(x) + C, причем F'(x) = ƒ(x),

ƒ(x) — называется подынтегральной функцией;

ƒ(x)dx — называется подынтегральным выражением;

Свойства неопределенного интеграла:

1.(∫ƒ(x)dx)' = ƒ(x);

2. d ∫ƒ(x)dx = ƒ(x)dx;

3. ∫d F(x) = F(x) + C;

4. ∫(ƒ1(x)+ ƒ2(x))dx =∫ƒ1(x)dx + ∫ƒ2(x)dx.

5. ∫k·ƒ(x)dx = k·∫ƒ(x)dx, где k — постоянный множитель.

6. Формулы интегрирования не меняет свой вид при подстановке вместо независимой переменной x некоторой функции u(x), т.е. если∫ƒ(x)dx = F(x) + C;

∫ƒ(u)du = F(u) + C;

 

Таблица интегралов

Площадь плоской фигуры                                Длина дуги                         Объем тела вращения

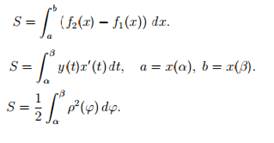
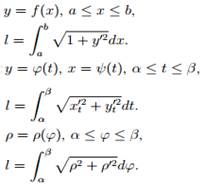
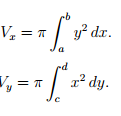
Определенный интеграл и его свойства

I.. 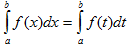, где х, t – любые буквы.

II.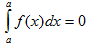

III.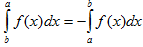

IV.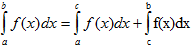

V.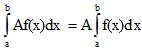

VI.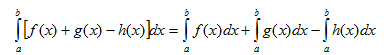

7.

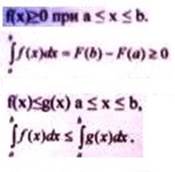
Свойства двойного интеграла


12345678910Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.