Техника расчета 8 страница

r_S = 0,855

КОРРЕЛЯЦИЯ МЕЖДУ КАЧЕСТВЕННЫМИ ПРИЗНАКАМИ

В случае альтернативного разнообразия, когда исследуются качественные признаки, выражающиеся наличием или отсутствием их у животного, корреляционная связь между признаками измеряется тет-рахорическим показателем связи, предложенным в 1901 г. К. Пирсоном:

r_A = ,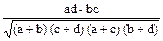

где а - число особей, имеющих оба исследуемых признака;

b - число особей, имеющих первый признак, но не имеющих второго;

с - число особей, не имеющих первого признака, но имеющих второй;

d - число особей, не имеющих оба признака.

ПРЯМОЛИНЕЙНАЯ РЕГРЕССИЯ, ЕЕ КОЭФФИЦИЕНТ И УРАВНЕНИЕ

При линейном типе связи между двумя изучаемыми признаками кроме расчета корреляций применяется расчет коэффициента регрессии.

В случае прямолинейной корреляционной связи каждому из изменений одного признака соответствует вполне определенное изменение другого признака. Однако коэффициент корреляции показывает эту связь лишь в относительных величинах - в долях единицы. С помощью же регрессионного анализа эту величину связи получают в именованных единицах. Та величина, на которую в среднем изменяется первый признак при изменении второго на единицу измерения, называется коэффициентом регрессии.

В отличие от корреляционного, регрессионный анализ дает более широкую информацию, поскольку вычислением двух коэффициентов регрессии R_x_/_y и R_у/х возможно определить как зависимость первого признака от второго, так и второго от первого. Выражение регрессионной связи с помощью уравнения позволяет по определенному значению одного признака установить значение другого признака.

Коэффициент регрессии R представляет собой произведение коэффициента корреляции на отношение квадратических отклонений, вычисленных для каждого признака. Рассчитывается он по формуле

R_x_/_y = r ´ ,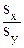

где R - коэффициент регрессии; S_Х - среднее квадратическое отклонение первого признака, который изменяется в связи с изменением второго; S_У - среднее квадратическое отклонение второго признака, в связи с изменением которого изменяется первый признак; r - коэффициент корреляции между этими признаками; х - функция; у -аргумент.

По этой формуле определяется величина значения х при изменении у на единицу измерения. При необходимости обратного расчета можно найти величину у при изменении х на единицу измерения по формуле:

R_у/х = r ´ .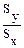

В этом случае активная роль в изменении одного признака по отношению к другому меняется, по сравнению с предыдущей формулой аргумент становится функцией, и наоборот. Величины S_X и S_Y принимаются в именованном выражении.

Между значениями г и R имеется четкая взаимосвязь, выражающаяся в том, что произведение регрессии х по у на регрессию у по х равно квадрату коэффициента корреляции, т. е.

R_x_/_y ´ R_y_/_x = r² .

Это свидетельствует, что коэффициент корреляции представляет собой среднюю геометрическую из обоих значений коэффициентов регрессии данной выборки. Данная формула может быть использована для проверки правильности расчетов.

При обработке цифрового материала на счетных машинах могут применяться развернутые формулы коэффициента регрессии:

или

R_x_/_y =

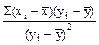
R_x_/_y = .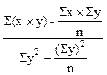

Для коэффициента регрессии может быть рассчитана его ошибка репрезентативности. Ошибка коэффициента регрессии равна ошибке коэффициента корреляции, умноженной на отношение квадратических отношений:

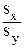S_R = ´S_r = ´ .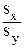

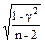Критерий достоверности коэффициента регрессии вычисляется по обычной формуле:

t_R = .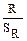

В итоге он равен критерию достоверности коэффициента корреляции:

t_R = 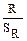= = 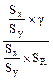= 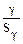t_r .

Достоверность величины t_R устанавливается по таблице Стьюдента при n = n - 2, где n - число пар наблюдений.

Предположим, что при расчете коэффициента корреляции между уровнем яйценоскости и массой яиц:

было установлено, что r = -0,46;

для показателя яйценоскости: 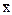= 102; S = 7,0; n = 40

для показателя массы яйца: 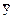= 56,68; S = 1,94;n = 40

регрессия первого признака по второму равна:

R_x_/_y = 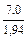´(-0,46) = 3,61´(-0,46) = -1,66 .

Это означает, что увеличение массы яйца на 1 г в данной популяции кур сопровождается уменьшением яйценоскости за 5 мес. на 1,66 яйца.

Обратный расчет:

R_y_/_x = 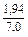´(-0,46) = 0,277´(-0,46) = -0,127

показывает, что повышение яйценоскости на 1 яйцо за 5-месячный период в данной популяции кур сопровождается уменьшением средней массы яиц на 0,127 г.

По формуле взаимозависимости r и R можно проверить правильность расчета:

(-1,66) ´ (-0,127) = 0,210; (-0,46)² = 0,210.

Ошибка коэффициента регрессии R_x_/_y = равна

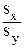S_R = ´S_r = ´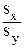

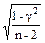
S_R = 3,61´ 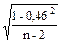= 3,61´ 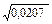= 3,61´0,144 = 0,52

S_R = 0,52 .

Критерий достоверности R_x_/_y равен

t_R = 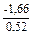= 3,19 .

По таблице Стьюдента стандартные значения t для n = 38 равны 2,0-2,7-3,6. Следовательно, рассчитанный коэффициент регрессии достоверен при Р ³ 0,99.

Более глубокий анализ связи двух признаков может быть сделан на основе расчета уравнения прямолинейной регрессии. Сущность коэффициента прямолинейной регрессии, показывающей, насколько второй признак отклоняется от своей средней, если первый отклоняется от своей средней на единицу измерения, можно выразить формулой

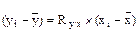Преобразуя это уравнение, получаем рабочую формулу прямолинейной регрессии. Обозначаем R_y/x через b:

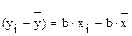
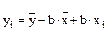Обозначаем 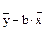= а, следовательно

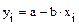В этом уравнении х является аргументом, у - его функцией. Уравнение показывает взаимоотношение между аргументом и функцией, именно то взаимоотношение признаков, которое и образует коэффициент регрессии. По этой формуле, зная значения аргумента (х), можно определить значение его функции (у) без непосредственного ее измерения.

В рассмотренном выше примере были вычислены коэффициенты корреляции и регрессии между уровнем яйценоскости и массой яиц у кур. Если принять яйценоскость кур за аргумент, можно составить следующее уравнение прямолинейной регрессии:

;

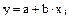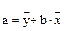
а = 56,68 - (-0,127) ´ 102 = 56,68 + 12,95 – 69,63; а = 69,63

у = 69,63 + (-0,127) ´ x = 69,63 – 0,127 ´ x .

Таким образом, чтобы установить, какая масса яйца может соответствовать тому или иному уровню яйценоскости, нужно умножить показатель яйценоскости на коэффициент 0,127 и вычесть это произведение из числа 69,63. На основе этого уравнения можно заранее рассчитать значение функций для каждого значения аргумента. В частности, в данном примере можно составить ряд, показывающий регрессионные зависимости яйценоскости и массы яиц в данной популяции кур.

Таблица 30

Теоретический ряд регрессии между признаками яйценоскости кур

за 5 мес. и массой яиц

Яйценоскость
Масса яиц	58,8	58,2	57,6	56,9	56,3	55,7	55,0	54,4

Эта таблица может быть полезна в селекционной работе, так как она дает основание предъявлять требования к массе яиц не вообще, а в связи с уровнем яйценоскости, т.е. на основании биологической взаимосвязи этих двух показателей. В частности, масса яйца в 57 г может быть оценена как весьма небольшая для курицы, снесшей за 5 мес. 90 яиц, но она будет очень хорошей для курицы, снесшей за тот же период 120 яиц.

Для успешной работы с той или иной популяцией животных зоотехник-селекционер может построить аналогичные таблицы по основным селекционируемым признакам.

ДИСПЕРСИОННЫЙ АНАЛИЗ

Сущность метода, основные показатели

Дисперсионный, или вариансный, анализ разработан английским математиком и биологом Р. Э. Фишером (1890-1962) и опубликован в 1925 г. В настоящее время этот метод очень широко применяется в статистической обработке цифровых материалов, получаемых в экспериментах с биологическими объектами - животными, растениями, бактериями. Он является основой расчетов данных экспериментов, построенных по схеме факториального опыта.

Сущность дисперсионного анализа состоит в изучении статистического влияния одного или нескольких факторов на изучаемый результативный признак и определении достоверности этого влияния. Основным содержанием дисперсионного анализа является разложение общей изменчивости признака (или его разнообразия) на частную изменчивость, возникающую под влиянием различных факторов.

Выше обсуждался вопрос о варьировании признаков у биологических объектов. Это варьирование признаков обусловлено действием многочисленных факторов. Часть этих факторов, влияя на признак, изменяет его в сторону увеличения, другие факторы, наоборот, могут обусловливать его уменьшение. Одни факторы оказывают большее влияние на признак, другие - меньшее. Факторы могут оказывать совместное влияние на изменчивость признака, объединяя свое действие, что создает дополнительный источник изменчивости. Факторы, влияющие на признак, могут существенно различаться по своей природе, прежде всего это могут быть факторы внешнего порядка (различные факторы внешней среды) и факторы внутреннего порядка (факторы, обусловленные природой организма, генетические).

В результате суммарного действия всех воздействующих на организм факторов во всем их многообразии возникает биологическое варьирование признаков. Эту конечную общую изменчивость специалист наблюдает в практической работе при изучении любой совокупности объектов. Чтобы изучить закономерности изменчивости объектов в той или иной совокупности, важно выделить долю влияния отдельных факторов, прежде всего тех, которые представляют интерес в конкретном исследовании. В специальном эксперименте такие факторы учитываются особо, они называются учтенными или организованными. Обрабатывая цифровой экспериментальный материал дисперсионным методом, можно определить математическое выражение и величину изменчивости, обусловленную действием учтенных в опыте факторов, и изменчивость, обусловленную всеми другими факторами, которые в опыте не были учтены, т. е. остаточную и случайную. Именно в этом расчленении общей изменчивости признаков состоит первое и наиболее важное назначение дисперсионного анализа.

Вторым важным назначением дисперсионного анализа является то, что он позволяет определить статистическую достоверность влияния каждого изучаемого фактора. Для того чтобы определить степень и достоверность влияния изучаемых факторов, необходимо, прежде всего, измерить ту часть общего разнообразия, которая вызывается этими факторами. Это достигается расчетом дисперсии и вариансы.

Дисперсия является основным элементом этого анализа и ее получение составляет его основную задачу. Дисперсией в математическом выражении обозначается как само разнообразие, так и первичная мера, определяющая степень этого разнообразия. В предыдущих разделах определено, что дисперсия как первичная мера разнообразия представляет собой сумму квадратов центральных отклонений:

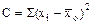В данном случае центральные отклонения представляют собой отклонения каждой даты, входящей в статистический комплекс, от средней арифметической величины по всему комплексу. Представление об этих общих отклонениях можно получить из следующей схемы:

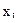
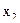
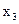
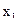
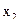
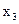
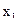
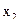
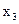
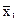
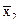
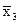
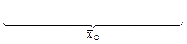
Через С_Y обозначается общая дисперсия, характеризующая в целом по комплексу разнообразие признака, обусловленное всеми влияющими на него факторами.

Общее разнообразие результативного признака всегда больше того разнообразия, которое связано со статистическим влиянием организованных факторов. Дело в том, что ни в одном исследовании, даже идеально организованном, нельзя освободиться от множества остальных факторов, так или иначе влияющих на изменение результативного признака (как правило, это и не требуется).

При дисперсионном анализе общая дисперсия признака С_Y расчленяется на дисперсию, обусловленную организованными факторами, или факториальную (частную) дисперсию С_Х , а также на дисперсию, обусловленную остальными, неорганизованными в данном опыте факторами, или случайную (остаточную) дисперсию С_Z .

Общая дисперсия всегда равна сумме факториальной и случайной дисперсий С_Y = С_Х + С_Z.

Если общая дисперсия, показывающая общее разнообразие признака в изучаемой совокупности, представляет собой сумму квадратов разностей между величиной признака и общей для совокупности средней арифметической :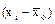

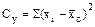то факториальная дисперсия (С_Х) характеризует межгрупповое разнообразие и рассчитывается как сумма квадратов разностей между величиной частной средней арифметической ( 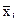)и общей средней арифметической ( ):

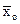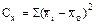Случайная дисперсия, в свою очередь, характеризует внутригруп-повое разнообразие и представляет сумму квадратов разностей между величиной варьирующего признака (Х_i) и частной средней арифметической ( ):

Сумма отношений частных дисперсий к общей всегда равна единице. Каждое такое отношение показывает долю участия отдельного фактора в формировании общего разнообразия результативного признака. В этой связи такие отношения рассматриваются как показатели степени влияния тех или иных факторов на результативный признак:

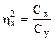и .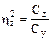

Как показатель разнообразия, дисперсия зависит от числа особей в группе (от объема выборки). В частности, при расчете степени влияния это не имеет значения, но для получения других важных показателей необходимо освободить величину, определяющую разнообразие признака, от этой зависимости, с тем чтобы сравнивать группы, различные по числу входящих в них элементов. Для этого рассчитывается девиата, или варианса.

Вариансой называется величина дисперсии, приходящаяся на один элемент свободного разнообразия или на одну степень свободы, таким образом варианса равна сумме квадратов центральных отклонений, деленной на число степеней свободы:

S² = ,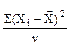

где n - число степеней свободы.

В зависимости от исходной величины дисперсии может раcсчитываться варианса общая по всему комплексу S²_y , частная варианса по организованным факторам S²_x или частная варианса по случайным (неорганизованным) факторам S²_z.

В дисперсионном анализе вариансы используются для определения достоверности влияния, обнаруженного в выборочном исследовании. Достоверность влияния фактора определяется отношением факториаль-ной вариансы к случайной:

F = .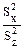

Полученная величина F называется критерием Фишера. Величина F-эмпирическая сравнивается с величиной F-теоретической, или стандартной. Стандартные значение F приведены в специальных таблицах (приложение 1). В этих таблицах на пересечениях строчек и столбцов, означающих числа степеней свободы υ₁ и υ₂, проставлены теоретические величины F для трех уровней вероятности (Р = 0,95; Р = 0,99; Р = 0,999). Как правило, число степеней свободы υ₂ соответствует n_z, а n₁ соответствует n_x. Если F эмпирический >F теоретический, то это позволяет говорить о достоверном влиянии изучаемого фактора на результативный признак.

Определение достоверности влияния фактора с помощью критерия Фишера основывается на понятии нулевой гипотезы, которая содержит в себе утверждение, что изучаемые дисперсионным анализом факторы не оказывают достоверного влияния на результативный признак. Если величина F, вычисленная для конкретного комплекса, равна 1, то нулевая гипотеза сохраняется, т. е. воздействие факторов на результативный признак отсутствует. Если F эмп. < F теор., то нулевая гипотеза также остается в силе, поскольку имеющаяся вариабельность результативного признака обусловлена случайными факторами.

Если же вычисленное значение F окажется больше табличного значения F, значит, оно выходит за пределы случайных отклонений. Следовательно, нулевая гипотеза отвергается и признается достоверное влияние фактора на результативный признак. Критерий F в случае F эмп.>F теор. позволяет установить и уровень вероятности, поскольку в таблицах приводятся три значения F теоретического для уровней вероятности 0,95; 0,99; 0,999.

При использовании дисперсионного анализа необходимо соблюдать некоторые правила организации статистических комплексов. В свою очередь, для этого необходимо дать определение основных параметров этих комплексов.

Результативный признак. Результативным признаком называется показатель, изменение которого под влиянием тех или иных условий изучается в эксперименте. В качестве его может приниматься любой признак, характеризующий телосложение, продуктивность или состояние обмена веществ животного.

Подбор факторов. Фактором считается признак, явление или условия, влияние которых на изучаемый признак интересует нас в данном эксперименте. Такими факторами могут быть другие (кроме изучаемого) и не связанные с ним признаки животного, его генотипические особенности, условия внешней среды, кормовые факторы и т. д. В однофакторном комплексе за изучаемый фактор можно принять любой признак.

При организации двух- и многофакторных комплексов выбор факторов для исследования ограничен требованием их полной независимости друг от друга.

Градации факторов. Факторы, подлежащие изучению методом дисперсионного анализа, могут иметь несколько градаций (или уровней). Градации составляют структуру статистического комплекса.

При включении в статистический комплекс двух или трех факторов число градаций по каждому фактору может быть различным. Отсюда следует, что статистические комплексы по своей структуре могут быть более сложными или менее сложными.

По числу включенных в комплекс факторов различают однофакторные, двухфакторные и многофакторные комплексы. В зависимости от соотношений между числом наблюдений в отдельных градациях комплексы могут быть равномерными (ортогональными), пропорциональными и неравномерными. Существуют еще иерархические комплексы, применяемые в статистических исследованиях генетического характера. Техника обработки равномерных и пропорциональных комплексов отличается от обработки неравномерных комплексов.

Ниже приводятся схемы оформления разных типов статистических комплексов. Однофакторный статистический комплекс состоит из нескольких градаций (например, трех) одного фактора.

	A₁	А₂	А₃	г_А = 3
x_i				Sx_i
x_i²				Sx_i²
n_i				Sn = N

Двухфакторный равномерный статистический комплекс состоит из определенного числа градаций по одному фактору (г_А = 2) и внутри них из определенного числа градаций по другому фактору (г_B = 3). Число наблюдений в каждой градации одинаковое.

	A₁			А₂			г_А = 2
	В₁	B₂	B₃	B₁	B₂	B₃	г_B = 3
x_i							Sx_i
x_i²							Sx_i²
n_i							Sn = N

В двухфакторном пропорциональном статистическом комплексе частоты наблюдений в градациях одного фактора (В) пропорционально распределены по градациям другого фактора (А) - в данном примере 1: 2: 3. Техника обработки пропорциональных комплексов не отличается от равномерных, применяемые алгоритмы аналогичны.

	A₁			А₂			г_А = 2
	В₁	B₂	B₃	B₁	B₂	B₃	г_B = 3
x_i							Sx_i
x_i²							Sx_i²
n_i							Sn = N

Различаются еще неравномерные статистические комплексы, техника обработки которых отличается от обработки равномерных и пропорциональных комплексов. В этих комплексах число наблюдений во всех градациях разное и непропорциональное. В неравномерных комплексах утрачивается условие равенства дисперсий, так как при отсутствии ортогональности возникает дополнительный источник дисперсий. Поэтому в этих комплексах

С_Y ¹ С_Z + С_X и ¹ + .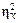

В неравномерных комплексах приходится вычислять специальные поправки на величину С_X.

Подбор особей. Для дисперсионного анализа особи подбираются по принципу случайного отбора, что называется рэндомизацией: random - выбранный наугад (англ.). Организованные таким образом комплексы называются рэндомизированными. Нарушение принципа случайности при отборе в статистический комплекс приводит к неправильным, нерепрезентативным результатам. Отобранные для дисперсионного анализа особи по своим основным показателям должны отражать ту генеральную совокупность, для изучения которой организован эксперимент.

В данном разделе используются некоторые новые термины:

· результативный признак - варьирующий признак, для которого проводится дисперсионный анализ изменчивости, возникающей под влиянием каких-либо факторов;

· варианты результативного признака (X_i);

· организованные (учтенные) факторы (Х-факторы), влияния которых на результативный признак изучаются в данном эксперименте;

· случайные (неучтенные) факторы (Z), действие которых в данном эксперименте является побочным;

· градации или классы, на которые подразделяется в данном эксперименте организованный фактор, воздействующий на результативный признак;

· статистический комплекс - выборочная совокупность, анализируемая методом дисперсионного анализа и организованная по градациям воздействующего фактора;

· дисперсии - общая, факториальная и случайная;

· степени свободы для каждой из полученных дисперсий;

· вариансы (или средние квадраты или взвешенные дисперсии -общая, факториальная и случайная);

· степень изменчивости (или доля изменчивости), обусловленная влиянием фактора (h² - ита квадрат);

· критерий достоверности Фишера (F).

Дисперсионный анализ однофакторных комплексов

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒