
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Техника расчета 3 страница
3. Определяется величина классового промежутка, которая обозначается символом К:
К = 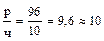 ; К = 10 .
; К = 10 .
4. Определяются границы и середины классов, что видно из таблицы 13. Серединой классов считается полусумма начала данного класса и начала следующего класса или же она равна сумме начала класса и половины классового промежутка.
Таблица 13
| Классы | Отметка числа случаев | Частоты f | |
| границы | середина | ||
| 60 - 69 | 
| ||
| 70 - 79 | 
| ||
| 80 - 89 | 
| ||
| 90 - 99 | 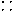 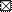
| ||
| 100 -109 | 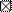 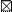 
| ||
| 110 -119 |  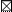
| ||
| 120 -129 | 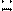 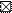
| ||
| 130 -139 | 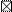 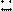
| ||
| 140 -149 | 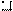
| ||
| 150 -159 | 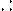
| ||
n = 100
 5. Производится разноска частот. Для этого числа из первичного материала разносятся по соответствующим классам с применением "шифров частот".
5. Производится разноска частот. Для этого числа из первичного материала разносятся по соответствующим классам с применением "шифров частот".
Шифр частот
 |  |
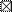


6. Согласно отметке числа случаев по шифру частот проставляют цифровые обозначения частот (f).
В составленном вариационном ряду весь материал приведен в порядок, что позволяет довольно легко проводить расчеты даже для очень многочисленной выборки.
В некоторых случаях внимательное рассмотрение полученного вариационного ряда позволяет получить первое представление об его основных параметрах. Так, в данном случае:
1. Средняя арифметическая должна лежать вблизи 110.
2. Лимиты составляют 60-159 при размахе 100.
3. Среднее квадратическое отклонение по размаху дат 100 : 5 = 20 (ориентировочно).
Составленный вариационный ряд очень удобен для точного расчета необходимых статистических параметров одним из наиболее приемлемых в конкретном случае методов.
 Для расчета средней арифметической и квадратического отклонения применяется способ произведений или способ сумм (эти два способа различаются по технике расчета, условия их применения и получаемые результаты совершенно одинаковы). Целесообразность рассмотрения алгоритмов ручного расчета этими способами определяется тем, что помимо самостоятельного применения они входят в качестве элементов в алгоритмы расчетов других статистических величин. В частности, способ сумм включается в алгоритм расчета коэффициента прямолинейной корреляции по корреляционной решетке, а оба эти способа - в алгоритм расчета корреляционного отношения, характеризующего криволинейные корреляционные связи.
Для расчета средней арифметической и квадратического отклонения применяется способ произведений или способ сумм (эти два способа различаются по технике расчета, условия их применения и получаемые результаты совершенно одинаковы). Целесообразность рассмотрения алгоритмов ручного расчета этими способами определяется тем, что помимо самостоятельного применения они входят в качестве элементов в алгоритмы расчетов других статистических величин. В частности, способ сумм включается в алгоритм расчета коэффициента прямолинейной корреляции по корреляционной решетке, а оба эти способа - в алгоритм расчета корреляционного отношения, характеризующего криволинейные корреляционные связи.
а) Способ произведений (табл.14)
Приведенные формулы расчета средней арифметической X, дисперсии С, квадратического отклонения S и коэффициента вариации V знакомы по предыдущим занятиям. Однако в формулах (1) и (3) есть одна отличительная деталь - в них введен показатель величины классового промежутка. Этот показатель является необходимым элементом при работе с цифровым материалом, сведенным в вариационный ряд.
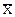
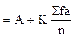 (1); C =
(1); C = 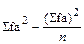 (2);
(2);
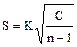 (3);
(3); 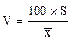 . (4)
. (4)
Таблица 14
| Классы Wa - Ww | Частоты f | Условные отклонения "a" | fa | fa2 |
| 60 - 69 | - 4 | - 16 | ||
| 70 - 79 | - 3 | - 15 | ||
| 80 - 89 | - 2 | - 8 | ||
| 90 - 99 | - 1 | - 14 | ||
| 100 -109 | ||||
| 110 -119 | + 1 | + 12 | ||
| 120 -129 | + 2 | + 30 | ||
| 130 -139 | + 3 | + 45 | ||
| 140 -149 | + 4 | + 24 | ||
| 150 -159 | + 5 | + 15 | ||
| n - 100 | Sfa = 73 | Sfa2 = 517 |
Техника расчета по способу произведений основана на изложенных выше принципах расчета средней арифметической через условную среднюю А. Она слагается из следующих этапов:
1. В составленном вариационном ряду определяется условный средний класс. Лучшим считается тот класс, которому соответствуют наибольшие частоты и который расположен ближе к середине вариационного ряда (эти требования облегчают расчет, но не являются обязательными). Для удобства расчета этот класс отчеркивается горизонтальными линиями. В разбираемом примере это класс 100 -109 с частотой 22.
2. Проставляются условные отклонения "а": кверху от условного среднего класса - отрицательные, книзу - положительные.
3. Рассчитываются произведения условных отклонений на частоты fa и получается их сумма (Sfa) с учетом знаков; Sfa = 73.
4. Рассчитываются произведения частот на квадраты условных отклонений fa2 ; получается сумма Sfa2 = 517.
5. Производится расчет основных параметров по указанным выше формулам.
а) 
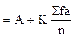 ; А = Wk + ½K = 105, где Wk - начало класса.
; А = Wk + ½K = 105, где Wk - начало класса.

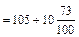 = 105 + 10 ´ 0,73 = 105 + 7,3 = 112,3;
= 105 + 10 ´ 0,73 = 105 + 7,3 = 112,3;  = 112,3
= 112,3
б) с = 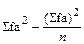 ;
; 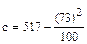 =
= 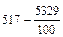 = 517-53,29 = 463,71; с = 463,21
= 517-53,29 = 463,71; с = 463,21
в) 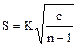 ; S = 10
; S = 10 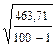 = 10
= 10 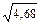 = 21,6
= 21,6
г) 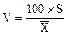
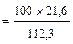 =
= 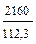 = 19,2; V = 19,2% .
= 19,2; V = 19,2% .
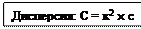 |
Следует обратить внимание, что показатель с =
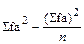 в данном случае является лишь суммой взвешенных квадратов центральных отклонений середин классов от средней ряда, выраженных в квадратах классового промежутка "к". Таким образом, при необходимости расчета дисперсии в данном случае следует использовать формулу:
в данном случае является лишь суммой взвешенных квадратов центральных отклонений середин классов от средней ряда, выраженных в квадратах классового промежутка "к". Таким образом, при необходимости расчета дисперсии в данном случае следует использовать формулу:
В данном примере С = к2 ´ с = 102 ´ 463, 71 = 100 ´ 463, 71 = 46371 .
б) Способ сумм
Метод применяется в тех же случаях, что и предыдущий, т. е. в больших группах при невозможности простого суммирования дат и их квадратов. Как и в предыдущем случае, расчет производится на основе составленного вариационного ряда (в примере изображены стрелки только для удобства усвоения материала, на практике они не применяются).
Таблица 15
| Классы Wa - Wk | Частоты f | P1 = 53 | P2 = 43 |
| 60 - 69 |    4 4
|    4 4
| |
| 70 – 79 |  5 5
|  9 9
| |
| 80 – 89 |   4 4
|  13 13
| |
| 90 – 99 |  14 14
| - | |
| 100 – 109 | - | - | |
| 110 -119 |     12 12
| - | |
| 120 – 129 |  15 15
|   39 39
| |
| 130 – 139 |  15 15
|   24 24
| |
| 140 – 149 |   6 6
|   9 9
| |
| 150 – 159 |  3 3
|  3 3
| |
| n = 100 | q1 = 126 | q2 = 126 |
Применяются формулы:  = А + К
= А + К 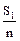 ; S1 = q1 – p1; (S1 = åfa);
; S1 = q1 – p1; (S1 = åfa);
C = 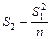 ; S2 = p1 + q1 +2 (p2 + q2); (S2 = åfa2);
; S2 = p1 + q1 +2 (p2 + q2); (S2 = åfa2); 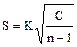
Техника расчета
1. Точно против условного среднего класса проставляют черточки (в первом ряду - одну, во втором - три).
2. Простым суммированием ведется накопление частот от краев к центру до встречи с центральными черточками (по ходу стрелок, проставленных для наглядности). Сначала накапливаются частоты в первом ряду, затем во втором.
3. Определяются суммы накопленных частот р1, q1, p2, q2:
p1 - сумма накопленных частот верхней части первого ряда суммирования, равная 53.
q1 - сумма накопленных частот нижней части первого ряда суммирования, равная 126.
p2 и q2 - то же для второго ряда суммирования, соответственно равные 43 и 126.
4. При расчете данным способом может быть проведена проверка правильности расчета.
Сумма трех чисел - частоты условного среднего класса (22) и чисел, ближних к черточке в первом ряду (27 и 51), должны быть равны числу выборки (n =100). В данном случае: 22+27+51=100.
Сумма двух чисел, ближних к черточкам первого и второго рядов верхней части ряда суммирования, равна числу р1:
22 + 26 = 53
Сумма двух чисел, ближних к черточкам первого и второго рядов нижней части ряда суммирования, равна числу q1:
51 + 75 = 126
5. По полученным величинам р1, р2, q1 и q2 вычисляют две суммы S1 и S2 с учетом знаков. Эти величины только по способу расчета отличаются от основных величин, получаемых при расчете способом произведений. По своей конечной величине S1 = åfa;
S2 = åfa2
S1 = q1 – p1 = 126 – 53 = 73; S1 = 73
S2 = p1 + q1 +2(p2 + q2) =53+126+2 (43+126) =179+2´169 = 179+338 = 517; S2 = 517 .
6. По основным формулам рассчитываются необходимые параметры:
 = A + K
= A + K 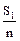 ;
;  = 105 + 10
= 105 + 10  = 105 + 7,3 = 112,3
= 105 + 7,3 = 112,3
C = 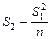 =
= 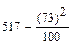 = 517 -
= 517 - 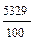 = 463,71
= 463,71
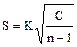 =10
=10 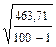 = 10
= 10 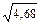 = 21,6 .
= 21,6 .
ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ И ВЫБОРКА. РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕЙ
Весь массив объектов определенной категории, представляющий интерес для исследования, называется генеральной совокупностью. Теоретически - это бесконечно большая или, во всяком случае, приближающаяся к бесконечности совокупность единиц или членов, которые могут быть к ней отнесены. Сущность этого понятия хорошо выражается в испанском языке, на котором "генеральная совокупность" называется словом "universo", что в то же время означает "вселенная".
Обычно генеральная совокупность включает очень большое число объектов: все животные данного биологического вида, поголовье птицы одной породы или одной линии, количество эритроцитов в крови одного животного. Многочисленность составляющих генеральную совокупность единиц в большинстве случаев очень сильно затрудняет или вообще делает невозможным полное ее изучение. В ряде случаев, если поставить задачу полного изучения генеральной совокупности, то потребуется разрушить, уничтожить ее. Так, например, если нужно определить массу яичников у всех кур определенного хозяйства, кур нужно забить, т. е. ликвидировать хозяйство; если требуется изучить состав всей крови животного, придется выпустить всю кровь из организма, т. е. убить животное. Иногда изучаемая совокупность бывает небольшая, в частности, в том случае, если исследователя интересует продуктивность птицы только в одном птичнике, тогда необходимо изучить только 2000-2500 голов птицы.
Сплошное изучение генеральных совокупностей производится редко (перепись населения). Практически же в подавляющем большинстве случаев исследованию подвергается всего лишь часть генеральной совокупности, называемая выборкой. Как правило, выборка - это достаточно небольшая часть генеральной совокупности, но она изучается с целью характеристики всей совокупности. Для достаточно точной характеристики генеральной совокупности параметры выборки должны достаточно правильно соответствовать параметрам генеральной совокупности, т. е. быть репрезентативными (representar - представлять).
Для того, чтобы выборка могла характеризовать генеральную совокупность, следует правильно организовать случайный отбор объектов в эту выборку. При этом совершенно недопустима тенденциозность, предвзятость при выборе объектов, нельзя отбирать только лучшие или только средние объекты, или часть лучших, часть средних и часть худших и т.д. В процессе опыта недопустимо исключать из подопытных групп отдельных особей, почему-либо не устраивающих экспериментатора.
Для получения неискаженной характеристики всей генеральной совокупности необходимо стремиться к тому, чтобы в выборку мог попасть любой объект из любой части генеральной совокупности. В этой связи при выборе объектов для опыта применяется принцип случайности (англ. - sample random test, исп. - al azar).
В зависимости от характера исследования может применяться один из следующих способов отбора объектов в выборку (рассматриваются наиболее употребимые способы):
1. Случайный бесповторный отбор. Объекты для исследования отбираются из генеральной совокупности случайно и обратно в нее не возвращаются. Повторно в выборку попасть не могут. Наиболее распространенный способ отбора из большой, но ограниченной генеральной совокупности. Пример - отбор кур в хозяйстве для вскрытия с целью исследования на гельминты.
2. Случайный повторный отбор. Объекты отбираются в выборку в случайном порядке и после изучения обратно возвращаются в генеральную совокупность. Метод равносилен отбору из бесконечно большой генеральной совокупности. Пример применения - при исследовании развития молодняка птицы случайно отобранной из птичника небольшая партия цыплят взвешивается, после чего цыплята возвращаются в птичник. При повторном взвешивании возможно вторичное попадание отдельных цыплят в случайную выборку.
3. Механический отбор. Отбор объектов из генеральной совокупности производится из отдельных ее частей, которые предварительно намечаются механически по определенной системе. Пример - отбор яиц для анализа по принятой системе из ячеек (по 3, 4 или 6 из каждой ячейки или из части ячеек) в определенном геометрическом порядке. В зависимости от объекта намечается, из скольких частей (ячеек) совокупности отбираются объекты и по сколько образцов (яиц) из каждой части.
4. Серийный гнездовой отбор. В этом случае генеральная совокупность разбивается на части - серии или гнезда. Некоторые серии исследуются целиком и по результатам исследования делается характеристика всей генеральной совокупности. В частности, для получения данных по продуктивности животных в районе можно провести изучение необходимых показателей у всего поголовья в нескольких отдельных хозяйствах. Идеальное осуществление отбора - проведение его методом жеребьевки или же посредством таблицы случайных чисел, позволяющей исключать субъективизм при отборе.
При всяком исследовании есть вероятность допустить ошибки, искажающие истинную картину. Эти ошибки могут быть самого разного характера, однако все их можно подразделить на две основные категории:
А. Категория ошибок, которые можно избежать или свести к минимуму при тщательной организации исследований. К ним относятся:
1) ошибки методического характера, вызванные неправильно избранной методикой исследований;
2) ошибки точности, вызванные употреблением непроверенных измерительных приборов;
3) случайные ошибки, происходящие в результате описок, перепутывания образцов и т. д.;
4) ошибки типичности, обусловленные неправильным, без учета всех условий, отбором объектов в выборку.
Б. Поскольку часть никогда не может полно характеризовать целое, при выборочном исследовании существует особый тип ошибок, вытекающих из самой сущности такого исследования. Таких ошибок избежать невозможно. Они называются ошибками репрезентативности, так как показывают, насколько выборочные параметры отличаются от соответствующих показателей генеральной совокупности, насколько точно они ее представляют, т. е. насколько они репрезентативны. Этих ошибок нельзя избежать, но их можно учесть, и следует стремиться к уменьшению их величины. Существуют способы расчета ошибок этой категории.
Ошибка репрезентативности арифметической средней зависит от двух величин: степени разнообразия признака и численности выборки. Ошибка тем больше, чем выше разнообразие признака. Чем больше численность выборки, тем большая часть генеральной совокупности исследуется и меньше ошибка репрезентативности арифметической средней (рис. 3).
На основе этой закономерности наиболее применимы следующие формулы расчета ошибки репрезентативности средней арифметической:
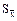 =
= 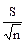 ;
; 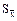 =
= 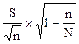
(первая формула применяется при бесконечной генеральной совокупности, вторая - в том случае, если объем генеральной совокупности известен).
Поскольку ошибка прямо пропорциональна изменчивости признака, в числителе формулы стоит среднее квадратическое отклонение (S). Обратная зависимость ошибки от численности выборки отражена тем, что в знаменателе формулы стоит "n".
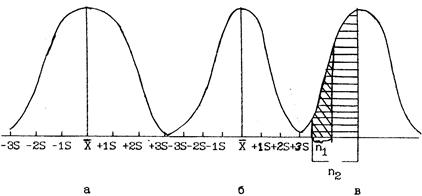
Рис. 3. Зависимость ошибки репрезентативности от разнообразия признака и объекта выборки:
а - распределение признака с высокой вариабельностью; б -распределение признака с низкой вариабельностью; в - небольшая выборка (n1) и большая выборка (n2)
Пример расчета. В качестве примера расчета ошибки средней арифметической можно использовать материалы по массе яиц от группы кур:  = 57,14; S = 4,58; n = 60.
= 57,14; S = 4,58; n = 60.
 =
= 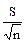 ;
; 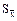 =
= 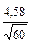 =
= 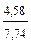 = 0,59;
= 0,59; 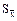 = 0,59
= 0,59
 ±
± 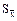 = 57,14 ± 0,59 .
= 57,14 ± 0,59 .
ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ. ТРИ СТЕПЕНИ ВЕРОЯТНОСТИ ПРИ ОПРЕДЕЛЕНИИ ГЕНЕРАЛЬНЫХ ВЕЛИЧИН. КРИТЕРИЙ СТЬЮДЕНТА
В предыдущих разделах отмечалось, что во всяком нормальном распределении в установленных границах значений признака имеется определенная доля дат. Доля дат, ограниченная тем или иным числом средних квадратических отклонений, может быть определена по второй функции нормированного отклонения. Не вдаваясь в подробности рассмотрения этого вопроса, можно отметить, что вторая функция нормированного отклонения определяется по формуле:
j (c) = 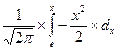 ,
,
где j (c) - обозначение второй функции нормированного отклонения; c- нормированное отклонение заданной величины признака;p = 3,14; е - основание натурального логарифма, равное 2,718. (Нормированное отклонение показывает, на сколько сигм отклоняется значение признака от средней для соответствующей группы.)
Величина j (c), или вторая функция нормированного отклонения указывает ту долю дат, которые находятся между средней арифметической и заданной величиной признака. Значение j (c) или долю дат можно найти по таблице интеграла вероятностей, так что расчет по указанной формуле не всегда обязателен.
В частности, определяем, какая доля дат ограничивается значением одной сигмы (учитывая, что сигма является мерой изменчивости в пределах данного вариационного ряда). Из таблицы интеграла вероятностей следует, что в границах от  до
до  + S имеется 0,341, или 34,1% всех дат данного вариационного ряда. Такое же количество дат находится и в границах
+ S имеется 0,341, или 34,1% всех дат данного вариационного ряда. Такое же количество дат находится и в границах  - S.
- S.
Следовательно, в границах  ± S имеется 0,683, или 68,3% всех дат вариационного ряда. Это значит, что 68,3% всех дат по своему значению не отличаются от средней величины более чем на ±1S. Если примем за границы
± S имеется 0,683, или 68,3% всех дат вариационного ряда. Это значит, что 68,3% всех дат по своему значению не отличаются от средней величины более чем на ±1S. Если примем за границы  ±2S, найдем, что процент дат, отличающихся от средней не более чем на ±2S, равен 2j = 2 0,477 = 0,954, или 95,4%, т. е. в границах от
±2S, найдем, что процент дат, отличающихся от средней не более чем на ±2S, равен 2j = 2 0,477 = 0,954, или 95,4%, т. е. в границах от  - 2S до
- 2S до  + 2S укладывается 95, 4% дат, а за эти пределы выходит только 4-6% дат. При
+ 2S укладывается 95, 4% дат, а за эти пределы выходит только 4-6% дат. При  ± 3S внутри границ окажется 2j-=2 0,4986 = 0,997, или 99, 7% дат, вне этих границ только 0,3% дат.
± 3S внутри границ окажется 2j-=2 0,4986 = 0,997, или 99, 7% дат, вне этих границ только 0,3% дат.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|