
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Техника расчета 6 страница
6. Для дальнейшего расчета решетку можно перечертить, но это важно в случае, если группа очень многочисленна. Если группа сравнительно небольшая, в тех же клеточках вместо условных частот (точек и черточек) можно поставить соответствующие цифры.
Предварительный анализ цифрового материала можно сделать без дальнейших расчетов, на основании изучения вида корреляционной решетки. Это дает возможность установить направление корреляционных связей и сделать первое представление о степени выраженности этих связей. Если основная масса частот располагается вдоль диагональной линии, направленной из левого нижнего угла решетки в правый верхний, т.е. снизу вверх из зоны меньших значений в зону больших значений обоих признаков, то это свидетельствует о наличии прямой или положительной корреляционной связи.
При распределении частот вдоль диагонали, направленной из правого нижнего угла решетки в левый верхний, т.е. из зоны, соответствующей меньшему значению одного и большему значению другого в зону противоположных значений, корреляционная зависимость характеризуется как обратная или отрицательная.
Предварительный вывод о направлении корреляционной связи очень важен, так как это предопределяет выбор схемы расчета и формулы коэффициента корреляции. Предварительный вывод о степени выраженности (или о силе) корреляционой связи может быть сделан по степени концентрации частот вокруг диагональной линии.
При функциональной зависимости частоты располагаются непосредственно на диагонали (полная связь). По мере уменьшения силы связи частоты удаляются от диагонали, их концентрация около диагонали уменьшается пока наконец при отсутствии корреляционной связи они не распространяются равномерно по всей решетке.
Схема степеней прямолинейной корреляции
полная прямая корреляция
r =+1,0
слабая прямая корреляция
r =+0,25
сильная прямая корреляция
r =+0,75
отсутствие
корреляции
r = 0,0
средняя прямая корреляция
r =+0,50
сильная обратная корреляция
r = - 0,75
Предварительный анализ корреляционной решетки в нашем примере позволяет заключить, что между живой массой кур и массой сносимых ими яиц существует прямая (положительная) корреляция, близкая к средней степени.
Расчет коэффициента корреляции по корреляционной решетке
Для проведения расчетов коэффициента корреляции корреляционная решетка несколько усовершенствуется. Линии, разделяющие классы первого признака, продолжаются вниз, а линии, разделяющие классы второго признака, вправо. Это дает возможность построить новые графы для величин n1, n2, p1 и р2, q1 и q2. Вместо границ классов обозначаются их середины (табл. 23).
В настоящем разделе разбирается расчет коэффициента корреляции по способу сумм, являющемуся наиболее удобным при расчетах без использования счетных машин.
Таблица 23
Расчет коэффициента корреляции по корреляционной решетке (положительная корреляция)
| n2 | p1=32 | p2=19 | nd | p1=31 | p2=23 | ||||||||||
| |||||||||||||||
 1 1
| 
| ||||||||||||||
| - | |||||||||||||||

| - | - | - | ||||||||||||
| - | - | - | |||||||||||||
| - | |||||||||||||||
| n1 | q1=23 | q2=11 | |||||||||||||
| q1=21 | - | p1=20 | N = 40 | q1=21 | q2=9 | ||||||||||
| q2=7 | - | - | - | p2=10 | |||||||||||
Таблица вспомогательных величин
| S1=p1-q1 | S2=p1+q1+2(p2+q2) | S12 | 
| C = S2- 
|  =A+K =A+K 
| S=K 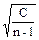
| |
| 20-21=-1 | 20+23+2(10+7)=75 | -1 | 0,025 | 75-0,025=74,975 | 1675+50´ 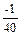 =1673,75 =1673,75
| 50´  =70 =70
| |
| 32-23=9 | 32+23+2(19+11)=115 | 2,025 | 115-2,025=112,975 | 56+1´ 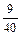 =56,12 =56,12
| 1´ 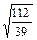 =1,7 =1,7
| ||
| d | 31-21=10 | 31+21+2(23+9)=116 | 2,50 | 116-2,50=113,50 | - | - |
Основной формулой, применяемой в этих расчетах, является
r = 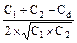 ,
,
где С1 = 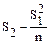 .
.
В свою очередь, S1 = p1 - q1; S2 = p1 + q1+2(p2 + q2), как и при расчете среднего квадратического отклонения методом сумм. Расчет производится в следующем порядке:
1. По каждому признаку (первому и второму) в классах производится суммирование частот, полученные суммы заполняют клеточки в графах n1 (первый признак) и n2 (второй признак). Общая сумма частот по горизонтали должна быть такой же, что и по вертикали, она равна объему выборки N (в нашем примере 40).
2. Проводится накопление частот методом суммирования сначала по графам первого признака (горизонтальным), а затем по графам второго признака (вертикальным). Средняя черточка, определяющая условный средний класс, ставится в графе первого порядка (р1 – q1) против середины класса или против класса с наибольшим числом частот. Используется тот же порядок, что и при расчете методом сумм. В графе порядка (p2 – q2) проставляются черточки и частоты накапливаются также суммированием.
3. Проставляются суммы накопленных частот первого (р1, q1) и второго (р2, q2) порядков как по первому, так и по второму ряду признаков. После этого приступают к накоплению частот по ряду разностей.
4. В корреляционной решетке определяется средняя клеточка частот. За среднюю клетку принимается та, которая находится на пересечении условных средних первого и второго признаков. Цифра в этой клеточке выделяется квадратиком. Она является нулевой разностью, условной средней для ряда разностей.
5. На корреляционной решетке проводятся диагональные линии, на которые как бы нанизываются частоты.
6. Вдоль этих диагональных линий суммируются частоты ряда разностей. Полученные суммы проставляют в клеточки графы nd.
При положительной корреляции диагонали проходят из левого нижнего угла в правый верхний угол решетки, при отрицательной корреляции - наоборот.
7. Сумма частот, полученная накоплением частот вдоль диагонали, проходящей через отмеченную квадратиком среднюю клетку, принимается за средний класс в ряду разностей. Это очень важное правило, отступление от которого не допускается.
Против этого класса ставятся одна черточка в ряду первого порядка и три черточки в ряду второго порядка. Производится накопление частот суммированием, после чего проставляются суммы первого (р1 и q1) и второго (р2 и q2) порядков.
В дальнейшем все расчеты можно начинать с определения центральной клетки в месте наибольшего скопления частот и недалеко от геометрического центра решетки. Тогда условно средние классы в рядах первого и второго признаков определяются в зависимости от положения центра клетки.
8. По каждому ряду признаков (первый признак, второй признак и ряд разностей) рассчитываются вспомогательные величины S1, S2 и С по известным формулам, так же как и при вычислении среднего квадратического отклонения. Полученные результаты записываются в таблицу вспомогательных величин. В этой же таблице можно рассчитать и записать значения средней арифметической и квадратического отклонения для первого и второго признаков.
9. Для уточнения правильности расчетов проводится проверка. Первоначально в ряду каждого признака и в ряду разностей проводится проверка, аналогичная той, которая применялась в методе сумм:
а) сумма трех цифр (частоты в условном среднем классе и двух накопленных частот в ряду первого признака, лежащих около черточки) равна объему выборки;
б) сумма двух цифр, лежащих около черточек накопленных частот первого и второго порядков (отрицательные), равна числу q1.
Сумма двух аналогичных положительных частот равна р1.
Если все последующие вычисления сделаны верно, то должно соблюдаться равенство: S1(2) – S1(1) = S1(d), т.е. разница между первой вспомогательной суммой второго ряда и первой вспомогательной суммой первого ряда равна первой вспомогательной сумме по ряду разностей.
10. Получив значение дисперсий, выраженных в квадратах классового промежутка для первого и второго признаков – С1 и С2 , а также аналогичную величину по ряду разностей - Сd, вставляют их в формулу для расчета коэффициента корреляции:
r = 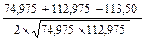 =
= 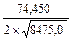 =
= 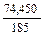 =0,402; r=+0,402 .
=0,402; r=+0,402 .
Таким образом, получена положительная корреляция при r=+0,40 . Рассмотренный способ расчета наиболее удобен при положительной' корреляции между признаками.
Если приходится иметь дело с обратной, отрицательной корреляцией, проще использовать не разности, а суммы отклонений, а расчет коэффициента корреляции вести по формуле:
Таблица 24
Расчет коэффициента корреляции по корреляционной решетке (отрицательная корреляция)
| 86 -90 | 91 -95 | 96 – 100 |  101 – 105 101 – 105
|  106 – 110 106 – 110
| 111 – 115 | 116 – 120 | n2 | p1=24 | p2=9 | nS | p1=17 | p2=6 | |||
  1 1
|  2 2
|  3 3
| |||||||||||||
| - | |||||||||||||||
  1 1
|
| - | - | - | |||||||||||
| - | - | - | |||||||||||||
| - | |||||||||||||||
| n1 | q1=37 | q2=30 | |||||||||||||
| q1=27 | - | p1=15 | N = 40 | q1=42 | q2=32 | ||||||||||
| q2=16 | - | - | - | p2=5 | |||||||||||
Таблица вспомогательных величин
| S1=p1-q1 | S2=p1+q1+2(p2+q2) | S12 | 
| C = S2- 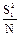
| 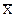 =A+K =A+K 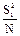
| S=K 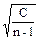
| |
| 15-27=-12 | 15+27+2(5+16)=84 | 3,6 | 84-3,6=80,4 | 103,5+5 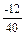 =102 =102
| 5´ 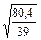 =7,0 =7,0
| ||
| 24-37=-13 | 24+37+2(9+30)=139 | 4,2 | 139-4,2=134,8 | 57+1´ 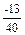 =56,68 =56,68
| 1´ 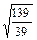 =1,94 =1,94
| ||
| S | 17-42=-25 | 17+42+2(6+32)=135 | 15,6 | 135-15,6=119,4 | - | - |
r = 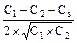 .
.
Направление корреляции можно определить по виду распределения частот сразу после заполнения корреляционной решетки (об этом говорилось выше). При отрицательной корреляции для получения ряда сумм отклонений частоты суммируются по диагоналям, проходящим из правого нижнего угла решетки в левый верхний угол (т.е. перпендикулярно диагоналям при положительной корреляции).
В следующем алгоритме (табл.24) приводится пример расчета корреляции между яйценоскостью кур за 5 месяцев продуктивности и средней массой сносимых ими яиц.
1- признак - яйценоскость за 5 мес. продуктивности кур
2-й признак - средняя масса яиц (г).
Как видно по корреляционной решетке (табл. 24), в данном случае имеет место отрицательная корреляция и расчет проводится в соответствии с этим. Расчет примера в алгоритме показал, что между указанными признаками кур существует отрицательная корреляция при r = -0,83:
r= 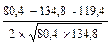 =
= 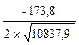 =
= 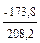 = -0,83 .
= -0,83 .
Ошибка коэффициента прямолинейной корреляции и достоверность коэффициента корреляции
Поскольку коэффициент корреляции рассчитывается как величина, характеризующая определенную выборку, он имеет свою ошибку репрезентативности.
Для больших выборок эта ошибка рассчитывается по формуле:
Sr = 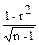 ,
,
где r - коэффициент корреляции генеральной совокупности; n - число пар значений в выборке, т. е. ее объем. В эту формулу включается коэффициент корреляции для генеральной совокупности, который в практической работе известен исключительно редко. Вследствие этого в большинстве исследований вместо точного значения ошибки коэффициента корреляции берут ее приближенное значение, которое может быть определено по формуле с включением выборочного коэффициента корреляции:
Sr = 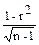 .
.
Необходимо отметить, что эта формула расчета ошибки коэффициента корреляции действительна лишь для больших выборок, когда число пар в выборке не меньше 100. При работе с малыми выборками (n<100) расчет по этой формуле дает менее точные, а иногда и совсем неверные результаты. В этой связи при п<100 применяется другая формула ошибки коэффициента корреляции:
Sr = 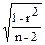 .
.
Для определения достоверности выборочного коэффициента корреляции рассчитывается критерий достоверности:
tr = 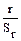 =r´
=r´ 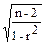 .
.
Рассчитанный критерий tr оценивается так же, как и критерий достоверности разности средних или долей, т.е. путем сравнения полученного значения t с фиксированными значениями по таблице Стьюдента (в соответствии с тремя степенями безошибочных суждений). При этом число степеней свободы принимается равным числу пар определений минус 2, т.е. n = n-2. В качестве упражнения рассчитываем ошибку и достоверность коэффициента корреляции на материале примеров, рассмотренных ранее.
1. В расчете получен коэффициент корреляции г - +0. 31 при n = 10:
Sr = 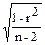 ; Sr =
; Sr = 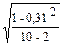 =
= 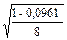 =
= 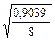 =
= 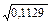 = 0,336 Sr = 0,336
= 0,336 Sr = 0,336
tr = 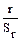 ; tr =
; tr = 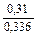 =0,92; tr = 0,92
=0,92; tr = 0,92
n = 10-2=8; tst = 2,3 – 3,4 – 5,0; tr = 0,92 < tst (при P<0,95).
Коэффициент корреляции в данном случае оказался недостоверным.
2. В одном из расчетов был использован аналогичный материал, что и в предыдущей задаче, но взят больший объем выборки. Получены данные: r= +0,40 при n =- 40:
Sr = 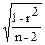 ; Sr =
; Sr = 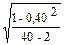 =
= 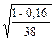 =
= 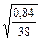 =
= 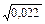 = 0,148 Sr = 0,148
= 0,148 Sr = 0,148
tr = 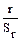 ; tr =
; tr = 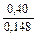 =2,7; tr = 2,7
=2,7; tr = 2,7
n = 40-2=38; tst = 2,5 – 2,7 – 3,6; tr=2,7 = tst (при P<0,99).
Коэффициент корреляции (r = 0,40) достоверен при втором уровне вероятности безошибочного суждения.
В первом случае коэффициент корреляции получился недостоверным в силу недостаточного объема выборки. Увеличение числа измерений до 40 пар во втором случае позволило получить достоверный коэффициент корреляции.
Если в исследовании важно определить только достоверность коэффициента корреляции, а ошибка коэффициента не представляет интереса, расчет может быть значительно упрощен.
В таблице 25 приведены значения объема выборки n при возможных значениях коэффициента корреляции. Использование таблицы делает очень простым определение достоверности коэффициента корреляции - при этом отпадает необходимость в вычислениях. Таблица применима для работы с выборками любой численности, как большими, так и малыми.
Таблица 25
Количество пар значений, достаточное для достоверности выборочного коэффициента прямолинейной корреляции (n)
| r | n | ||
| P1=0,95 | P2=0,99 | P3=0,999 | |
| t1=1,96 | t2=2,58 | t3=3,30 | |
| .01 | |||
| .02 | |||
| .03 | |||
| .04 | |||
| .05 | |||
| .06 | |||
| .07 | |||
| .08 | |||
| .09 | |||
| .10 | |||
| .11 | |||
| .12 | |||
| .13 | |||
| .14 | |||
| .15 | |||
| .16 | |||
| .17 | |||
| .18 | |||
| .19 | |||
| .20 | |||
| .21 | |||
| .22 | |||
| .23 | |||
| .24 | |||
| .25 | |||
Продолжение табл.25
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|