Техника расчета 12 страница

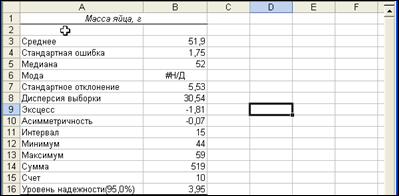
Рис.7. Результаты Описательной статистики

Для форматирования таблицы с выходными данными (изменения ширины столбца и разрядности отображения чисел ) используйте стандартный набор действий, принятый в пакете Microsoft Office.

Интерпретация результатов

Выходные данные содержат три показателя общей направленности: среднее, медиана и мода.

Средняя масса яйца в выборке - 51,9 г, получившаяся в результате деления Суммы (519) на Счет (10).

Медиана (термин был впервые введен Гальтоном, 1882 г.) - это значение, которое разбивает выборку на две равные части. Половина наблюдений лежит ниже медианы и половина наблюдений - выше медианы. Медиана равна 52 г. Таким образом, примерно половина яиц имеет массу, большую 52 г, и примерно половина меньший показатель. Для нечетного числа данных n медианой является значение с рангом (n + 1)/2, а для четного медиана располагается ровно между двумя значениями с рангами n/2 и n/2 + 1.

Мода – показывает значение, которое наиболее часто встречается в совокупности. Когда имеется несколько значений, повторяющихся одинаковое число раз (несколько мод), то Excel использует значение, появившееся ранее всего в данных. Если каждое значение встречается только один раз и является модой, Excel в соответствующей строчке оставляет «#Н/Д».

В таблице выходных данных имеется несколько характеристик дисперсии. Интервал (15 г) определяется как разность Максимума (59 г) и Минимума (44 г) (в первой части пособия называется лимит). Как было сказано выше, для некоторых наборов данных интервал может быть недостаточно хорошей характеристикой дисперсии, так как он основан только на двух экстремальных значениях, которые могут быть нехарактерными для выборки.

Стандартное отклонение (среднее квадратическое отклонение) (5,53 г) - наиболее широко используемая характеристика изменения данных. Вычисляется по формуле: 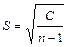. Стандартное отклонение измеряется в тех же единицах, что и исходные данные, т. е. граммы в нашем примере.

Дисперсия – в данном случае необходимо отметить, что выражение "дисперсия", принятое при расчете в Excel, соответствует значению "варианса" или "средний квадрат", принятому в практикуме (см. раздел "Варьирование признаков. Показатели вариабельности"), выражается в единицах в квадрате: грамм². То, что в выходной таблице называется стандартным отклонением и дисперсией, на самом деле является выборочным стандартным отклонением и выборочной дисперсией, вычисляемыми с (n— 1) в знаменателе.

Стандартная ошибка (ошибка репрезентативности) среднего (1,75 г) равняется выборочному стандартному отклонению, поделенному на корень квадратный из размера выборки. Стандартная ошибка является характеристикой достоверности среднего и используется в статистических выводах (доверительные интервалы и проверки гипотез).

Уровень надежности (95,0%) (3,95 г) равняется половине длины 95% доверительного интервала для среднего. Указанный уровень надежности 95% соответствует t = 2,26 (≈ 2,3) для t-распределения (распределения Стьюдента) с суммарной мерой двух хвостов 5% и n - 1 = 10 - 1 = 9 степенями свободы. Половина длины доверительного интервала вычисляется как t, умноженное на стандартную ошибку, т. е. 2,26 умножить на 1,75 г или 3,95 г.

Левая граница девяностопятипроцентного доверительного интервала равна среднему минус половина ширины, а правая — среднему плюс половина ширины, т. е. 51,9 – 1,75 и 51,9 + 1,75 соответственно, или приближенно от 50,15 до 53,65 г.

Эксцесс является показателем островершинности симметричных распределений. Если распределение более плоское, чем нормальное, т. е. имеет более «тяжелые» хвосты по сравнению с нормальным распределением, то эксцесс будет положительным. Если же распределение имеет более выраженный пик, чем нормальное, т. е. имеет более «легкие» хвосты, то эксцесс отрицательный. В нашем примере распределение примерно симметричное с отрицательным эксцессом (-1,817). (Excel вычисляет эксцесс, используя четвертую степень отклонений от среднего. За подробностями обратитесь к разделу Справки «ЭКСЦЕСС».)

Асимметричность показывает степень симметрии распределения. Говорят, что распределение имеет положительное отклонение, или скошено вправо, если большинство экстремальных значений расположены в положительном направлении. Если же большинство экстремальных значений расположено в отрицательном направлении, то распределение имеет отрицательное отклонение, или скошено влево. В противном случае распределение симметрично или приближенно симметрично. В нашем примере асимметричность слабо отрицательна (-0,07). (Excel вычисляет эксцесс, используя третью степень отклонений от среднего. За подробностями обратитесь к разделу Справки «СКОС».)

ИНСТРУМЕНТ АНАЛИЗА: ГИСТОГРАММА

Инструмент анализа Гистограмма строит таблицу распределения частот данных и на ее основе создает диаграмму. В результаты кроме отдельных частот могут быть включены интегральные проценты.

Перед использованием инструмента следует определить классовые промежутки. В противном случае Excel использует равные интервалы количеством, приближенно равным квадратному корню из числа значений данных, начиная с минимального и заканчивая максимальным значением. В случае четко заданных интервалов лучше использовать числа, кратные двойке, пятерке или десятке для облегчения анализа.

Чтобы определить интервалы, сначала найдите минимальное и максимальное значения данных с помощью Описательной статистики. Используйте полученные величины для определения промежутка, который будут занимать интервалы гистограммы. Обычно бывает достаточно от 5 до 15 интервалов. Максимальное значение для каждого интервала в Excel называется карманом. Инструмент Excel автоматически добавляет интервал, называемый Еще, к уже указанным карманам и в который будут входить максимальные значения.

Так как в нашем примере численность выборки небольшая, то можно предоставить Excel автоматически определить классовые промежутки.

Выполните следующие шаги для получения распределения частот и гистограммы:

1. В меню Данные выполните команду Анализ данных и выберите инструмент Гистограмма в списке доступных инструментов (рис.8).

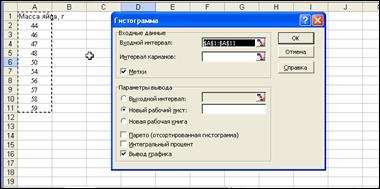
Рис.8. Диалоговое окно гистограммы

2. Входной интервал:введите ссылки на ячейки с данными (А1:А11),включая метку (не забудьте включить опцию "Метки").

3. Выходной интервал:введите ссылку для левого верхнего угла области, если хотите расположить таблицу выходных данных на текущем листе. Таблица вместе с диаграммой занимает примерно десять столбцов. В данном случае будем формировать выходные данные в новом рабочем листе.

4. Парето (отсортированная диаграмма): при включении данного пункта интервалы сортируются в соответствии с частотами перед отображение диаграммы (в нашем примере опция отключена).

5. Интегральный процент: включите данную опцию для получения интегрального процента вдобавок к отдельным частотам (в нашем примере опция отключена).

6. Ввод графика: отметьте этот пункт для получения не только таблицы распределения частот, но и диаграммы на листе (в нашем примере опция включена).

7.По окончании заполнения полей окна нажмите "ОК".

Excel разместит таблицу распределения частот и гистограмму на новом листе (рис.9).

Значения карманов являются правыми границами интервалов.

Например, интервал, соответствующий карману со значением 49, включает значения, строго большие 44 (предыдущий карман) и меньшие либо равные 54. В данный карман попали три значения: 46, 47 и 48 грамм.

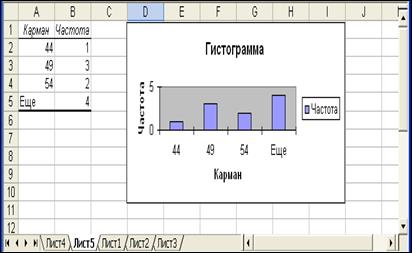
Рис.9. Таблица частот и гистограмма

Усовершенствование гистограммы

Чтобы диаграмма была более похожа на обычные гистограммы и удобочитаема, можно произвести следующие изменения.

1.Легенда:если на диаграмме изображен только один набор данных, в обозначениях нет необходимости. В противном случае щелкните по легенде («Частота» справа от диаграммы) и нажмите клавишу Delete, чтобы удалить. При этом увеличится поле, где размещается собственно диаграмма.

2. Формат области диаграммы:областью диаграммы называется прямоугольная область, ограниченная осями X и Y (в данном случае выделена серым цветом). Дважды щелкните по ней (над столбцами) и в окне Формат Области Построения установите Нет заливки, а выбрав Цвет границы установить нет линий.

3. Подписи по осиY: если вы измените высоту диаграммы, то могут появиться на оси Y промежуточные значения (0,5, 1,5,...), но частоты должны быть целыми числами. Дважды щелкните по оси Y (оси значений); в окне Формат оси на вкладке Параметры оси установите Цену основного деления и Цену промежуточных делений, равными целому числу (в данном случае 1). Нажмите ОК.

4. Ширина столбцов:в обычных гистограммах столбцы не разделены, а находятся рядом. Дважды щелкните по одному из столбцов (при этом все столбики должны стать помеченными знаком выделения); в появившемся окне Формат ряда данных на вкладке Параметры ряда измените Ширину бокового зазора со 150% на 30%. Нажмите ОК.

5. Подписи по оси X: дважды щелкните по оси X (ось категорий); в окне Формат Оси на вкладке Выравнивание выберите Направление текста Горизонтально. Тогда при любом изменении размеров диаграммы подписи на оси X будут горизонтальными. Нажмите ОК.

6. Название диаграммы:дважды щелкните по тексту Гистограмма (название диаграммы) с интервалом 1-2 секунды. Напечатайте Масса яйца, г и нажмите Enter. В основном меню выберите пункт Формат и измените стиль шрифта. Если диаграмма построена по данным нескольких признаков (столбиков) или заголовок состоит из большого количества символов, то лучше название не вводить, так как это приведет к уменьшению области построения собственно диаграммы. В этом случае название вводится отдельно в текстовом редакторе и вставляется перед диаграммой. Слово "Гистограмма" в этом случае выделяется двойным щелчком и удаляется нажатием клавиши Delete.

7. Название оси Y: дважды щелкните по названию оси значений Частота с интервалом 1-2 секунды. В основном меню выберите пункт Формат и измените стиль шрифта.

8. Название оси X: щелкните по слову «Карман». Введите Максимум интервала, в г.Изменитестиль шрифта как в предыдущих абзацах. Excel размещает значения по оси X в серединах интервалов, а не у отметок, разделяющих их. Данный заголовок поясняет читателю, что данные значения являются максимальными для соответствующего интервала.

9. Цвет столбцов:столбцы темного цвета при печати могут выглядеть черными, без просветов, так что бывает трудно разглядеть их границы. Щелкните в центре одного из столбцов (при этом все столбики должны стать помеченными знаком выделения), чтобы выбрать ряд данных. Щелкните правой кнопкой мыши, выберите Формат ряда данных и перейдя на вкладки Заливка и Цвет границы измените параметры цветового оформления. Нажмите ОК.

Для перемещения диаграммы щелкните где-нибудь внутри границы (по области диаграммы) и перетяните гистограмму в нужное место. Для изменения размеров сначала щелкните по области диаграммы, а затем перетяните один из восьми появившихся черных маркеров. В результате получим диаграмму, показанную на рис. 10.

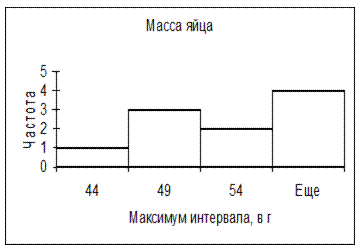
Рис.10. Усовершенствованная гистограмма

ИНСТРУМЕНТ АНАЛИЗА: РАНГ И ПЕРСЕНТИЛЬ

Инструмент анализа Ранг и персентиль создает таблицу, содержащую порядковые ранги и персентили для каждого значения данных. На рис. 11 показаны параметры диалогового окна инструмента анализа в применении к данным о массе яйца, а на рис. 12 представлены результаты Ранга и персентиля.

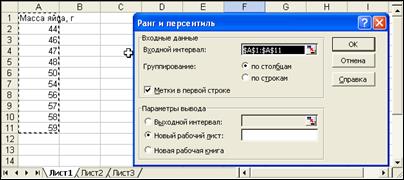
Рис.11. Диалоговое окно инструмента Ранг и персентиль

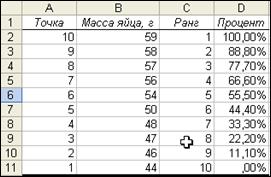
Рис.12. Результаты инструмента Ранг и персентиль

Значения персентиля в столбце D соответствуют 100% для максимального значения и 0% для минимального. Промежуточные значения имеют персентили, расположенные с шагом 1/(n - 1), где п - число наблюдений.

ОЦЕНКА СРЕДНИХ ДВУХ ВЫБОРОК

В данном разделе описываются средства сравнения средних двух выборок. Рассматривается два подхода, использующих выборочные стандартные отклонения от оценки стандартных отклонений совокупностей с применением распределения Стьюдента.

Случай равных дисперсий. Распределение Стьюдента

Вдобавок к предположениям о нормальности, независимости и случайности выборок данный критерий также предполагает возможное равенство дисперсий совокупностей (этот метод был положен в основу расчетов достоверности разности средних арифметических в первой части пособия).

Рассмотрим следующий пример.Имеются данные по массе яиц кур, полученные в одном из экспериментов.

1-я группа, г					2-я группа, г
58,5	59,9	61,1	58,7	56,6	59,4	54,0	57,5	47,0	50,0
58,7	53,5	56,8	56,1	48,8	50,0	45,0	56,6	50,6	55,9
54,0	56,7	50,2	60,5	55,0	54,4	60,2	51,0	60,6	61,0
64,5	60,2	59,9	61,6	62,7	60,0	52,0	52,2	53,0	52,0

Требуется определить, различаются ли группы по средней массе яиц?

Следующие действия описывают, как проверить гипотезу равенства средних.

1. Внесите данные в таблицу Excell в столбики A и B.

2. В меню Данные выберите Анализ данных, внизу списка Инструменты анализа выберите Двухвыборочный t-тест с одинаковыми дисперсиями. Затем нажмите ОК. Появится диалоговое окно, как на рис. 13.

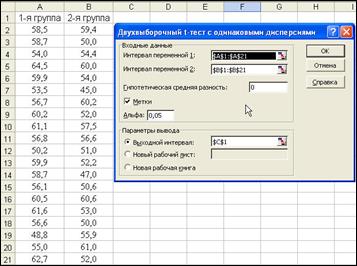
Рис. 13. Диалоговое окно критерия при одинаковых дисперсиях

3. Укажите мышкой на листе ячейки с данными и меткой "1-я группа" в строке Интервал переменной 1 или введите A1:A21.Для Интервала переменной 2 выделите данные под меткой "2-я группа" или введите B1:B21.

4. Введите 0 в строку Гипотетическая средняя разность, отметьте пункт Метки и введите 0,05для Альфа (уровень значимости P=0,95).

5. В данном случае будем выводить данные в текущем листе Excel, поэтому щелкните по кнопке Выходной интервал, выделите соответствующую строку ввода и укажите на ячейку С1 листа ($C$1) (левый верхний угол). Затем нажмите ОК.

6. Чтобы уменьшить количество десятичных знаков для нецелых чисел, выделите сначала ячейки D5:E5, затем, удерживая нажатой клавишу Ctrl, D7 и D10:D14, щелкните несколько раз по кнопке Уменьшить разрядность, пока не останется только два десятичных знака.

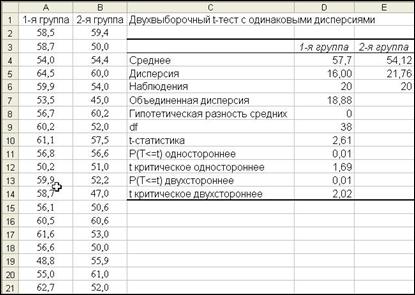
Рис. 14. Результаты проверки гипотезы

Объединенная дисперсия - это взвешенное среднее выборочных дисперсий со степенями свободы каждой выборки в качестве весов. Она является оценкой общей дисперсии двух совокупностей и используется для определения стандартной ошибки разности средних, не представленной в результатах.

df - это число степеней свободы критерия, равное сумме размеров выборок минус два (n₁ + n₂ - 2).

t-статистика вычисляется как отношение разности выборочных средних минус предполагаемая разность средних к стандартной ошибке. (В данном случае это есть ни что иное, как фактический критерий достоверности разности t_d, который был описан в первой части пособия в разделе "Доверительная вероятность. Три степени вероятности при определении генеральных величин. Критерий Стьюдента".)

Р(Т <= t) одностороннее является односторонним р-значением и зависит от вычисленных значений t и df. Если t отрицательно, то одностороннее р-значение равно Р(Т <=t); если же t положительно, то фактически р-значение равно Р(Т >= t). На рис. 14 р-значение показывает, что в случае, когда нулевая гипотеза справедлива, то есть средние совокупностей равны, вероятность получить разницу выборочных средних не меньше измеренной равна 0,01. р-значения используются при применении подхода с выводом р-значения к проверке гипотезы.

Р(Т <= t) двустороннее - двустороннее р-значение, равное удвоенному одностороннему р-значению. Если нулевая гипотеза справедлива, то данное значение равно вероятности получить измеренную разность выборочных средних в любом направлении.

t критическое одностороннее и t критическое двустороннее зависят от параметра альфа (уровня значимости), указанного в диалоговом окне и df.

В рассматриваемом примере спрашивается, различаются ли средние, следовательно, нужно применить двусторонний критерий.

Двустороннее критическое значение t в первой части пособия определялось как стандартное значение критерия Стьюдента (t_st) по табл. 17. В данном примере значение t_d (t- статистика), равное 2,61, больше, чем значение t_st (t критическое двустороннее), т.е. 2,61>2,02. Это означает, что нулевая гипотеза отвергается, и разность между средними (57,7 – 54,12 = 3,58) статистически достоверна. Следовательно, яйца, составляющие 1-ю группу, имеют в среднем более крупную массу по сравнению с яйцами, отобранными во 2-ю группу.

Доверительный интервал

Используйте следующие инструкции, чтобы построить доверительный интервал для разности средних.

1. Введите метки (текст в ячейках) в столбец G, как показано на рис. 15.

2. Введите формулы в столбец H, как на рис. 15. Первый аргумент функции СТЬЮДРАСПОБР в ячейке H6 должен быть равен единице минус уровень значимости (т.е. для 95% уровня 1-0,95=0,05). Для получения 99% доверительного интервала вместо 95% замените 0,05 на 0,01. По мере введения формул будет производиться автоматический расчет данных.

3. После того как введены все формулы, выделите ячейки H4:H9 и щелкните по кнопке Уменьшить разрядность на панели инструментов, чтобы получить формат чисел, как на рис. 16.

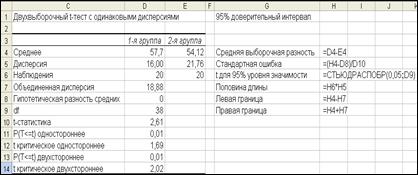
Рис. 15. Формулы для построения доверительного интервала

при равенстве дисперсий

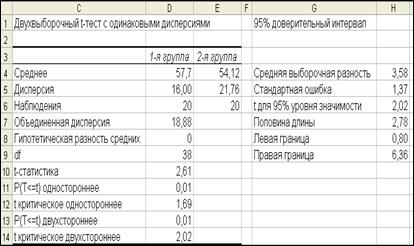
Рис. 16. Доверительный интервал при равенстве дисперсий

Измеренные средняя разность и стандартная ошибка, показанные в столбце H, необходимы не только для вычисления доверительного интервала, но и для интерпретации статистики t, которая получается в результате деления разности выборочных средних минус разность предполагаемых средних на стандартную ошибку, то есть в данном случае 2,61 равно (3,58-0)/1,37).

Доверительный интервал допускает следующую интерпретацию: с 95% вероятностью разность средних совокупности находится между 0,80 и 6,36.

ПАРНЫЕ ВЫБОРКИ. РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА

Парный выборочный критерий используется в случае, когда одна и та же группа показателей наблюдается дважды. Обычно это происходит при измерениях характеристик до и после некоторого вмешательства. Например, физиологические показатели крови животных могут тестироваться до и после курса лечения. В данных случаях выборки не являются независимыми.

Критерий также может использоваться, когда имеются другие естественные пары измерений, связанные каким либо способом друг с другом, то есть когда отменяется предположение о независимости выборок.

Пример. Исследователь хочет определить, имеется ли разница в живой массе свиней, взвешенных до и после транспортировки на мясокомбинат. Для этого выбрали случайным методом восемь животных и взвесили. Получены следующие данные:

Масса до транспортировки, кг (А)
Масса после транспортировки, кг (Б)

Можно ли заключить с уровнем значимости 95%, что животные, взвешенные в разные временные отрезки, существенно различаются по живой массе?

Введем данные в таблицу Excel (рис.17).

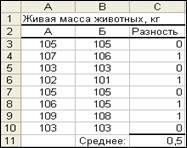
Рис.17. Парная выборка данных

Так как данные расположены по парам, мы будем исследовать среднее попарных разностей, приведенных в столбце C (см.рис. 17). В ячейку C3 была введена формула =AЗ-B3, затем она была скопирована и вставлена в ячейки C4:C10. Ячейка C11 содержит формулу =CP3HAЧ(С3:С10).

Проверка гипотезы

Нулевая гипотеза состоит в том, что разность средних совокупностей равна нулю, а альтернатива - разность средних совокупностей не равна нулю. Поэтому воспользуемся двусторонним критерием. Если полученная разность средних (0,5 кг) не типична для выборки из совокупности с разностью средних ноль, мы можем отвергнуть нулевую гипотезу и заключить, что животные имели разную массу до и после транспортировки.

Для проверки нулевой гипотезы, что разность средних совокупностей равна нулю, выберите в меню Данные последовательно Анализ Данных, Парный двухвыборочный t-тест для средних и нажмите ОК. Заполните строки ввода диалогового окна в соответствии с рис. 18.

Рис. 18. Диалоговое окно парных выборок

После изменения ширины столбцов и числа десятичных знаков результат показан на рис. 19.

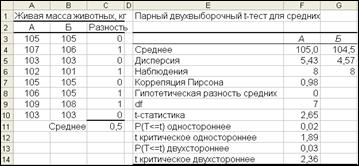
Рис. 19.Парные выборки данных и результаты анализа

Результаты инструмента анализа, представленные на рис. 19, подобны тем, что мы видели при выполнении других t-критериев, за исключением того, что включен коэффициент корреляции Пирсона.

При подходе с принятием решения для данного двустороннего критерия мы можем отвергнуть нулевую гипотезу, если t-статистика (2,65) больше его, взятого со знаком плюс (+2,36). Статистика t в данном примере оказалась больше двустороннего критерия, поэтому мы можем отвергнуть нулевую гипотезу. Таким образом, существует достаточно оснований заключить, что свиньи имеют разную массу при первом и втором взвешивании, то есть в данном случае во время транспортировки каждое животное в среднем потеряло 0,5 кг .

Доверительный интервал

На рис. 20 в столбце М показаны формулы для вычисления доверительного интервала. Данные формулы подобны тем, что приведены на рис. 15, хотя некоторые ссылки отличаются.

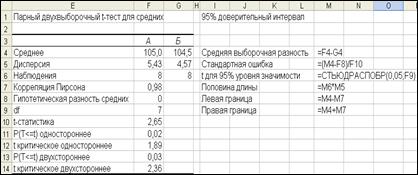
Рис. 20. Формулы доверительного интервала для парных выборок

На рис. 21 приведены результаты вычислений доверительного интервала. Интерпретация результатов следующая: с вероятностью 95% разность средних совокупностей находится между 0,1 и 0,9 кг, или потери массы каждым животным за время транспортировки колеблются в пределах от 100 до 900 г. Лучшей оценкой действительной разницы является число, полученное на основе выборки (ячейка М4), которое показывает, что средняя живая масса животных при первом взвешивании была на 0,5 кг больше, чем при втором взвешивании.

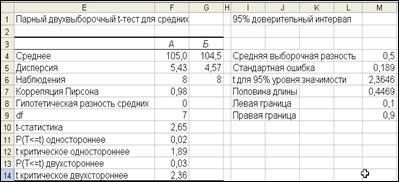
Рис. 21. Результаты построения доверительного интервала

ДВУМЕРНЫЕ ЧИСЛОВЫЕ ДАННЫЕ

Для изучения зависимости между двумя числовыми переменными используются графики рассеяния. В Excel данный вид графиков называется точечной диаграммой; его также называют диаграммой рассеяния или XY-графиком. Такое графическое представление часто является первым шагом в процедуре приближения данных кривой с помощью регрессионной модели.

Пример 1. Данные, представленные на рис. 22, были взяты из табл.21 первой части пособия. 1-й признак - число яиц, снесенных 10 курами за 10 дней; 2-й признак - число яиц, снесенных за те же 10 дней их дочерьми.

При сравнении двумерных массивов считается, что он состоит из двух переменных (двух признаков), одна из которых называется зависимой переменной, а другая – казуальной переменной. Иногда зависимую переменную называют откликом или У-переменной. Аналогично, казуальную переменную называют независимой переменной или Х-переменной.

Наша первоначальная цель - визуально исследовать зависимость между яйценоскостью кур матерей и дочерей. Затем вычислить общую характеристику - корреляцию, используя как средства анализа, так и понятие функции.

Точечные диаграммы

Последующие действия описывают алгоритм построения и усовершенствования графика рассеяния при помощи Мастера диаграмм Excel.

1. Расположите данные в столбцах таблицы так, чтобы значения X (для горизонтальной оси) были слева, а У (для вертикальной оси) - справа, как показано на рис. 22. В данном примере не имеет большого значения, какую переменную принять за X, а какую – за Y.

2. Выделите значения X и Y (А2:В16), не включая метки над данными.

3. Щелкните мышью по кнопке Мастера диаграмм. или выберите в основном меню ВставкаôТочечная. Во всплывающем окне выберите Точечная с маркерами.

Рис.22. Исходная точечная диаграмма

4. Выберите в основном меню пункт Макет и введите с помощью соответствующих кнопок на панели инструментов название диаграммы «Яйценоскость кур»иназванияосей ("1-й признак" для названия оси значений X (горизонтальной оси) и "2-й признак" для оси значений Y (вертикальной оси).

5. Щелкните по кнопке Легенда и выберите Нет (Не добавлять легенду).

Диаграмма вложена в лист, как это показано на рис. 22. Данные об объектах демонстрируют общую определенную зависимость - в среднем у кур-дочерей сохраняется такая же закономерность по количеству снесенных яиц, что и у кур-матерей. Чем больше (меньше) снесено яиц за 10 дней отдельными курами в первой группе (матери), тем больше (меньше) яиц сносят за этот же период и их дочери.

ИНСТРУМЕНТ АНАЛИЗА: КОРРЕЛЯЦИЯ

Коэффициент корреляции - это полезная общая характеристика двумерных данных в том же смысле, в каком среднее значение и стандартное отклонение являются для одномерных данных полезными суммарными характеристиками. Коэффициент корреляции характеризует только линейную зависимость; в случае строго нелинейной зависимости (например, зависимость U-вида) коэффициент корреляции может быть близким к нулю. Полное название коэффициента корреляции звучит так: «Коэффициент корреляции смешанного произведения», что обычно сокращают до «корреляции».

Следующие шаги описывают вычисление коэффициента корреляции с помощью средств анализа данных.

1. Введите данные х и у в столбцы А и В, как показано на рис. 23, и введите Инструмент анализа: Корреляция в ячейку D1.

2. В меню Данные выберите Анализ данных. В диалоговом окне Анализа данных в списке Инструментов анализа выберите Корреляцию и нажмите ОК.

3. Укажите местоположение данных в строке ввода Входной интервал в части окна, относящейся к Входным данным, включая метки (А1:В11). Убедитесь, что данные сгруппированы По столбцам и отмечен пункт Метки в первой строке.

4. В части окна, относящейся к Параметрам вывода, выберите пункт Выходной интервал и укажите левую верхнюю ячейку области, в которую будут записаны результаты (D2).

⇐ Предыдущая 7 8 9 10 111213 14 15 16 Следующая ⇒