
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Затухающие колебания
4.3. Затухающие колебания
На систему, совершающую свободные затухающие колебания, действуют две обобщенные силы: возвращающая сила и сила трения:
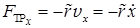 , (66)
, (66)
где 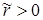 – обобщенный коэффициент сопротивления среды.
– обобщенный коэффициент сопротивления среды.
Закон затухающих колебаний имеет вид:
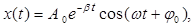 (67)
(67)
где 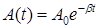 – экспоненциально убывающая амплитуда затухающих колебаний;
– экспоненциально убывающая амплитуда затухающих колебаний;
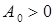 – начальная амплитуда (вещественная константа);
– начальная амплитуда (вещественная константа);
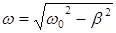 – частота затухающих колебаний;
– частота затухающих колебаний;
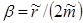 – коэффициент затухания для механического осциллятора,
– коэффициент затухания для механического осциллятора, 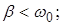
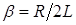 – коэффициент затухания для реального колебательного контура.
– коэффициент затухания для реального колебательного контура.
Логарифмический декремент затухания
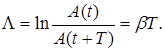 (68)
(68)
Средняя за период полная энергия затухающих колебаний
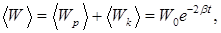 (69)
(69)
где 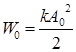 – начальное значение энергии.
– начальное значение энергии.
Добротность принято выражать также через отношение запасенной в системе энергии 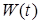 (69) к средней за период потере энергии
(69) к средней за период потере энергии 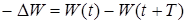 :
:
 . (70)
. (70)
При малом затухании добротность колебательной системы
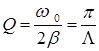 . (71)
. (71)
Задачи
103. (1) Через сколько колебаний амплитуда затухающих колебаний уменьшится в четыре раза, если период колебаний равен 2,1 с, а коэффициент затухания колебаний равен 0,043 с-1?
104. (1) Чему равен логарифмический декремент затухания колебаний математического маятника, если через пять колебаний их амплитуда уменьшается в два раза?
105. (1) Амплитуда затухающих колебаний математического маятника за 60 с уменьшилась вдвое. Во сколько раз она уменьшится за 180 с?
106. (2) Пружинный маятник массой 1,0 кг совершает колебания, при которых смещение груза от положения равновесия меняется с течением времени по закону: 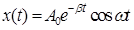 , где
, где 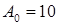 см;
см; 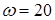 с-1;
с-1; 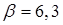 с-1. Найти: 1) ло-гарифмический декремент затухания; 2) во сколько раз изменится амплитуда колебаний после десяти полных колебаний; 3) собственную частоту колебаний маятника; 4) потенциальную энергию маятника спустя половину периода от начала колебаний.
с-1. Найти: 1) ло-гарифмический декремент затухания; 2) во сколько раз изменится амплитуда колебаний после десяти полных колебаний; 3) собственную частоту колебаний маятника; 4) потенциальную энергию маятника спустя половину периода от начала колебаний.
107. (1) За какое время амплитуда затухающих колебаний силы тока в реальном колебательном контуре уменьшится в два раза, если коэффициент затухания колебаний равен 0,75 с-1?
108. (1) Чему равен логарифмический декремент затухания колебаний в реальном колебательном контуре, если спустя 10 колебаний амплитуда колебаний силы тока уменьшается в три раза?
109. (2) В колебательном контуре, состоящем из катушки индуктивностью 20 мГн и конденсатора емкостью 10 нФ, за время, равное одному периоду, происходит убывание амплитуды энергии электрического поля в 1,2 раза. Найти сопротивление, логарифмический декремент затухания и добротность контура.
110. (3) В реальном колебательном контуре с емкостью 10 мкФ энергия элект-рического поля меняется по закону: 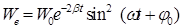 , где
, где 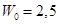 мкДж;
мкДж; 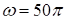 с-1;
с-1; 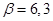 с-1. В начальный момент времени вся энергия сосредоточена в электрическом поле конденсатора. Найти: 1) активное сопротивление контура; 2) закон изменения заряда на обкладках конденсатора; 3) время, в течение которого амплитуда колебаний заряда уменьшится в два раза.
с-1. В начальный момент времени вся энергия сосредоточена в электрическом поле конденсатора. Найти: 1) активное сопротивление контура; 2) закон изменения заряда на обкладках конденсатора; 3) время, в течение которого амплитуда колебаний заряда уменьшится в два раза.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|