
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Сложение гармонических колебаний
4.2. Сложение гармонических колебаний
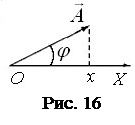 При сложении гармонических колебаний одного направления удобно использовать метод векторных диаграмм. Каждое колебание, например,
При сложении гармонических колебаний одного направления удобно использовать метод векторных диаграмм. Каждое колебание, например, 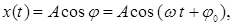 изображается вектором
изображается вектором 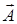 на плоскости (рис. 16). Длина вектора равна амплитуде колебания А. Угол между вектором
на плоскости (рис. 16). Длина вектора равна амплитуде колебания А. Угол между вектором 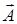 и горизонтальной осью равен фазе
и горизонтальной осью равен фазе 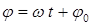 соответствующего колебания в данный момент времени.
соответствующего колебания в данный момент времени.
 При сложении двух гармонических колебаний одного направления и одинаковой частоты колебания представляются на диаг-рамме с помощью векторов
При сложении двух гармонических колебаний одного направления и одинаковой частоты колебания представляются на диаг-рамме с помощью векторов 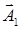 и
и 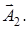
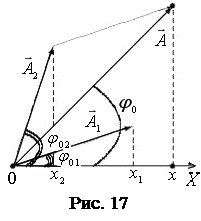
Вектор 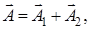 описывающий результирующее колебание, строится по правилам сложения векторов. На рис. 17 представлена векторная диаг-рамма, соответствующая сложению колебаний в начальный момент времени. Частота результирующего колебания
описывающий результирующее колебание, строится по правилам сложения векторов. На рис. 17 представлена векторная диаг-рамма, соответствующая сложению колебаний в начальный момент времени. Частота результирующего колебания  также равна w.
также равна w.
Амплитуда и начальная фаза результирующего колебания определяются соответственно по формулам:
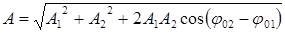 ; (63)
; (63)
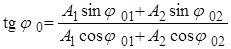 . (64)
. (64)
При сложении двух линейных взаимно перпендикулярных колебаний, совершаемых частицей в плоскости 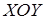 ,
,
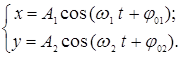 (65)
(65)
Уравнение результирующей траектории движения должно содержать только переменные 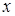 и
и 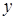 , но не должно содержать времени t. Такое уравнение получается, если каким-либо образом исключить из формул (65) время, например, выразить
, но не должно содержать времени t. Такое уравнение получается, если каким-либо образом исключить из формул (65) время, например, выразить 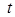 через
через 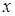 или y. Если частоты (периоды) относятся как целые числа (дробь
или y. Если частоты (периоды) относятся как целые числа (дробь 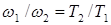 является рациональной), то траектория оказывается замкнутой, а движение периодическим.
является рациональной), то траектория оказывается замкнутой, а движение периодическим.
Задачи
101. (2) Для начального момента времени построить векторную диаграмму сложения двух гармонических колебаний одного направления и одинаковой частоты. Найти графически и аналитически амплитуду и начальную фазу результирующего колебания. Записать закон результирующего колебания. Законы складываемых колебаний имеют вид:
1) 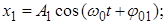
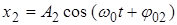 , где
, где 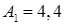 см;
см; 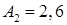 см;
см; 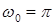 с-1;
с-1; 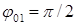 ;
; 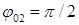 ;
;
2) 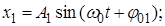
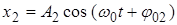 , где
, где 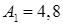 см;
см; 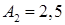 см;
см; 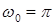 с-1;
с-1; 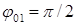 ;
; 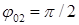 ;
;
3) 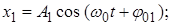
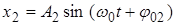 , где
, где 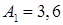 см;
см; 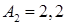 см;
см; 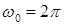 с-1;
с-1; 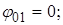
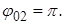
102. (2) Получить уравнение траектории частицы и построить траекторию в плоскости 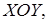 если частица одновременно участвует в двух взаимно перпендикулярных колебаниях:
если частица одновременно участвует в двух взаимно перпендикулярных колебаниях:
1) 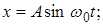
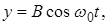 где
где 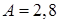 см;
см; 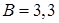 см;
см; 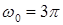 с-1;
с-1;
2) 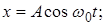
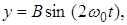 где
где 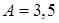 см;
см; 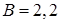 см;
см;  с-1;
с-1;
3) 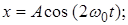
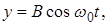 где
где 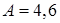 см;
см; 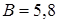 см;
см; 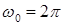 с-1.
с-1.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|