КОЛЕБАНИЯ. Гармонические колебания

4. КОЛЕБАНИЯ

4.1. Гармонические колебания

Колебания – это процесс, в котором какая-либо физическая величина пов-торяется с течением времени. Колебания, происходящие по закону косинуса или синуса, называются гармоническими.

Время одного полного колебания называется периодом Т.

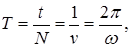(59)

где 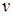– линейная частота колебаний (количество колебаний за единицу времени);

ω – циклическая (круговая) частота колебаний – количество колебаний за 2p с.

Дифференциальное уравнение гармонических колебаний имеет вид:

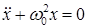, 60)

где х – обобщенная координата системы, т. е. смещение системы от положения равновесия, меняющееся со временем по гармоническому закону.

Решением такого дифференциального уравнения является функция:

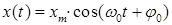(61)

или

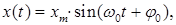(62)

где 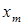= А – обобщенная амплитуда колебания, т. е. максимальное отклонение колеблющейся величины от положения равновесия;

ω₀ – циклическая (круговая) частота гармонических (собственных) колебаний;

j = 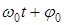- фаза колебания ( 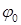- начальная фаза колебания).

Система, совершающая гармонические колебания, называется гармони-ческим осциллятором.

В табл. 1 приведены формулы, определяющие собственную частоту гармонических колебаний различных осцилляторов.

Таблица 1

Собственная частота гармонических колебаний различных осцилляторов

Гармонический осциллятор	Собственная частота
Пружинный маятник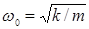
Физический маятник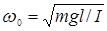
Математический маятник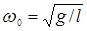
Идеальный колебательный контур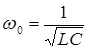

Между механическими и электромагнитными колебаниями много общего. В табл. 2 прослеживаются аналогии между основными характеристиками механических и электромагнитных колебаний.

Таблица 2

Соответствие основных характеристик

механических и электромагнитных колебаний

Колебания
механические	электромагнитные

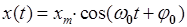
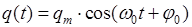
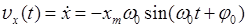
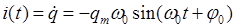
Окончание табл.2



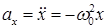
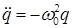
m	L
k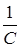

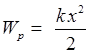
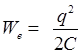
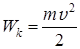
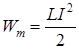
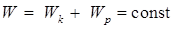
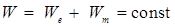
Задачи

91. (1) Найти собственную частоту колебаний математического маятника длиной 94 см и массой 0,43 кг.

92. (1) Период гармонических колебаний пружинного маятника равен 1,4 с. Масса груза 220 г. Найти коэффициент упругости пружины.

93. (2) Частица совершает гармонические колебания вдоль оси Х, при которых проекция ее скорости на эту ось меняется по закону: 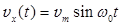, где 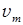= 2,5 см/с; 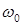= 2,4 с^-1. Найти амплитуду колебания, координату частицы и проекцию ее ускорения на ось 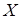в момент времени, равный четверти периода.

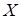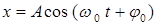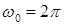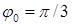94. (2) Пружинный маятник совершает гармонические колебания вдоль оси по закону: , где А = 5,2 см; с^-1; . Найти: 1) жесткость пружины маятника, если масса груза равна 1,2 кг; 2) момент времени, ближайший к началу колебаний, когда модуль ускорения маятника имеет максимальное значение; 3) полную энергию колебаний маятника.

95. (3) Стержень массой 1,5 кг и длиной 30 см укреплен так, что может вращаться относительно горизонтальной оси, проходящей через один из его концов. Его отклонили от положения равновесия на угол 10° и отпустили. Записать закон колебаний стержня. Найти: 1) период колебаний; 2) моменты времени, в которые кинетическая энергия стержня максимальна; 3) угловое ускорение маятника, его кинетическую и потенциальную энергию спустя одну треть периода колебаний.

96. (1) Колебательный контур состоит из конденсатора емкостью 5,1 мкФ и катушки индуктивностью 0,26 Гн. Определить максимальную силу тока i_m в контуре, если максимальная разность потенциалов на обкладках конденсатора 90 В. Сопротивлением контура пренебречь.

97. (1) В идеальном колебательном контуре сила тока в катушке меняется по закону: 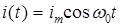, где 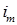= 2,5 А; 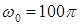с^-1. Емкость конденсатора 240 мФ. Найти законы изменения со временем заряда и напряжения на обкладках конденсатора.

98. (2) В идеальном колебательном контуре заряд на обкладках конденсатора меняется по закону: , где 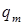= 1,4 мкКл; 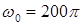с^-1. Индуктивность контура 0,48 мГн. Найти: 1) емкость контура; 2) начальную фазу колебаний, если в начальный момент времени заряд имел максимальное положительное значение; 3) силу тока в катушке в момент времени, равный 1/6 части периода колебаний; 4) законы изменения энергии электрического и магнитного полей со временем.

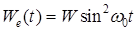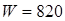99. (2) Энергия электрического поля в идеальном колебательном контуре меняется по закону: , где мкДж; 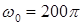с^-1. Найти: 1) индуктивность контура, если его емкость 20 пФ; 2) период собственных колебаний в контуре; 3) законы изменения заряда и силы тока со временем; 4) силу тока в момент времени, равный 1/4 периода колебаний.

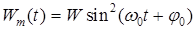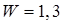100. (2) Энергия магнитного поля в идеальном колебательном контуре меняется по закону: , где мДж; 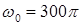с^-1. Индуктивность контура 0,23 мГн. Найти: 1) емкость контура; 2) период собст-венных колебаний в контуре; 3) начальную фазу колебаний, если в начальный момент времени заряд на обкладках конденсатора имел максимальное отрицательное значение; 4) законы изменения заряда и силы тока со временем.

⇐ Предыдущая 5 6 7 8 9 101112 13 14 Следующая ⇒