
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Метод определителей (метод Крамера).
2.Метод определителей (метод Крамера).
Найдем определитель системы 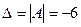 (см. п. 1). Так как
(см. п. 1). Так как  , то по теореме Крамера система имеет единственное решение.
, то по теореме Крамера система имеет единственное решение.
Вычислим определители матриц 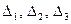 , полученных из матрицы
, полученных из матрицы 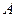 , заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:
, заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:
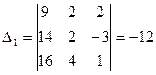 ,
, 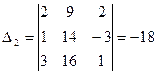 ,
,  .
.
Решение системы находим по формулам:
 ,
, 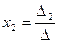 ,
,  ,
,
откуда получаем
 .
.
3.Метод Гаусса.
Замечание 1.1. Напомним, что метод Гаусса заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Преобразования Гаусса удобнее проводить не с самими уравнениями системы, а с матрицей их коэффициентов, то есть со строками расширенной матрицы системы.
К элементарным преобразованиям относятся:
1) перестановка местами двух строк матрицы;
2) умножение всех элементов строки на число, отличное от нуля;
3) прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на одно и то же число.
Расширенная матрица исходной системы имеет вид
 .
.
Для удобства преобразований, поменяем в расширенной матрице первую и вторую строки:
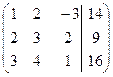 .
.
Далее умножаем первую строку на 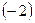 и прибавляем ко второй строке, потом умножаем первую строку на
и прибавляем ко второй строке, потом умножаем первую строку на 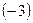 и прибавляем её к третьей строке. Третью строку полученной матрицы поделим на
и прибавляем её к третьей строке. Третью строку полученной матрицы поделим на 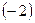 :
:

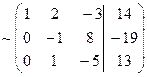
Вторую строку последней матрицы прибавляем к третьей, в результате получим
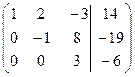 .
.
Запишем систему уравнений, соответствующую преобразованной матрице коэффициентов:
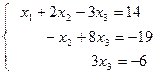 .
.
Из последнего уравнения находим 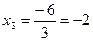 ; подставляем найденное значение
; подставляем найденное значение 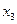 во второе уравнение системы:
во второе уравнение системы: 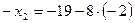 ,
, 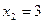 , и из первого уравнения:
, и из первого уравнения: 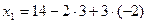 ,
,  .
.
Таким образом, решение системы: 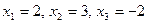 .
.
Задача 1. Решить систему линейных алгебраических уравнений: 1) методом обратной матрицы; 2) методом определителей; 3) методом Гаусса.
1.1.
| 1.2.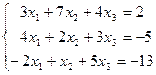
|
1.3.
| 1.4.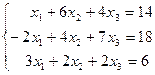
|
1.5.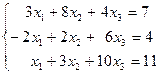
| 1.6.
|
1.7.
| 1.8. 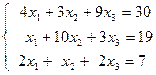
|
1.9.
| 1.10.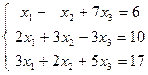
|
1.11.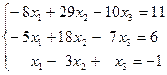
| 1.12.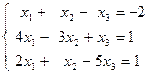
|
1.13.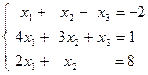
| 1.14.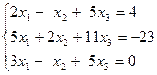
|
1.15.
| 1.16.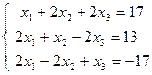
|
1.17.
| 1.18.
|
1.19.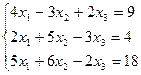
| 1.20.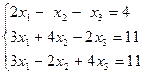
|
1.21.
| 1.22.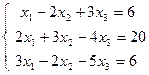
|
1.23.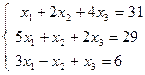
| 1.24.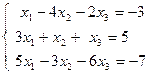
|
1.25.
| 1.26.
|
1.27.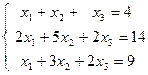
| 1.28.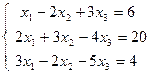
|
1.29.
| 1.30.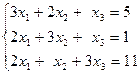
|
2. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|