Теорема Кронекера-Капелли

1.3. Теорема Кронекера-Капелли

Первым вопросом, возникающем при изучении системы (1.3) , является вопрос о ее совместности. Ответ на него дает теорема Кронекера-Капелли (без доказательства).

Теорема 1.1. Для совместности системы линейных алгебраических уравнений необходимо и достаточно, чтобы ранг матрицы А из коэффициентов при неизвестных был равен рангу расширенной матрицы , под которой пони-мают матрицу А, дополненную столбцом свободных членов:

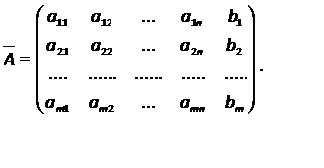
Приведем алгоритм решения системы из m уравнений с nнеизвестными:

Находим rangA и rang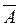. Если они равны, то система совместна , если не равны – система не имеет решений.
Если система совместна, выписываем равносильную систему, включа-ющую в себя только те уравнения, коэффициенты при неизвестных в которых образуют базисный минор.

Если система совместна и rangA=n, то систему можно решать по формулам Крамера или матричным способом. В этом случае система имеет единственное решение. Если rangA=r<n, то n-r членов, содержащих неизвестные с коэффициентами, не входящими в базисный минор, пе-реносим в правую часть. Эти неизвестные называются свободными пе-ременными и могут принимать любые значения. Неизвестные, остав-шиеся в левой части, называются главными (их rштук). Если rangA<n, то система имеет бесконечно много решений.
Решаем полученную систему r уравнений с r неизвестными по формулам Крамера или с помощью обратной матрицы.

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒