
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Анализ резистивных электрических цепей постоянного тока
2.4Анализ резистивных электрических цепей постоянного тока
2.4.1 Общие понятия
Методы анализа линейных электрических цепей основаны на законе Ома, законах Кирхгофа, на свойствах и теоремах линейных цепей. Наиболее общими являются метод контурных токов, метод узловых потенциалов и непосредственное применение законов Кирхгофа.
2.4.2 Законы Ома, Кирхгофа и закон сохранения энергии
Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка. Пусть имеется некоторый участок цепи (рис.1.3), крайние точки которого обозначены буквамиа и b.
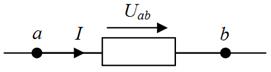
Рис. 1.3 Участок электрической цепи между точками а и b
Пусть ток I течет от точки а к точке b (от более высокого потенциала к более низкому). Следовательно, потенциал точкиа(φa) выше потенциала точки b(φb) на значение, равное произведению тока Iна сопротивление R:
| φa=φb+IR. |
В соответствии с определением напряжение между точкамиа и b
| Uab=φa-φb. |
Напряжение Uab=IRна сопротивлении равно произведению тока, протекающего по сопротивлению, на значение этого сопротивления.
В электротехнике разность потенциалов на концах сопротивления принято называть либо напряжением на сопротивлении, либо падением напряжения.Положительное направление падения напряжения на каком-либо участке (направление отсчета этого напряжения), указываемое на рисунках стрелкой, совпадает с положительным направлением отсчета тока, протекающего по данному сопротивлению.
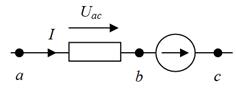
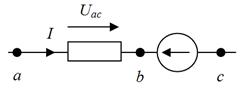
Рассмотрим вопрос о напряжении на участке цепи, содержащей кроме сопротивления R, ЭДС Е (рис. 1.4, а, б). Найдем разность потенциалов (напряжение) между точкамиа и с для этих участков. По определению Uaс=φa-φс. Выразим потенциал точкиа через потенциал точки с. При перемещении от точки с к точке b встречно направлению ЭДС Е (см. рис. 1.4, а) потенциал точки b оказывается меньше, чем потенциал точки с, на значение ЭДС Е:φb=φc-E. При перемещении от точки с к точке b согласно направлению ЭДС Е (рис.1.4, б) потенциал точки b больше, чем потенциал точки с,на значение ЭДС: φb=φc+E.
Так как ток течет от более высокого потенциала к более низкому, то в обеих схемах потенциал точкиа выше потенциала точки b на величину падения напряжения на сопротивлении R:φа=φb+IR.
| 
|
| а) | б) |
| Рис. 1.4. Участок цепи, содержащий R, ЭДС Е:потенциал точки b меньше, чем потенциал точки с, на значение ЭДС (а); потенциал точки b больше, чем потенциал точки с, на значение ЭДС (б) | |
Таким образом, для рис. 1.4, а:
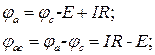
| (1.9) |
для рис. 1.4, б:
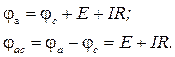
| (1.10) |
Положительное направление напряжения Uaспоказывают стрелкой ота к с. Согласно определению, Uса=φс-φа, поэтому Uас=-Uса, т.е. изменение чередования индексов равносильно изменению знака этого напряжения. Следовательно, напряжение может быть как положительной величиной, так и отрицательной.
Закон Ома для участка цепи, не содержащего ЭДС Е, устанавливает связь между током и напряжением на этом участке. Применительно к рис.1.4
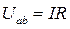 или или 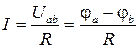 . .
| (1.11) |
Закон Ома для участка цепи, содержащего источник ЭДС Е, позволяет найти ток этого участка по известной разности потенциалов (φa-φс) на концах этого участка цепи и имеющейся на участке ЭДС Е.
Так, из уравнения (1.11) для схемы рис.1.4, а следует
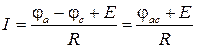
|
Из уравнения (1.11) для схемы рис.1.4, б следует:
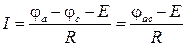
|
В общем случае
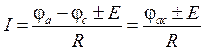 . .
| (1.12) |
Все электрические цепи подчиняются первому и второму законам Кирхгофа.
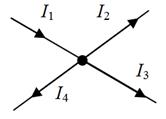
Первый закон Кирхгофа можно сформулировать двояко (рис.1.5, а):
1) алгебраическая сумма токов, подтекающих к какому-либо узлу схемы, равна нулю;
2) сумма подтекающих клюбому узлу токов равна сумме утекающихот этого узла токов.
| 
|
| а) | б) |
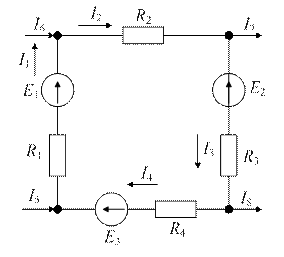
| Рис. 1.5. К пояснению первого (а) и второго (б) законов Кирхгофа | |
Применительно к (рис.1.5, а), если подтекающие токи к узлу считать положительными, а вытекающие - отрицательными, то согласно первой формулировке I1-I2-I3-I4=0; согласно второй I1=I2+I3+I4. Физически первый закон Кирхгофа означает, что движение электрических зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются. В противном случае изменялись бы потенциалы узлов и токи в ветвях.
Второй закон Кирхгофа также можно сформулироватьдвояко (рис.1.5, б):
1) алгебраическая сумма падений напряжений в любом замкнутом контуре равна алгебраической сумме ЭДС, входящих в данный контур:
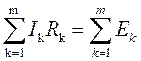 . .
| (1.13) |
где m - число резистивных элементов; п – число ЭДС в контуре (в каждую из сумм соответствующие слагаемые входят со знаком плюс, если они совпадают с направлением обхода контура, и со знаком минус, если они не совпадают с ним);
| SEk = SIiRi, E1-E2+E3 = I1R1+ I2R2+ I3R3+ I4R4. | (1.14) |
Правило: если направление тока и Е совпадает с направлением обхода то в уравнении берётся со знаком «+», если не совпадает, то «-».
2) алгебраическая сумма напряжений вдоль любого замкнутого контура (рис.1.5, б)
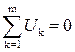 , ,
| (1.15) |
где т - число элементов контура.
Законы Кирхгофа справедливы длялинейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|