Основные понятия. Решение систем линейных уравнений с помощью обратной матрицы и по формулам Крамера

1.1. Основные понятия

Рассмотрим систему m линейных уравнений с n неизвестными :

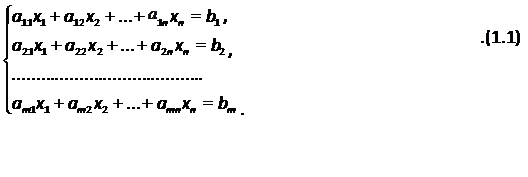
Обозначим матрицу из коэффициентов А, матрицу – столбец из свободных членов В, матрицу – столбец из неизвестных Х. Используя понятие произве-дения матриц, систему (2.1) можно кратко записать в матричной форме:

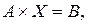(1.2)

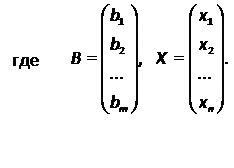
Определение 1. Упорядоченный набор n чисел 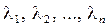называется решением системы (2.1), если в результате замены неизвестных 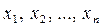числами 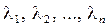все уравнения системы превратятся в верные число-вые равенства.

Определение 2. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Определение 3. Система (2.1) называется однородной, если .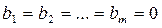

Очевидно, что однородная система всегда имеет тривиальное решение .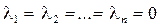

1.2. Решение систем линейных уравнений с помощью обратной матрицы и по формулам Крамера

Рассмотрим систему

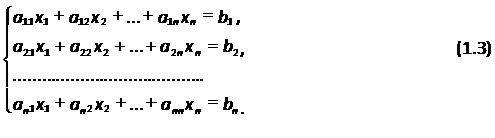
В матричной форме система имеет вид 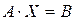. Пусть 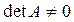, сле-

довательно, существует обратная матрица 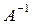. Умножим левую и правую части 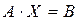на 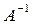с левой стороны: 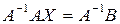. Так как 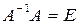и 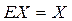, то решение (2.3) в матричной форме имеет вид

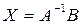. (1.4)

Для вывода формул Крамера ограничимся случаем n=3. Матричное равенство запишется в виде

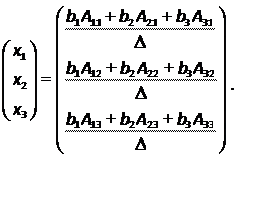
Выражение 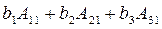- разложение по первому столбцу определителя

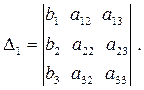
Аналогично

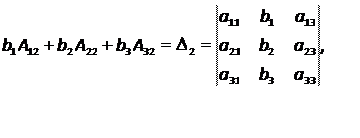
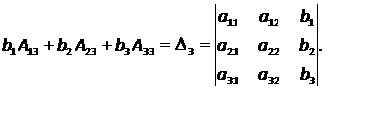
Следовательно, систему из n уравнений с n неизвестными с определителем из коэффициентов при неизвестных, отличным от нуля, можно решать по формулам, которые называются формулами Крамера:

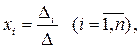(1.5)

где ∆ - определитель из коэффициентов при неизвестных, 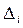- определитель, полученный из ∆ заменой i-го столбца на столбец из свободных членов.

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒