Чистый изгиб с растяжением (сжатием)

11.3. Чистый изгиб с растяжением (сжатием)

Эту деформацию представим себе как сочетание косого изгиба и чистого сжатия, при котором напряжения суммируются алгебраически:

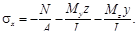
Тождественную схему деформирования наблюдаем в случае приложения продольной нагрузки F со смещением (эксцентриситетом) относительно центра тяжести поперечного сечения, в точке (z_F, y_F) (рис.11.2, а). Этот случай получил название внецентренного сжатия¹.

Применив метод сечений, обнаружим в любом поперечном сечении продольную силу N= – F и изгибающие моменты: М_у= Fz_F и M_z= Fy_F. Таким образом, напряжения можно представить в другом виде:

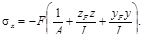
После введения радиусов инерции формула принимает вид

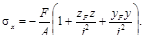
Так как в точках нейтральной оси сечения σ_x = 0, то уравнение этой оси будет

Рис. 11.2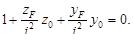

¹Все выводы, относящиеся к внецентренному сжатию бруса, могут быть применены и к случаю внецентреннего растяжения при замене сжимающей силы -F на +F.

После подстановки в уравнение этой прямой линии последовательно значений координат точки на оси у: z₀= 0 и у₀= a_у и на оси z: у₀= 0 и z₀= a_z получаем отрезки:

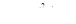
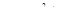
Минусы указывают на то, что нулевая линия и точка приложения силы F (полюс) располагаются по разные стороны от центра тяжести (рис.8.13,б).

Докажем следующую теорему: при перемещении полюса по прямой нулевая линия вращается около неподвижной точки.

Пусть f – f есть прямая, отсекающая отрезки b_у и b_z на осях координат (рис.11.3). Примем ее за нулевую линию, тогда координаты соответствующего полюса – точки Q суть

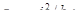
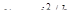
Если, наоборот, силу приложить в точке на линии f – f, то согласно упомянутой выше теореме, напряжение в точке Q окажется равным ну-

лю. Совокупность нулевых линий для всех положений полюса на линии f – f есть пучок прямых, проходящих через точку Q.

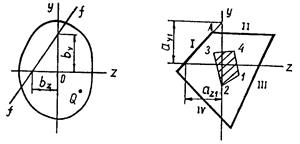
Рис. 11.3 Рис.11.4

В частном случае, когда полюс движется по прямой, проходящей через центр тяжести, нулевая линия перемещается параллельно себе, ибо пропорциональное изменение координат у_F и z_F влечет также пропорциональное изменение отрезков а_y и а_z.

При у_F → 0 и z_F → 0 нулевая линия уходит в бесконечность, что соответствует наступлению чистого растяжения (сжатия). При у_F → ∞ и z_F → ∞ а_y → 0 и а_z → 0, что соответствует наступлению чистого косого изгиба.

В окрестности центра тяжести существует область, называемая ядром сечения. Если след силы F (или равнодействующей нескольких сил) находится внутри этой области, то нейтральная линия проходит за пределами сечения, и, следовательно, во всех его точках напряжения будут одного знака.

Покажем построение контура ядра сечения. Пусть нулевая линия совпадает со стороной I контура сечения, отсекая на осях у и z отрезки а_y₁ и а_z₁ (рис.11.4).

Тогда координаты точки 1 на контуре ядра сечения:

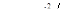
При совпадении нулевой линии с гранью II таким же способом находим координаты точки 2 (z_F₂ и у_F₂) на контуре ядра сечения. При вращении нулевой линии вокруг вершины А соответствующая ей точка приложения силы F перемещается вдоль отрезка 1–2. Контур ядра сечения будет многоугольником, число сторон которого равно числу сторон сечения бруса.

Читателю предлагается установить, что для прямоугольного сечения с размерами b и h ядро сечения имеет форму ромба с диагоналями, равными b/3 и h/3, а для круга радиусом r − концентрический круг радиусом r/4.

Зная контур ядра сечения, можно определить, будут ли напряжения при заданном положении силы F иметь одинаковые или разные знаки в пределах поперечного сечения бруса. Это важно знать для материалов, не обладающих одинаковой прочностью на растяжение и сжатие. Такими являются бетон, чугун, кирпичная кладка и др.

⇐ Предыдущая 42 43 44 45 464748 49 50 51 Следующая ⇒