СЛОЖНОЕ СОПРОТИВЛЕНИЕ. Общие понятия. Чистый косой изгиб призматического бруса

11. СЛОЖНОЕ СОПРОТИВЛЕНИЕ

11.1. Общие понятия

Если в поперечном сечении бруса возникают два или более внутренних силовых фактора, учитывать которые обязательно необходимо в расчетах на прочность, то говорят о сложном сопротивлении.

Хотя при прямом поперечном изгибе в сечении возникают и М_z и Q_у, но в подавляющем большинстве случаев расчеты на прочность и жесткость ведут без учета влияния поперечных сил, то этот случай считают простым соп-ротивлением.

Если в поперечном сечении в опасной точке бруса напряженное состояние является линейным (одноосным), хотя и вызывается несколькими внутренними усилиями, то оценку прочности проводят по условию:

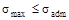
т.е. использовать теории прочности просто не нужно. Это характерно для косого изгиба, внецентренного растяжения и сжатия.

Если в опасной точке бруса возникает плоское напряженное состояние, то оценить прочность можно только по одной из теорий прочности, выбор которой определяется предельным состоянием данного материала в данных конкретных условиях нагружения (температура, скорость нагружения и т.п.). Такие расчеты проводят при изгибе с кручением, сжатии с изгибом и кручени-ем.

11.2. Чистый косой изгиб призматического бруса

В отличие от прямого изгиба общий случай изгиба, при котором плоскость действия момента не содержит главную ось инерции сечения, называется косым изгибом.

Косой изгиб удобнее всего рассматривать как одновременный изгиб бруса моментами M_z и М_у, для которых оси z и у являются главными центральными осями инерции сечения, а плоскости действия xz и xу –главными плоскостя-ми бруса.

Рис.11.1 Зададим моменты M на торцах бру-са в силовой плоскости, составляющей с главной плоскостью ху угол β, показанный на рис.11.1, а как отклонение от оси у силовой линии f – f – следа силовой плоскости на плоскости сечения бруса. Тогда М_z= Mcosβ , M_у= Msinβ (на рис.11.1, б)моментные векторы отложены на нормалях к плоскостям

действия моментов). Напряжение в точке (у,z) можно определить как алгебраическую сумму напряжения от M_z и M_y :

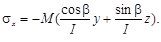
Как и при прямом изгибе, напряжения распределяются по закону плоскости.

Так как в точках нейтральной оси сечения σ_х= 0, то уравнение этой оси будет

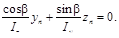
Другими словами, нейтральной осью при косом изгибе является прямая, проходящая через начало координат (центр тяжести сечения) и составляющая с осью z угол φ, определяемый из уравнения

tg tgβ

Минус показывает, что нейтральная ось и силовая линия лежат в двух смежных четвертях. При I_z ≠ I_y угол φ не равен углу β, т.е. нейтральная ось не перпендикулярна силовой плоскости, как это имело место при прямом изгибе.

К случаю, когда I_z = I_y и все центральные оси сечения являются главными, понятие "косой изгиб" неприменимо (φ = β ).

Определить примерное положение нейтральной оси можно, сопоставив знаки напряжений от моментов M_z и М_у в четвертях. Нейтральная ось пройдет через те четверти, где эти напряжения вычитаются.

Линия равных напряжений в сечении

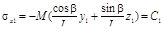
имеет тот же угловой коэффициент, что и нейтральная ось, т.е. параллельна ей. Это предопределяет характер эпюры σ_х (см. рис.11. 1,а). Поскольку напряжения σ_х распределяются по закону плоскости, проходящей через нейтральную ось, они будут наибольшими для точек, наиболее удаленных от этой оси.

Полный прогиб равен геометрической сумме перемещений w и v вдоль главных осей z и у:

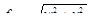
Направление прогиба определим функцией

tgα = v/w.

Величины v и w пропорциональны соответственно

M_z/I_z = (M cosβ)/I_z и M_y/I_y = (M sinβ)/I_y.

Следовательно,

tgα = (I_y /I_z) ctgβ = k₁.

В то же время угловой коэффициент нейтральной оси

tgφ = – (I_z/I_y) tgβ = k₂.

Так как k₂= –1/k₁, то направление полного прогиба перпендикулярно нейтральной оси. Следовательно, плоскость изгиба нормальна к нейтральному слою.

⇐ Предыдущая 41 42 43 44 454647 48 49 50 Следующая ⇒