
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Расчёт безмоментных оболочек вращения
11.5. Расчёт безмоментных оболочек вращения
В технике широко применяются элементы конструкций, которые с точки зрения расчета на прочность и жесткость могут быть отнесены к тонким оболо-чкам. Принято считать оболочку тонкой, если отношение ее толщины к габа-ритному размеру меньше 1/20. Для тонких оболочек применима гипотеза пря-мых нормалей: отрезки нормали к срединной поверхности остаются прямыми и нерастяжимыми после деформирования. В этом случае имеет место линейное распределение деформаций, а следовательно и нормальных напряжений (при малых упругих деформациях) по толщине оболочки.
Поверхность оболочки получают вращением плоской кривой вокруг оси, лежащей в плоскости кривой. Если кривую заменить прямой линией, то при вращении ее параллельно оси получается круговая цилиндрическая оболочка, а при вращении под углом к оси - коническая.
В расчетных схемах оболочку представляют ее срединной поверхностью (равноудаленной от лицевых). Срединную поверхность обычно связывают с криволинейной ортогональной системой координаты Ө и φ. Углом θ ( 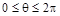 ) определяется положение параллели линии пересечения середин-ной поверхности с плоскостью, проходящей нормально к оси вращения.
) определяется положение параллели линии пересечения середин-ной поверхности с плоскостью, проходящей нормально к оси вращения.


Рис.11.6 Рис. 11.7
Через нормаль с серединой поверхности можно провести множество пло-скостей, которые будут нормальны к ней и в сечениях с ней образовывать ли-нии с разными радиусами кривизны. Два из этих радиусов имеют экстремаль-ное значения. Линии, которым они соответствуют, называются линиями главных кривизн. Одна из линий является медианой, её радиус кривизны обозначим r1. Радиус кривизны второй кривой – r2 (центр кривизны лежит на оси вращения). Центры радиусов r1 и r2 могут совпадать (сферическая оболоч-ка), лежать по одну или по разные стороны срединной поверхности, один из центров может уходить в бесконечность (цилиндрическая и коническая оболоч-ки).
При составлении основных уравнений усилия и перемещения относим к нормальным сечениям оболочки в плоскостях главных кривизн. Составим ура-внения для внутренних усилий. Рассмотрим бесконечно малый элемент оболо-чки (рис. 11.6), вырезанный двумя смежными меридиональными плоскостями (с углами θ и θ+dθ) и двумя смежными параллельными кругами, нормальными к оси вращения (с углами φ и φ+dφ). В качестве системы осей проекций и моментов избираем прямоугольную систему осей x, y, z. Ось y направлена по касательной к медиану, ось z – по нормали.
В силу осевой симметрии (нагрузка P=0) на элемент будут действовать только нормальные усилия. Nφ - погонное меридиональное усилие, направлен-ное по касательной к меридиану: Nθ - погонное кольцевое усилие, направлен-ное по касательной к окружности. Уравнение ΣХ=0 обращается в тождество. Спроектируем все силы на ось z:
2Nθr1dφ 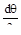 sinφ+[
sinφ+[ 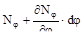 ]rodθdφ+Pzr1dφrodθ=0.
]rodθdφ+Pzr1dφrodθ=0.
Если пренебречь бесконечно малой величиной высшего порядка ( 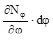 )ro dθ dφ и разделить уравнение на r1 ro dφ dθ, то принимая во внима-ние, что
)ro dθ dφ и разделить уравнение на r1 ro dφ dθ, то принимая во внима-ние, что 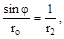 получим уравнение, принадлежащее П. Лапласу:
получим уравнение, принадлежащее П. Лапласу:
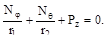
Вместо уравнения ΣY=0 для рассматриваемого элемента составим урав-нение равновесия верхней части оболочки (рис. 11.6). Спроектируем все силы на ось вращения:
Nφ 
uде: Rv- вертикальная проекция равнодействующей внешних сил, приложенных к отрезанной части оболочки. Итак,
Nφ= 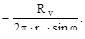
Подставив значения Nφ в уравнение Лапласа, найдём Nθ. Определение усилий в оболочке вращения по безмоментной теории представляет собой статически определимую задачу. Это стало возможным в результате того, что мы сразу постулировали закон изменения напряжений по толщине оболочки – считали их постоянными.
В случае сферического купола имеем r1= r2= r и rо= r 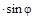 . Если нагрузка задана в виде интенсивности P на горизонтальную проекцию оболочки, то
. Если нагрузка задана в виде интенсивности P на горизонтальную проекцию оболочки, то
Rv= 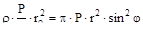 , и
, и
Nφ= 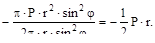
Таким образом, в меридиональном направлении купол равномерно сжат. Составляющие поверхностной нагрузки вдоль нормали z равна Pz=P 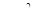 . Подставляем значения Nφ и Pz в уравнение Лапласа и находим из него:
. Подставляем значения Nφ и Pz в уравнение Лапласа и находим из него:
Nθ= 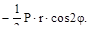
Кольцевые сжимающие усилия достигают максимума в вершине купола при φ = 0. При φ = 45º - Nθ=0; при φ > 45  - Nθ=0 становится растягивающим и достигает максимума при φ = 90
- Nθ=0 становится растягивающим и достигает максимума при φ = 90  .
.
Горизонтальная составляющая меридионального усилия равна:
H=Nφ 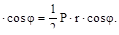
Рассмотрим пример расчёта безмоментной оболочки. Магистральный трубопровод заполнен газом, давление которого равно Р.
Здесь r1=R, r2= 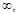 а в соответствии с ранее принятым допущением, что напряжения распределяются равномерно по толще δ оболочки
а в соответствии с ранее принятым допущением, что напряжения распределяются равномерно по толще δ оболочки
Nφ 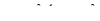 и Nθ=
и Nθ= 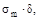
где: σm- нормальные меридиональные напряжения, а
σt- окружные (широтные, кольцевые) нормальные напряжения.
σt 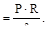
11.6 Практикум
Примеры - рассмотрены в разделе V
Вопросы для повторения
1. В каком случае изгиб называют косым?
2. Применимо ли определение “косой изгиб” для балки круглого поперечного сечения? Обоснуйте.
3. Как определяется положение нейтральной оси при косом изгибе?
4. Проходит ли нейтральная ось при косом изгибе через центр тяжести сече-ния? Обоснуйте.
5. Какие точки сечения будут опасными при косом изгибе?
6. Как определяют перемещения при косом изгибе?
7. Какие напряжения возникают в точках поперечного сечения при внецентрен-ном растяжении?
8. Проходит ли нейтральная ось при внецентренном растяжении через центр тяжести сечения? Обоснуйте.
9. Чему равно нормальное напряжение в центре тяжести сечения при внецен-тренном растяжении?
10. Могут ли при внецентренном растяжении возникать сжимающие напряже-ния в точках поперечного сечения?
11. Что называют ядром сечения?
12. Какими будут напряжения во всех точках сечения если известно, что след растягивающей силы находиться внутри ядра сечения?
13. Какие напряжения возникают в поперечном сечении бруса при изгибе с кручением?
14. Как находят опасные сечения бруса круглого сечения при изгибе с кручени-ем?
15. Какие точки круглого бруса являются опасными и какое напряженное сос-тояние в этих точках при кручении с изгибом?
16. Как выполняют проверку безопасной прочности при кручении с изгибом круглого бруса?
17. Какие допущения вводят при расчёте оболочек вращения по безмоментной теории?
18. Как определить меридиональные и окружные (широтные) нормальные нап-ряженния при расчёте тонкостенной оболочки вращения?
Тесты для повторения
В опасном поперечном сечении бруса из пластичного материала действуют Mz, My, N в напряжениях, указанных на рисунке. Какая точка будет опасной?
(а) 1; (б) 2; (в) 3; (г) 4.
 Ответ: (в), поскольку составляющие напряжения в точке 3 от каждого из изображённых внутренних факторов вызывают растягивающие напряжения.
Ответ: (в), поскольку составляющие напряжения в точке 3 от каждого из изображённых внутренних факторов вызывают растягивающие напряжения.
 2. Если на консольную балку, имеющую круглое поперечное сечение диамет-ром D действуют две взаимно перпендикулярные силы в плоскости поперечно-го сечения, а предел текучести σу извес-тен, то фактический коэффициент запа-са прочности n будет равен:
2. Если на консольную балку, имеющую круглое поперечное сечение диамет-ром D действуют две взаимно перпендикулярные силы в плоскости поперечно-го сечения, а предел текучести σу извес-тен, то фактический коэффициент запа-са прочности n будет равен:
(а) 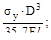 (б)
(б) 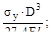
(в) 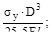 (г)
(г) 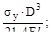
Ответ: (б). Опасным сечением будет сечение в заделке, где Mz мах=2.5Fl и Mу мах=Fl.
Приведённый изгибающий момент Mtot= 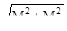 в опасном сечении равен
в опасном сечении равен 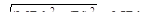
Действующие в опасной точке опасного сечения:
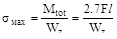
Коэффициент запаса прочности
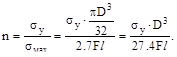
 3. Короткий стержень, имеющий прямоугольное сечение с размерами h > b, сжат силой F, приложенной в первом случае в точке А, а во втором – в точке В. Какой случай опаснее? Ответ дать сравнив возникающие нормальные напряжения
3. Короткий стержень, имеющий прямоугольное сечение с размерами h > b, сжат силой F, приложенной в первом случае в точке А, а во втором – в точке В. Какой случай опаснее? Ответ дать сравнив возникающие нормальные напряжения 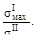 Это отношение равно:
Это отношение равно:
(а) 2.0; (б) 1.5;
(в) 1.0; (г) 0.5.
Ответ: (в), поскольку в первом случае максимальная величина
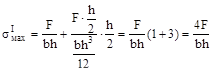 (опасные точки на линии, где приложена сила F), а во втором случае
(опасные точки на линии, где приложена сила F), а во втором случае 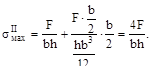
 4. Сила F действует в плоскости торцевого сечения балки. Во сколько раз воз-растут наибольшие напряжения σмах, если направление силы F отклониться от вертикального на угол α =30º? Попе-речное сечение – двутавр № 24 (Wz=298см4; Wy=34.5см4).
4. Сила F действует в плоскости торцевого сечения балки. Во сколько раз воз-растут наибольшие напряжения σмах, если направление силы F отклониться от вертикального на угол α =30º? Попе-речное сечение – двутавр № 24 (Wz=298см4; Wy=34.5см4).
(а) 2; (б) 3; (в) 4; (г) 5.
Ответ: (г), поскольку при вертикаль-ном приложении (чистый изгиб) 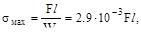 а при отклоне-
а при отклоне-
нии
силы F на 30 º (косой изгиб) 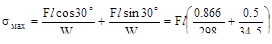 = =17.4·10-3 Fl, более чем в пять раз превышает первый случай.
= =17.4·10-3 Fl, более чем в пять раз превышает первый случай.
 5. Если в поперечном сечении стержня действуют два внутренних силовых фактора Mz и My, а наибольшие напряжения от каждого из них в отдельности известны (σмах(Mz) =150МПа; σмах(Mу) =80МПа), то большее суммарное напряжение равно:
5. Если в поперечном сечении стержня действуют два внутренних силовых фактора Mz и My, а наибольшие напряжения от каждого из них в отдельности известны (σмах(Mz) =150МПа; σмах(Mу) =80МПа), то большее суммарное напряжение равно:
(а) 170; (б) 190; (в) 210; (г) 230.
Ответ: (а), поскольку изгибающие моменты действу-ют во взаимно перпендикулярных плоскостях, то
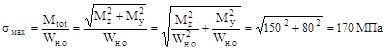 .
.
6. Если стержень из стали Ст.3 прямоугольного поперечного сечения находить-ся под действием двух сил F1 и F2, то опасной в заделке является точка:
 (а) 1; (б) 2; (в) 3; (г) 4;
(а) 1; (б) 2; (в) 3; (г) 4;
Ответ: (в) поскольку в этой точке все три внутренние силовые факторы вызывают одновременно сжатие, а материал пластич-ный.
Контрольные тесты
1. Стержень загружен двумя одинаковыми силами. Как изменится максималь-ное напряжение, если одну из сил убрать?
 (а) не изменится;
(а) не изменится;
(б) уменьшится в 2 раза;
(в) возрастёт в 1.5 раза;
(г) возрастёт в 2.5 раза.
2. Как изменится напряжение в точке А, если точку приложения силы перенести из точки А в точку В?

(а) возрастёт; (б) уменьшится;
(в) не измениться; (г) обратиться в ноль.
 3. Максимальное напряжение в стержне равно:
3. Максимальное напряжение в стержне равно:
(а) 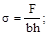 (б)
(б) 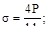
(в) 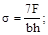 (г)
(г) 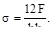
4. Допускаемое напряжение σadm. Чему равно максимальное значение силы F?

(а) 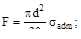 (б)
(б) 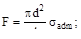
(в) 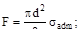 (г)
(г) 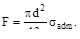
5. Как измениться максимальное напряжение в стержне, если точку прилроже-ния силы перенести в точку В?

(а) уменьшится; (б) не изменится;
(в) возрастёт; (г) станет равным 0.
6. Как изменится напряжение в точке А, если точку приложения силы перенес-ти из точки А в точку В?

(а) уменьшится; (б) не изменится;
(в) возрастёт; (г) станет равным 0.
7. Как изменится напряжение в точке А (см. рис. задачи 6), если силу перенес-ти в центр тяжести сечения?
(а) уменьшится; (б) не изменится; (в) возрастёт; (г) станет равным 0.
8. Как изменится напряжение в центре тяжести сечения стержня (точка О), если точку приложения силы (см. рис. к задаче 6) перенести из точки А в точку В?
(а) уменьшится; (б) не изменится; (в) возрастёт; (г) станет равным 0.
9. Укажите правильное положение нейтральной линии, если сила приложена параллельно оси стержня в точке А.

(а) 1-1; (б) 2-2;
(в) 3-3; (г) 4-4.
 10. На первом этапе действуют две равные силы F, параллельные оси стержня. Если на втором этапе убрать одну из сил, то максимальное напряжение σadm:
10. На первом этапе действуют две равные силы F, параллельные оси стержня. Если на втором этапе убрать одну из сил, то максимальное напряжение σadm:
(а) уменьшится на 50%;
(б) возрастёт на 50%;
(в) возрастёт на 150%;
(г) возрастёт на 250%.
11. Если к стержню приложены две силы- F и 2F, то наибольшее напряжения σмах будет равно:

(а) 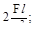 (б)
(б) 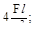
(в) 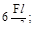 (г)
(г) 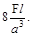

12. Вдоль оси стержня круглого поперечного сечения с квадратным отверстием в точке К (произвольной на внешнем контуре) приложена сила F=1000кН. Макси-мальное напряжение в МПа равно по модулю:
(а) 140; (б) 155;
(в) 170; (г) 185.
13. Если внецентренно приложенная сила F сжимает стержень из хрупкого материала 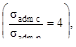 то допускаемое значение силы
то допускаемое значение силы
 F равно:
F равно:
(а) 0.14b·h·σadm p; (б) 0.17b·h·σadm p;
(в) 0.2 b·h·σadm p; (г) 0.25 b·h·σadm p.
 14. Укажите правильную эпюру σ.
14. Укажите правильную эпюру σ.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|