
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
РАЗДЕЛ III. СТЕРЖНЕВЫЕ СИСТЕМЫ
РАЗДЕЛ III. СТЕРЖНЕВЫЕ СИСТЕМЫ
12. Расчёт статически неопределимых систем методом сил
12.1 Основная система и сущность метода
Статически неопределимыми называют системы, в которых невозможно определить все реакции в связях закрепления, а также внутренние усилия в эле-ментах системы из уравнений статического равновесия. Но термин “лишние связи” является условным, поскольку при их отсутствии прочность и жёст-кость системы значительно снижается. Этот термин означает, что связи лишние только в плане превышения их количества числа независимых уравнений ра-вновесия.
Степень статической неопределимости можно определить как разность между числом искомых усилий и числом независимых уравнений равновесия, которые можно составить для рассматриваемой системы.
Для плоской системы положение жёсткого тела характеризуется тремя независимыми параметрами – двумя координатами и углом поворота, следова-тельно для равновесия на плоскости достаточно наложение трёх внешних свя-зей, что соответствует и трём независимым уравнениям равновесия. Если плос-кая система состоит из Д жёстких тел (дисков), то количество параметров, оп-ределяющих положение этой системы будет равно ЗД. Если они соединены ша-рнирами, то каждый шарнир, соединяющий две части системы, разрешая взаимный поворот, устраняет возможность взаимного смещения, т.е. уменьша-ет количество возможных перемещений системы, накладывая две дополнитель-ные связи. Каждый из опорных стержней устраняет возможность перемещения системы в соответствующем направлении. Тогда степень статической неопре-делимости, определяемую внешними связями можно подсчитать по формуле:
К=ЗД-2Ш-С,
где: Д- число частей системы, каждая из которых может рассматриваться как абсолютно жёсткое тело.
Ш- количество простых шарниров в системе, соединяющих два “диска”.
С- число опорных стержней.
Если К=0, то имеем статически определимую систему, если К<0 – статически неопределимую.
Для расчёта статически неопределимой системы дополнительно к урав-нениям статики необходимо составить К уравнений совместности перемещения в точках системы.
Для заданной системы (рис. 12.1 а)
К= 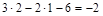
Следовательно система дважды статически неопределима, имеются две лиш-них связи. Если у заданной системы отбросить две “лишних” связи то образуем основную систему. Основная система статически определима, но при её обра-зовании необходимо обеспечить, что бы она не превратилась в механизм. Эта система может быть эквивалентна исходной, если к ней будут приложены в на-правлении отброшенных связей усилия Х1 и Х2 (рис. 12.1, б) значения которых следует определить из ограничений (совместности перемещений), которые на-кладывали отброшенные связи: 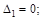
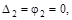 т.е. перемещения в гори-
т.е. перемещения в гори-
 зонтальном направлении правой опорной точки и угол поворота опорного сече-ния правой стойки равны нулю.
зонтальном направлении правой опорной точки и угол поворота опорного сече-ния правой стойки равны нулю.
Эти усилия рассматрива-ются как основные и дают назва-ние метода расчёта- метод сил. Определив усилия в “лишних связях”, задача оказывается ста-тически определимой. Для опре-деления перемещений следует воспользоваться универсальным методом-методом Мора, полу-чившего название по имени не-меецкого учёного, предложившего его. Рис. 12.1
12.2.Определение перемещений методом Мора
При использовании этого метода (в литературе его называют: методом возможной работы; методом фиктивной нагрузки; методом единичной нагруз-ки) необходимо рассматривать две системы нагрузок, действующих на кон-струкцию. Первая система включает все реальные нагрузки, а вторая система включает только единичную нагрузку, которая действует на конструкцию. Еди-ничная нагрузка представляет собой фиктивную или искусственно введённую нагрузку, которая позволяет определить перемещение 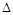 конструкции при действии реальных нагрузок. Единичная нагрузка прикладывается в той точке конструкции перемещение которой определяем и действует в направлении ис-комого перемещения. Если определяется линейное перемещение, то прикладывает единичную силу, а если угловое - единицу момента сил.
конструкции при действии реальных нагрузок. Единичная нагрузка прикладывается в той точке конструкции перемещение которой определяем и действует в направлении ис-комого перемещения. Если определяется линейное перемещение, то прикладывает единичную силу, а если угловое - единицу момента сил.
Действующая на конструкцию единичная нагрузка, которая представляет собой вторую систему нагрузок, вызывает возникновение реакций опор и внут-ренних усилий, которые обозначим через 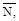
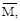
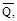
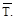 Вместе с единичной наг-рузкой и реакциями опор они образуют систему сил, которая находится в рав-новесии. Если конструкции предать малую возможную деформацию, в качест-ве которой возьмем действительные деформации конструкции, создаваемые пе-
Вместе с единичной наг-рузкой и реакциями опор они образуют систему сил, которая находится в рав-новесии. Если конструкции предать малую возможную деформацию, в качест-ве которой возьмем действительные деформации конструкции, создаваемые пе-
рвой системой нагрузок, то возможная работа внешних сил будет представлять
собой только работу, совершаемую самой единичной нагрузкой. Эта возмож-ная (виртуальная) работа равна произведению единичной нагрузки на переме-щение 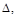 которое совершает точка её приложения; таким образом:
которое совершает точка её приложения; таким образом:
Авнш=1 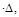
Где величина 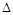 представляет собой искомое перемещение точки конструкции за счёт реальной нагрузки.
представляет собой искомое перемещение точки конструкции за счёт реальной нагрузки.
Возможная работа внутренних сил представляет собой работу, совершае-мую этими силами ( 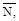
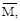
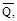
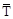 ) при возможной деформации элементов конс-трукции. Эти деформации выбираем такими же, как и действительные дефор-
) при возможной деформации элементов конс-трукции. Эти деформации выбираем такими же, как и действительные дефор-
мации, возникающие при действии на конструкцию реальных нагрузок. Обоз-начая эти деформации через 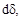
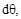
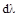 и
и 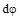 (рис. 12.2 при растяжении (а), из-гибе (б), сдвиге(в), кручении (г)), получим следующие выражения для работы внутренних сил:
(рис. 12.2 при растяжении (а), из-гибе (б), сдвиге(в), кручении (г)), получим следующие выражения для работы внутренних сил:
Ивнт=∫ 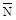
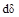 +∫
+∫ 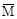
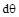 +∫
+∫ 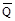
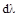 +∫
+∫ 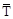
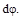
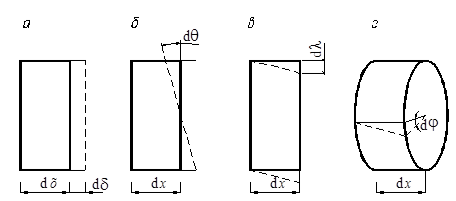
Рис. 12.2
Приравняв, выражение для работ внешних и внутренних сил получаем:
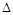 =∫
=∫ 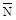
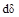 +∫
+∫ 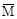
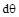 +∫
+∫ 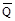
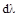 +∫
+∫ 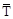
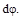
Если деформации малые упругие (справедлив закон Гука), а внутренние усилия в первой системе реальных нагрузок обозначить через NF, MF, QF и TF, то деформации элемента можно записать:
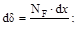
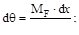
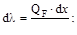
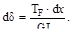
Первое из этих выражений даёт удлинения элемента при действии нормальной силы NF, а последующие деформации при изгибе, сдвиге и круче-нии.
В окончательном виде метод Мора имеет вид
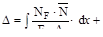
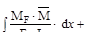
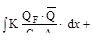
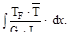
Входящий в формулу К- числовой коэффициент, зависящий от формы поперечного сечения бруса.
Порядок определения перемещений можно кратко изложить следующим образом:
1) разделив конструкцию на участки записываем аналитические выраже-ния для внутренних силовых факторов, на каждом участке, вызванных систе-мой реальных нагрузок- NF, MF, QF, TF;
2) в точке, перемещение которой хотим определить, в направлении иско-мого перемещения приложим единичную нагрузку и определяем внутренние силовые факторы, возникающие в поперечных сечениях, только от этой едини-чной нагрузки (и возникших реакций). При этом необходимо, чтобы правила знаков и направление обхода участков в п.п 1и 2 были бы те же самые.
3) подставить найденные значения в интегралы Мора и выполнить инте-грирование по всей конструкции и просуммировать результаты для получения величины перемещения 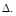 Если результат получен со знаком “минус”, то это означает, что направление искомого перемещения противоположно направле-нию единичной нагрузки.
Если результат получен со знаком “минус”, то это означает, что направление искомого перемещения противоположно направле-нию единичной нагрузки.
Не все члены интегралов Мора могут понадобиться. Так при расчёте ферм только слагаемые, содержащие нормальные силы необходимо учитывать, а для балки или плоской рамы существенными будут только деформации изги-ба и уравнение упрощается:
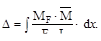
Такие интегралы можно вычислить для каждого элемента конструкции (участка), а затем просуммировать полученные результаты.
При вычислении интеграла Мора, как правило, рассматриваются такие элементы конструкций в которых жёсткости (EA, EJ, GJр) остаются постоянны-ми. Следовательно их можно вынести из под интегралов, после чего все подин-тегральные члены уравнения имеют форму произведений, скажем:
∫ МF 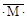 dx.
dx.
В 1925 г. студент Московского института железнодорожного транспорта А.Н. Верещагин предложил упрощение вычислений с использованием форму-лы Мора для стержневых систем, состоящих из прямых участков с постоянной (в пределах каждого участка) жёсткостью. Упрощение базируется на том, что эпюры от единичных нагрузок оказываются линейными.
Допустим, на участке длинной l нужно взять интеграл.
 J=
J= 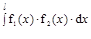
при условии, что f2(x)- линей-ная функция.
f2(x)=b+kx.
Тогда:
J= 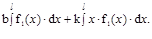
 Первый из интегралов предста-вляет собой площадь, ограни-ченную кривой f1(x) (рис. 12.3 а), которую обозначим
Первый из интегралов предста-вляет собой площадь, ограни-ченную кривой f1(x) (рис. 12.3 а), которую обозначим 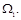 Вто-рой интеграл представляет со-бой статический момент этой площади относительно оси y, т.е.
Вто-рой интеграл представляет со-бой статический момент этой площади относительно оси y, т.е. 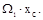
где хс- координата центра тяже-
Рис. 12.3 сти первой эпюры.
Итак, J= 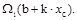 Так как b+kxc=f2(xc) (рис. 12.3 б), то
Так как b+kxc=f2(xc) (рис. 12.3 б), то
J= 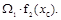
Операция интегрирования заменяется перемножением площади первой эпюры на ординату второй (линейной) эпюры под центром тяжести первой.

 Встречающиеся на практике эпюры могут быть расслоены на простей-шие фигуры: прямоугольник, треугольник, параболу, для которых величина площади и положение центра тяжести (рис. 12.4) известны.
Встречающиеся на практике эпюры могут быть расслоены на простей-шие фигуры: прямоугольник, треугольник, параболу, для которых величина площади и положение центра тяжести (рис. 12.4) известны.

Рис.12.4
Определение перемещений от симметричного и обратно симметричного воздействия надо вести раздельно, проводя вычисления только для половины
системы. Из свойства её симметрии вытекает важное правило: если при “перем-
ножении” эпюр одна из них симметрична, а другая обратно симметрична, то их “ произведение”(премещение)равно нулю.
Если жёсткость стержня переменная, то эпюру усилий от внешних воз-действий надо привести к одной жёсткости, умножая её ординаты 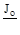 , где Jo- момент инерции одного из сечений.
, где Jo- момент инерции одного из сечений.
12.3 Канонические уравнения
Основная система с заданной нагрузкой и лишними неизвестными, экви-валентна заданной статически неопределимой системе. Следовательно, пере-мещения 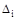 по направлению каждой неизвестных сил Хi от заданной нагрузки и всех неизвестных усилий в лишних связях должны равняться нулю.
по направлению каждой неизвестных сил Хi от заданной нагрузки и всех неизвестных усилий в лишних связях должны равняться нулю.
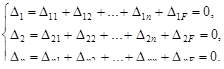
Для линейно деформируемых систем перемещение пропорционально си-ле, его вызвавшей.
Тогда:
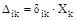
где: 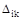 - перемещение в направлении i-той силы, вызванное к-той силой;
- перемещение в направлении i-той силы, вызванное к-той силой; 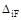 -то же от внешней нагрузки;
-то же от внешней нагрузки; 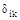 - перемещение в основной системе, соответст-вующее силе Хi при действии силы Хк=1:
- перемещение в основной системе, соответст-вующее силе Хi при действии силы Хк=1:
с учётом сказанного
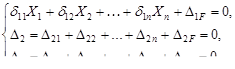
Уравнения имеют стационарную (каноническую) форму, одинаковую для всех статически неопределимых систем.
Представленная система канонических уравнений метода сил содержит главные коэффициенты при неизвестных (с одинаковыми индексами) и побочные (с разными индексами), при этом 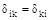 . Величины
. Величины 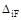 называют свободными членами канонических уравнений.
называют свободными членами канонических уравнений.
Коэффициенты при неизвестных и свободные члены уравнений опреде-ляют по интегралам Мора, а в частных случаях- по правилу Верещагина. Пред-варительно должны быть построены эпюры 
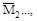
 от единичных наг-
от единичных наг-
рузок 
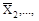
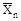 и эпюры MF от заданной нагрузки.
и эпюры MF от заданной нагрузки.
Главные коэффициенты δii всегда положительны. Побочные же коэффи-циенты (перемещения) δiк могут быть положительными, отрицательными или равными нулю.
Коэффициенты и свободные члены подлежат проверке. Универсальная проверка всех коэффициентов при неизвестных состоит, в том что сумма Σδii+ 2Σδiк, представляющая собой условное перемещение по направлению всех не-известных от всех единичных сил 
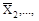
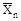 , должна быть равна величине
, должна быть равна величине
δss= 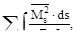
где: Ms= 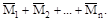
Чтобы возможные ошибки, допущенные при построении единичных эпюр, не перенесли на эпюру 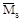 и не свести тем самым на нет всю проверку, следует строить эпюру
и не свести тем самым на нет всю проверку, следует строить эпюру 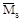 независимо от
независимо от 
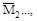
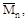 т.е. непосредственно от единичных сил
т.е. непосредственно от единичных сил 
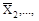
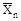 , действующих на основную систему одновре-менно.
, действующих на основную систему одновре-менно.
Если универсальная проверка приводит к недопустимо большому расхо-ждению между суммой контролируемых перемещений и условным перемеще-нием, то для нахождения ошибки можно произвести построчные проверки, ко-торые состоят в том, что сумма коэффициентов при неизвестных каждого уравнения δi1+δi2+…+δin должна быть равна величине:
δis= 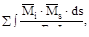
Если построчные проверки дают расхождения только в одной строке, то ошибка связана с вычислением главного коэффициента этой строки. Если же расхождения наблюдаются одновременно в двух строках, то ошибка скорее всего допущена при вычислении того побочного коэффициента, который вхо-дит в обе строки.
Проверка свободных членов уравнений состоит в том, что их сумма 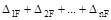 должна быть равна величине
должна быть равна величине
ΔsF = 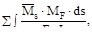
После проверки коэффициентов при неизвестных и свободных членов
канонических уравнений производят их решение и находят 
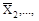
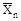 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|