
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Построение эпюр внутренних усилий
12.4 Построение эпюр внутренних усилий
Для построения эпюры моментов в статически определимой системе мо-жно использовать зависимость:
М= 
Существует так называемая кинематическая проверка, состоящая в про-верке равенства нулю условного перемещения основной, или, что то же, задан-ной системы по направлению всех неизвестных от всех неизвестных и заданной нагрузки, т.е.
ΔS = 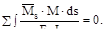
Должны выполнятся и отдельные условия:
Δi = 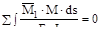 (i=1,2…,n).
(i=1,2…,n).
Эти условия называют деформационной проверкой, суть которой состоит в том, что перемножают окончательную эпюру изгибающих моментов Mz и одну из единичных эпюр изгибающих моментов Mi, определяя при этом перемещение в i-той лишней связи, зная, что оно должно быть равным нулю.
Эпюры поперечных сил Q и продольных сил N строятся для основной системы с заданной нагрузкой и вычисленными неизвестными. В то же время для построения эпюры Q можно использовать заданную нагрузку и эпюру М и рассматривать равновесие отдельных стержней. Для построения эпюры N можно использовать заданную нагрузку и эпюру Q и рассматривать равновесие узлов.
Проверка эпюр Q и N состоит в том, что для любой отсечённой части рамы суммы проекций на две оси внешних и внутренних сил должна равняться нулю (статическая проверка).
Для определения перемещения любой точки статически неопределимой
системы достаточно образовать основную систему и в точке, перемещение ко-торой необходимо определить, приложить единичную нагрузку в направлении искомого перемещения. Построив эпюру изгибающих моментов от этого воз-действия в любой основной системе, следует перемножить её с окончательной эпюрой изгибающих моментов статически неопределимой системы. Если пере-мещение получено со знаком “минус”, то действительное направление переме-щения противоположно направлению единичной нагрузки.
12.5 Практикум
Примеры 1. Определить прогиб Vс и угол поворота φс в точке С балки, считая
жёсткость сечения балки постоянной (EJz=const).
 Определяем реакции в опорах ис-пользуя симметрию расчётной схе-мы, то
Определяем реакции в опорах ис-пользуя симметрию расчётной схе-мы, то
RA=RB= 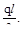
 Балка имеет два участка. На левом участке:
Балка имеет два участка. На левом участке:
 MF=RАx-
MF=RАx- 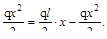
Эпюра MF представлена на (рис. б).
Для определения вертикального перемещения в точке С приложим единичную силу в вертикальном
направлении (рис. в).
 На левом участке изгибающий момент определяем рассмотрев, как и первом случае левую часть балки
На левом участке изгибающий момент определяем рассмотрев, как и первом случае левую часть балки
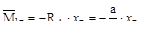
На правом участке

Подставив в интеграл Мора полученные аналитические выражения, имеем:
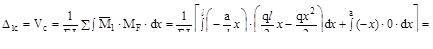
= 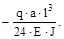
Полученное перемещение отрицательно, следовательно точка С перемес-тилась вверх ( в направлении противоположном вектору единичной силы).
Для определения угла поворота в сечении С следует в этом сечении при-ложить единичную нагрузку в виде момента. На левом участке выражение для изгибающего момента от единичного имеет вид:
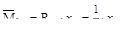
а на правом участке 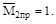
С учётом того, что MFпр=0, в интегралах Мора будет только одно слагае-мое:
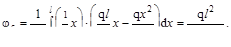
Угол поворота φс > 0, т.е. поворот совершён в направлении М2 (против хода часовой стрелки).
Воспользовавшись способом Верещагина для получения прогиба Vc не-обходимо площадь грузовой эпюры MF умножить на ординату единичной эпюры 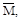 под центром тяжести параболической эпюры MF
под центром тяжести параболической эпюры MF
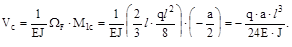
Для угла поворота φс следует перемножить MF 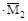
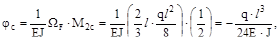
где:  и
и 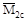 - значения первой и второй (соответственно) единичных эпюр под центром тяжести грузовой эпюры MF. Слагаемое для правого участка рав-ны нулю, поскольку MFпр=0. На рис. б, в, г, даны эпюры MF,
- значения первой и второй (соответственно) единичных эпюр под центром тяжести грузовой эпюры MF. Слагаемое для правого участка рав-ны нулю, поскольку MFпр=0. На рис. б, в, г, даны эпюры MF, 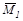 и
и 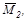 а на ри-сунке д - форма изогнутой оси балки.
а на ри-сунке д - форма изогнутой оси балки.
2. Способом Верещагина определить вертикальное перемещение сечения А и угол поворота сечения В если Е =2·105 МПа, J =2·103 см4.
Построим эпюру MF (рис. б) известным способом и представим ее «расслоенной» (рис. в) на простейшие площадки: прямоугольник с центром тяжести С1, треугольники с центром тяжести С2 и С4 и параболический сегмент высотой 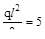 , с центром тяжести С3.
, с центром тяжести С3.
На рис. г показана эпюра 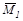 , полученная в результате нагружения еди-ничной силой F=1, приложенной в точке А и обозначены значения ηi под цент-рами тяжести каждой из простейших площадок.
, полученная в результате нагружения еди-ничной силой F=1, приложенной в точке А и обозначены значения ηi под цент-рами тяжести каждой из простейших площадок.
На рисунке д показана эпюра 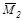 , полученная в результате нагружения
, полученная в результате нагружения
единичной парой сил М=1, приложенной в сечении В.

 Поскольку центр тяжести прямоугольника находится на расстоянии 0,5 м от точки А, то η1=
Поскольку центр тяжести прямоугольника находится на расстоянии 0,5 м от точки А, то η1=  (см. рис. г). Определить значение осталь-ных η2, η3, η4 для участка ВС из уравнения
(см. рис. г). Определить значение осталь-ных η2, η3, η4 для участка ВС из уравнения 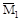 = l·х, задавая в каждом случае координаты С2, С3 и С4 в системе коор-динат, имеющих начало в край-ней левой точке или вычислив приращения ηi на участке ВС.
= l·х, задавая в каждом случае координаты С2, С3 и С4 в системе коор-динат, имеющих начало в край-ней левой точке или вычислив приращения ηi на участке ВС.



 С учетом этого опреде-лим прогиб балки в сечении А:
С учетом этого опреде-лим прогиб балки в сечении А:

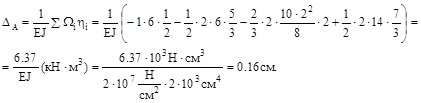
Знак “минус” в формуле ставится в том случае, когда грузовая эпюра МF и ордината единичной эпюры 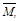 находятся по разные стороны базовой линии эпюр.
находятся по разные стороны базовой линии эпюр.
Для определения угла поворота в сечении В приложим в этом сечении единичную пару сил М=1, построим эпюру 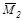 (рис. д) и перемножим МF·
(рис. д) и перемножим МF· 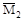 .
. 
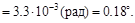
Оба значения и VA и φВ получены со знаком “плюс”, следовательно точ-ка А переместилась вниз, а сечение В повернулось против часовой стрелки (в том же направлении, что и приложенные единичные нагрузки).
Примеры раскрытия статической неопределимости рам с использованием метода сил и способа Верещагина даны в разделе V.
Вопросы для повторения
1. Что называют статически определимыми и статически неопредели-мыми системами?
2. Что называется степенью статической неопределимости системы?
3. Как определяется степень статической неопределимости?
4. Что представляет собой основная система?
5. В чём заключается выбор основной системы?
6. Что выражает каждое из канонических уравнений?
7. Каков физический смысл произведений 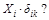
8. Какие перемещения называют главными и побочными. Какими свой-ствами они обладают?
9. В каком порядке производится расчёт статически неопределимых сис-тем?
10. Перемножением каких эпюр определяют коэффициенты и свободные члены системы канонических уравнений?
11. Как определяются значения неизвестных Хi?
12. Какими приёмами можно построить окончательную (суммарную) эпюру изгибающих моментов?
13. Как производится статическая проверка правильности раскрытия ста-тической неопределимости системы?
14. Как проводят деформационную проверку правильности построения окончательной эпюры М статически неопределимой системы?
15. Как производится определение перемещений в статически неопреде-лимых системах?
16. Какие системы называют геометрически неизменяемыми?
 Тесты для повторения
Тесты для повторения
1. Степень статической неопределимости заданной рамы равна
(а) 1; (б) 2; (в) 3; (г) 4.
Ответ: (в). Для равновесия (геометрической неиз-меняемости) достаточно трёх связей, а опоры накла-дывают шесть связей, т.е. три- избыточные (лиш-ние).
Решение можно получить и по формуле(см. 12.1)
К=ЗД-2Ш-С (*)
К= 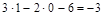 -трижды статически неопределимая система.
-трижды статически неопределимая система.
2. Степень статической неопределимости заданной рамы равна:
(а) 5; (б) 2; (в) 3; (г) 4.
 Ответ: (г). Система дважды статически нео-пределима внешне, замкнутый контур увеличи-вает на 3 степень неопределимости, а простой шарнир С- уменьшает на единицу, т.о.
Ответ: (г). Система дважды статически нео-пределима внешне, замкнутый контур увеличи-вает на 3 степень неопределимости, а простой шарнир С- уменьшает на единицу, т.о.
К=2+3-1=4.
Если провести анализ по формуле (*), то число дисков-1, простых шарниров в системе-1, число опорных стержней (внешних связей) - 5.
К= 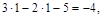
т.о. система четырежды статически неопределима.
 3. Укажите неправильный вариант основной системы для заданной статически неопределимой рамы.
3. Укажите неправильный вариант основной системы для заданной статически неопределимой рамы.
Ответ: (г), поскольку система представляет в этом
 случае “мгновенный механизм” (не может противодействовать повороту относительно левого шарнира).
случае “мгновенный механизм” (не может противодействовать повороту относительно левого шарнира).

 4. Укажите неправильный вариант основной системы для заданной статически неопределимой рамы.
4. Укажите неправильный вариант основной системы для заданной статически неопределимой рамы.
Ответ: (г) поскольку данная система - механизм может перемещаться в горизонтальной плоскости.

 5. Задана статически неопределимая балка (рис. а), принята её эквивалентная система (рис. б), построены грузовая МF и единичная
5. Задана статически неопределимая балка (рис. а), принята её эквивалентная система (рис. б), построены грузовая МF и единичная 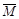 эпюры изгибающих мо-ментов в основной системе. Чему равно значение Х1?
эпюры изгибающих мо-ментов в основной системе. Чему равно значение Х1?
(а) 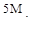 (б)
(б) 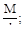 (в)
(в) 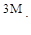 (г)
(г) 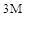
Ответ: (а). Каноническое уравнение метода сил для один раз статически неопределимой системы
δ11Х1+∆1F=0.
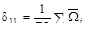 ·
· 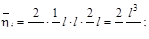
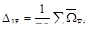
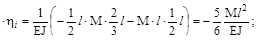
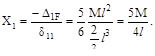
6. Задана статически неопределимая балка, построена её окончательная эпюра М изгибающих моментов. Укажите изогнутую ось балки.



Ответ: (в), поскольку только у этой изогнутой оси нет поворота сечения в за-делке и на левой части выпуклость “вверх” соответствует зоне растянутых “во-локон” на эпюре, а правая часть эпюры свидетельствует о том, что растянуты нижние “волокна”.
Контрольные тесты
1.Укажите пару коэффициентов канонических уравнений, равных между собой:
(а) δ11 и δ12; (б) δ23 и δ32; (в) δ22 и δ33; (г) δ31 и δ23.
2. Коэффициенты канонических уравнений δik (i 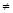 k) могут быть:
k) могут быть:
(а) δik >0; (б) δik < 0; (в) δik ≥0; (г) δik> = < 0.
3. Степень статической неопределимости заданной рамы равна:

(а) 4; (б) 3;
(в) 2; (г) 1.
 4. Степень статической неопределимости заданных рам равна (установите соот-ветствие)
4. Степень статической неопределимости заданных рам равна (установите соот-ветствие)

(д) 4; (е) 5; (ж) 6; (з) 7.
 5. Укажите неправильный вариант основной систе-мы для заданной статически неопределимой рамы.
5. Укажите неправильный вариант основной систе-мы для заданной статически неопределимой рамы.


6. Укажите правильный вариант основной системы для заданной статически неопределимой рамы.



7. Чему равен прогиб в точке А?
 (а)
(а) 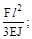 (б)
(б) 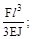
(в) 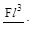 (г)
(г) 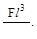
8. Количество канонических уравнений равно числу:
(а) внешних лишних связей системы;
(б) внутренних (взаимных) лишних связей системы;
(в) внешних и внутренних лишних связей системы;
(г) независимых уравнений статики для заданной системы.
9. Для статически неопределимой балки (рис.а) выбрана эквивалентная система (рис. б). Чему равно усилие Х1?

(а) 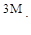 (б)
(б) 
(в) 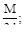 (г)
(г) 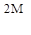

10. Для статически неопределимой балки (рис. а) принята эквивалентная система (рис. б), записано каноническое уравнение: 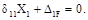 Что представляет собой ве-личина
Что представляет собой ве-личина 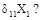
(а) прогиб в точке А от Х1 в основной системе;
(б) угол поворота сечения С от Х1 в основной системе;
(в) угол поворота сечения С от единичного момента, действующего в направлении Х1 в основной системе;
(г) угол поворота в сечении В от Х1 в основной системе.
11. Задана статически неопределимая балка (рис. а), принята её эквивалентная система (рис. б), построены грузовая МF и единичная 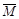 эпюры изгибающих моментов в основной системе. Чему равно значение Х1?
эпюры изгибающих моментов в основной системе. Чему равно значение Х1?

(а) 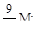 (б)
(б) 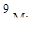
(в) 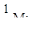 (г)
(г) 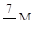
 12. Дана статически неопределимая рама (рис. а), её эквивалентная система (рис. б), изображены грузовая МF и единичная
12. Дана статически неопределимая рама (рис. а), её эквивалентная система (рис. б), изображены грузовая МF и единичная 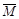 эпюры изгибающих моментов в основной системе. Жёсткость на всех участках постоянна (EJ=const). Чему равно
эпюры изгибающих моментов в основной системе. Жёсткость на всех участках постоянна (EJ=const). Чему равно 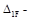 перемещение в направлении Х1, вызванное внешней нагрузкой?
перемещение в направлении Х1, вызванное внешней нагрузкой?

(а) 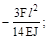 (б)
(б) 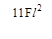 (в)
(в) 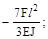 (г)
(г) 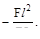
13. Укажите правильную окончательную эпюру изгибающих моментов для за-данной статически неопределимой балки.


14. Задана статически неопределимая балка, построена её окончательная эпюра М изгибающих моментов. Укажите изогнутую ось балки:



|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|