Поверочные и проектные расчеты

10.4. Поверочные и проектные расчеты

Для обеспечения прочности бруса необходимо, чтобы наибольшие растягивающие и наибольшие сжимающие напряжения в опасном сечении, где момент имеет наибольшее значение (рассматриваются только балки с постоянным по всей длине поперечным сечением), не превосходили соответствующих допускаемых напряжений.

Обозначим h_t – расстояние до наиболее удаленного от нейтральной оси растянутого волокна, h_c – расстояние до наиболее удаленного сжатого волокна. Тогда наибольшее растягивающее напряжение

σ_xt _m_ах = (M_zh_t)/I_z ;

наибольшее сжимающее напряжение (взятое по абсолютному значению)

σ_xc _m_ах = (M_zh_c)/I_z.

Для хрупких материалов допускаемые напряжения на растяжение и сжатие различны: σ_c _adm в несколько раз больше σ_t _adm. Поэтому для балок из таких материалов обычно подбирают сечения, не симметричные относительно нейтральной оси. При этом сечение ориентируют таким образом, чтобы h_t < h_c, т.е. чтобы обеспечивалось неравенство max σ_xt<max σ_xc. В таких случаях применяются два условия прочности:

σ_{xt max} = (M_zh_t)/I_z ≤ σ_{t adm};

σ_{xc max} = (M_zh_c)/I_z ≤ σ_{c adm},

Если сечение балки симметрично относительно нейтральной оси (такие сечения целесообразно применять для балок из пластичных материалов, имеющих одинаковые величины σ_adm на растяжение и сжатие), т.е. h_t= h_c= h/2, условие прочности имеет вид

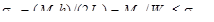
Величина W_z называется моментом сопротивления изгибу поперечного сече-ния. Для прямоугольника

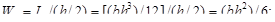
для круга

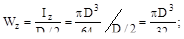
для кольца

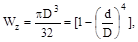
где D(d) – диаметр наружной (внутренней) окружности.

Для прокатных профилей значения моментов сопротивления указаны в таблицах сортамента.

Допускаемый изгибающий момент определяется по формуле

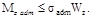
Найдя M_z _adm и зная связь между М_z и нагрузкой, можно определить допуска-емую нагрузку.

Для подбора сечения бруса используется зависимость

W_z ≥ M_z /σ_adm.

Условие прочности по касател ьным напряжениям имеет вид

τ_мах≤ τ_adm.

Главные напряжения (см. п.4.2) следует проверять (σ_red ≤ σ_adm) в сечениях, где одновременно имеют большие значения и изгибающий момент (определяющий σ_х), и поперечная сила (определяющая τ_ху), в точках, в которых напряжения σ_х и τ_ху достигают значительных величин.

При подборе сечений брусьев стремятся удовлетворить условиям прочности при наименьшем расходе материала, пропорциональном площади сечения, если последняя сохраняется постоянной. Значит, чем больше момент сопротивления при одной и той же площади, тем рациональнее сечение.

Поскольку наибольшие нормальные напряжения при изгибе действуют в слоях, удаленных от оси бруса, то стандартные прокатные профили (двутавр, швеллер) наиболее экономичны. Для этих профилей характерна концентрация материала в периферийных зонах, где напряжения имеют наибольшие значения. Вблизи оси бруса (зона минимальных напряжений) находится лишь незначительная часть материала, что необходимо для работы сечения как единого целого. По этой же причине балка круглого сечения будет весьма нерациональна.

Отношением W_z /A = kh можно оценить степень экономичности профиля при сохранении постоянной высоты сечения h. Для прямоугольника

W/A = [(bh²/6)]/(bh) = 0,17h .

Для круга k = 0,125; для прокатных двутавров k = 0,29...0,31; для прокатных швеллеров k = 0,27...0,31. Для балки прямоугольного сечения при фиксированной площади выгодно (до известных пределов) увеличивать h. Однако высокие, но узкие профили обладают малой жесткостью относительно другой главной оси и неустойчивы при изгибе.

При различном сопротивлении материала растяжению и сжатию наиболь-шего эффекта можно достичь, используя несимметричное относительно оси z сечение, о чем говорилось выше.

10.5 Перемещение при изгибе. Метод начальных параметров.

При нагружении балки ось балки искривляется. Точки оси получают по-перечные перемещения, а попереч-ные сечения совершают поворот от-носительно своих нейтральных осей. Изогнутую ось балки называют упру-гой линией. Углы поворота сечений φ могут быть определены и как углы наклона касательных к упругой линии в данном сечении (рис. 10.8).

Рис. 10.8

Линейные V и угловые φ перемещения являются функциями координаты х. В силу малости углов поворота имеет:

φ(х)

Из курса математического анализа известно, что кривизна плоской кривой V(х) может быть определена по формуле:

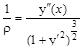Поскольку величина 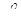величина малая по сравнению с единицей, то упрос-тив последнее выражение можно записать приближённое дифференциальное уравнение:

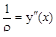С учётом ранее полученного при изгибе выражения:

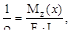
имеем, EI_z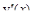=M_z(x),

где: I_z- момент инерции поперечного сечения балки, относительно её нейт-ральной оси z;

Е- модуль продольной упругости материала;

EI_z- изгибная жёсткость.

В общем случае для определения функции прогибов и углов поворота не-обходимо проинтегрировать последнее уравнение и определить константы интегрирования из граничных условий –условий закрепления на опорах. В случае двухопорной балки – это равенство нулю перемещений над опорами, а в случае жёсткого защемления – равенство нулю и угла поворота, и перемещения в заделке.

Для балки, имеющей несколько участков, решение существенно осло-жняется, поскольку на каждом участке функция M_z(x) имеет иное аналитичес-кое выражение и необходимо на границах соседних участков обеспечить непрерывность функций φ(х) и V(х). Это приводит к тому, что для балки, име-ющей n участков из числа 2n граничных условий получать 2n алгебраических

уравнений и решая эту систему находить 2n постоянных интегрирования.

Для балок постоянной жесткости ( EI_z=const) можно свести решение к нахождению только двух констант интегрирования при любом количестве участков. Это возможно в случае, когда в аналитических выражениях для мо-ментов или прогибов при переходе к следующему участку повторялись все члены предыдущего участка, а вновь появляющиеся слагаемые обращаются в нуль на границе нового участка.

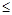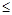Рассмотрим балку, нагруженную силовыми воздействиями, вызывающи-ми вертикальные перемещения в положительном направлении оси у (рис. 10.9). Начало координат поместим в крайнюю левую точку оси балки, и оно будет общим для любого участка. Выражения для изгибающих моментов M_z(х) будем состав-лять, рассматривая в равнове-сии левую часть балки. Запи-шем уравнение для пятого участка (d x l)

M_z(x)=M(x-a) +F(x-b)+

q .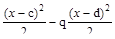

Для обеспечения рекуррентно-

сти для пятого участка введена

Рис.10.9 “компенсирующая” распределён-ная нагрузка, поскольку сохранив предпоследнее слагаемое (мы как бы продлили распределённую нагрузку и на пятый участок) следует обеспечить действительное силовое воздействие. В первом слагаемом сомножителем введена (х-а) =1. Размеры a, b, c, d соответствуют координате приложения внешних воздействий.

Легко убедиться, что для любого участка M_z(х) можно получить, сох-ранив в уравнении слагаемые, расположенные левее проведенного на участке сечения.

Дважды проинтегрировав последнее выражение, получим:

E 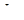V(x) = c₁+c₂x+ .

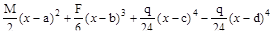Постоянные интегрирования С₁и С₂ по своей сути означают:

С₁=E С₂=E 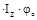- прогиб V 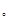и угол поворота сечения φ 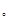в начале ко-ординат (х = 0), умноженные на жёсткость сечения при изгибе. Эти постоян-ные определяются из граничных условий. Если начало координат совпадает с жёсткой заделкой, то φ 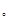= 0, V 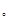= 0. Если начало координат совпадает с левой

опорой, то прогиб V =0, а вторую константу определяют из условия равенства

нулю прогиба на правой опоре.

Выявив составляющие от различных внешних силовых факторов мож-но записать универсальное уравнение упругой линии балки.

EI_zV=EI_zV_◦+EI_zφ_◦x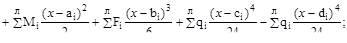

где: M_i, F_i, q_i – внешние нагрузки, включающие и опорные реакции, располо-женные левее (знак ”л” над знаком суммы) от рассматриваемого сечения;

a_i, b_i, c_i, d_i – расстояния от начала координат до сечения, где приложена данная нагрузка;

V- перемещение центра тяжести сечения по направлению, перпендикуляр-ному оси балки х.

Углы поворота легко получить дифференцированием функции прогибов. Величины φ , 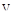называют начальными параметрами, что и определило назва-ние метода.

Построив упругую линию по расчётным значениям прогибов в несколь-ких сечениях проверяют, выполняется ли условие жёсткости:

V_max 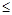V_adm;

где: V_adm назначается как (0.01 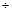0.001) длины пролёта балки и принимается в зависимости от назначения этой конструкции.

Если прочность балки обеспечена, а условие жёсткости не выполнено, то следует подобрать размеры сечения такими, чтобы обеспечить и жёсткость. К примеру если V_max=1.5V_adm, то момент инерции нового сечения должен быть в полтора раза больше момента инерции прежнего сечения.

⇐ Предыдущая 37 38 39 40 414243 44 45 46 Следующая ⇒