
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Построение ФСР для системы по корням характеристического уравнения.
2.17.Системы ЛОДУ с постоянными коэффициентами. Характеристическое уравнение. Построение общего решения по корням характеристического уравнения (вывод для случая вещественных различных корней).
Система ЛОДУ с постоянными коэффициентами:
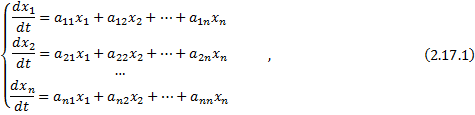
где 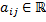 ;
; 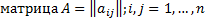 .
.
Матричная форма:

Найдем решение вида 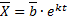 , где
, где 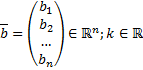 .
.
Подставим в 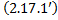 :
:

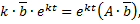
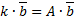 ,
,
т.е. 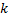 - собственное значение матрицы
- собственное значение матрицы 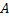 ;
; 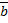 – соответствующий собственный вектор.
– соответствующий собственный вектор.
Опр. Характеристическим уравнением системы ЛОДУ с постоянными коэффициентами  называется характеристическое уравнение
называется характеристическое уравнение 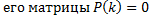 , где
, где 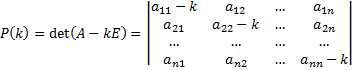 .
.
Построение ФСР для системы по корням характеристического уравнения.
1. Случай различных действительных корней.
Пусть 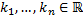 - различные корни характеристического уравнения (т.е. собственные значения матрицы
- различные корни характеристического уравнения (т.е. собственные значения матрицы 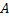 ),
),
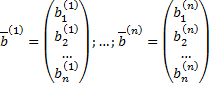 – соответствующие собственные вектора.
– соответствующие собственные вектора.
Тогда вектор-функции 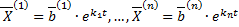 образуют ФСР для системы
образуют ФСР для системы 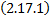 .
.
Док-во: нужно доказать, что частные решения 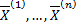 линейно независимы.
линейно независимы.
Вронскиан 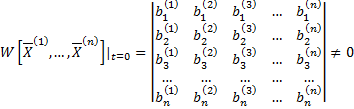 , т.к. собственные вектора
, т.к. собственные вектора 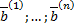 линейно независимы (как собственные вектора, соответствующие различным собственным значениям), т.е. столбцы матрицы линейно независимы.
линейно независимы (как собственные вектора, соответствующие различным собственным значениям), т.е. столбцы матрицы линейно независимы.
 .
.
Пример.
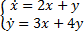 .
.
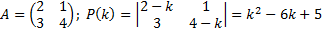
(можно использовать, что для матрицы 2Х2 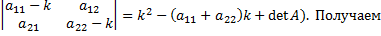

Найдем собственные значения.
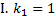 ; собственный вектор
; собственный вектор  находим из СЛАУ
находим из СЛАУ
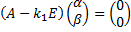 ,
,
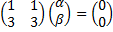 ,
,
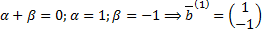 .
.
 ; собственный вектор
; собственный вектор 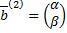 находим из СЛАУ
находим из СЛАУ
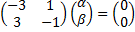 ,
,
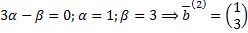 .
.
ФСР: 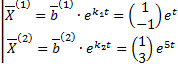 ,
,
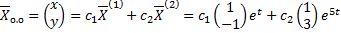 ,
,
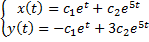 .
.
2. Случай кратных действительных корней.
Пусть 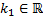 - корень характеристического уравнения кратности
- корень характеристического уравнения кратности 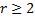 . Ему соответствует решение вида
. Ему соответствует решение вида
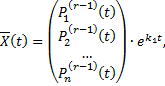
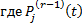 – многочлен степени
– многочлен степени 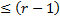 . Коэффициенты находятся методом неопределенных коэффициентов.
. Коэффициенты находятся методом неопределенных коэффициентов.
Пример.
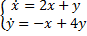

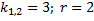
Ищем решение в виде 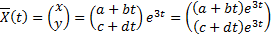
Подставим в систему:
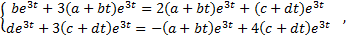
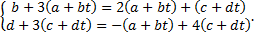
Коэффициент при 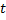 в 1-м уравнении:
в 1-м уравнении: 
Коэффициент при  в 1-м уравнении:
в 1-м уравнении: 
Коэффициент при 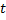 во 2-м уравнении:
во 2-м уравнении: 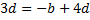
Коэффициент при  во 2-м уравнении:
во 2-м уравнении: 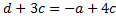 . Получаем СЛАУ
. Получаем СЛАУ
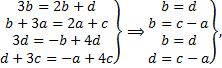
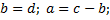
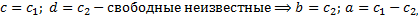

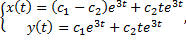
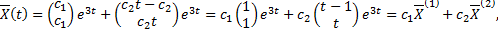
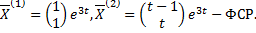
3. Случай комплексных корней кратности 1.
Пусть  – корень кратности 1
– корень кратности 1  . Паре корней
. Паре корней  и
и 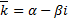 соответствуют 2 линейно независимых решения. Пусть
соответствуют 2 линейно независимых решения. Пусть 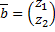 – комплексный собственный вектор, соответствующий комплексному собственному значению
– комплексный собственный вектор, соответствующий комплексному собственному значению 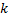 . Он находится из СЛАУ
. Он находится из СЛАУ  .
.
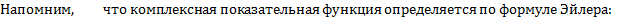
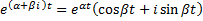 .
.
Тогда корням 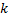 и
и 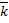 соответствует комплексное решение системы ДУ:
соответствует комплексное решение системы ДУ:
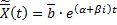
Тогда 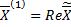 и
и 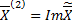 – вещественные линейно независимые решения, соответствующие корням
– вещественные линейно независимые решения, соответствующие корням 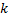 и
и 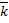 .
.
Пример.
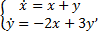
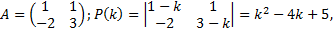
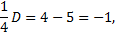
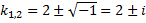 ,
, 
Найдем собственный вектор 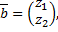 соответствующий
соответствующий 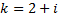 :
:
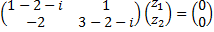 ,
,

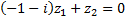 (второе уравнение пропорционально первому с коэффициентом
(второе уравнение пропорционально первому с коэффициентом 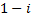 ),
),
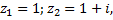
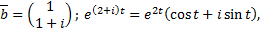
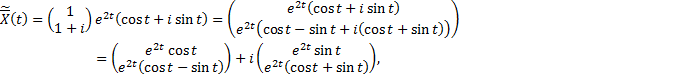
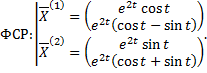
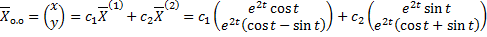 ,
,
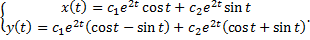
Литература
1. Зарубин В.С., Иванова Е.Е., Кувыркин Г.Н. Интегральное исчисление функций одного переменного: Учеб. для вузов / Под ред. В.С. Зарубина, А.П. Крищенко. - М.: Изд-во МГТУ им. Н.Э. Баумана, 1988.-506 с. (Сер. Математика в техническом университете. Вып. VI).
2. Агафонов С.А., Герман А.Д., Муратова Т.В. Дифференциальные уравнения: Учеб. для вузов / Под ред. В.С. Зарубина, А.П. Крищенко. - М.: Изд-во МГТУ им. Н.Э. Баумана, 1997.- 336 с. (Сер. Математика в техническом университете. Вып. VIII).
3. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. -М., Наука, 1981.
4. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. - М.: Наука, 1981.
5. Филиппов А.Ф. Введение в теорию дифференциальных уравнений. М.:УРСС, 2004.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|