Хелпикс

Главная

Контакты

Случайная статья



Метод вариации постоянных решения неоднородных ЛДУ n-го порядка (вывод для ).

⇐ ПредыдущаяСтр 25 из 28Следующая ⇒


2.13. Метод вариации постоянных решения неоднородных ЛДУ n-го порядка (вывод для ).

 

Пусть 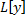 – линейный дифференциальный оператор с переменными коэффициентами. Рассмотрим ЛНДУ:

Соответствующее ЛОДУ:

Общее решение ЛОДУ:

.

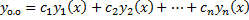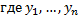 – ФСР ЛОДУ,

 – произвольные постоянные.

Теорема. Общее решение ЛНДУ ( 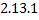) имеет вид

,

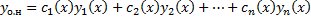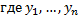 – ФСР соответствующего ЛОДУ,

производные функций  определяются из СЛАУ

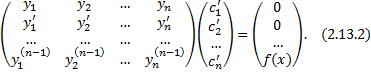
Замечание 1. СЛАУ (2.13.2) имеет единственное решение для 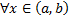, т.к. ее определитель  ( ).

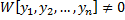Замечание 2.  Функций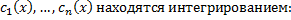

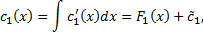
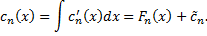
Тогда

,

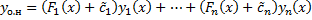 – произвольные постоянные.

Док-во (случай 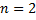). Рассмотрим ЛНДУ

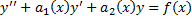
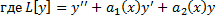 – линейный дифференциальный оператор 2-го порядка.

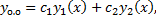
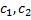 – произвольные постоянные

СЛАУ (2.13.2) имеет вид

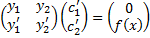, или

.

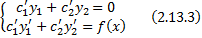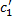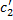1. Покажем, что если  и  удовлетворяют (2.13.3), то функция  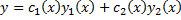– решение ЛНДУ (2.13.1).

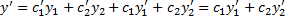
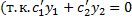 в силу (2.13.3)).

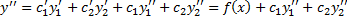
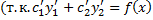 в силу (2.13.3)).

Тогда

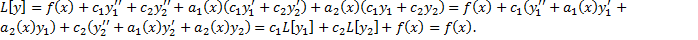
Таким образом 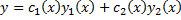 – решение ЛНДУ (2.13.1).

2. Решив СЛАУ (2.13.3), получим решение вида

.

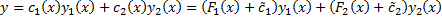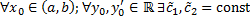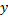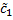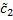Покажем, что для , такие, что решение , соответствующее  и , удовлетворяет начальным условиям

.

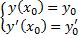Для 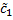 и 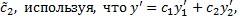 получим систему

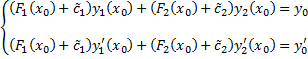
- СЛАУ с определителем 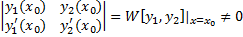, т.к.  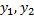– ФСР ЛОДУ,

т.е. 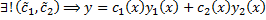 – общее решение.

Пример.

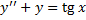
(метод неопределенных коэффициентов неприменим!).

Соответствующее ЛОДУ:

,

,

,

,

,

,

,

 

,

 

 

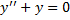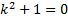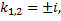
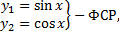
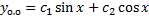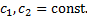
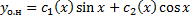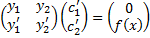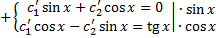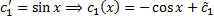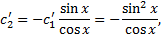
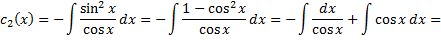
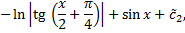
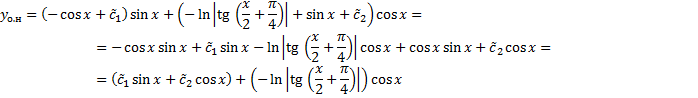
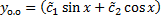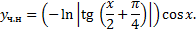
2.14. Нормальные системы ДУ. Задача Коши и теорема существования и единственности ее решения. Сведение ДУ n-го порядка к нормальной системе. Сведение нормальной системы к одному уравнению n-го порядка.

 

(2.14.1) – нормальная система ОДУ.

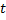 – независимая переменная,

 – неизвестные (искомые) функции,

 – определены в области .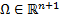

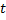Если  не зависят явно от , то система (2.14.1) называется автономной.


⇐ Предыдущая19202122232425262728Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.