Контакты

Случайная статья

Векторная форма записи системы.

⇐ ПредыдущаяСтр 26 из 28Следующая ⇒

Векторная форма записи системы.

Пусть 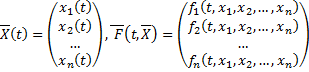. Тогда система (2.14.1) можно записать в виде

Опр. Вектор-функция называется частным решением системы (2.14.1) на 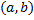, если при ее подстановке в (2.14.1) все уравнения системы (2.14.1) обращаются в тождества на .

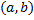Задача Кошидля системы (1).

Найти частное решение , удовлетворяющее начальным условиям

где точка .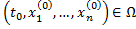

В векторной форме начальные условия имеют вид

где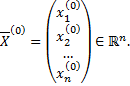

Опр. Семейство вектор-функций , зависящих от 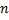произвольных постоянных, называется общим решением системы (2.14.1), если

1. 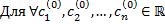вектор-функция является частным решением.

2. Для 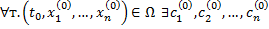такие, что 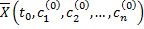удовлетворяет начальному условию (2.14.2).

Векторная форма общего решения -

.

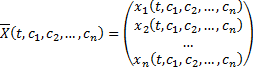Теорема существования и единственности решения задачи Коши для нормальных систем.

Пусть функции и их частные производные 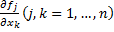непрерывны в области 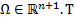огда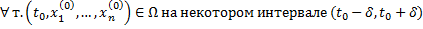

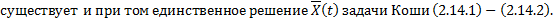
Сведение ДУ n-го порядка к нормальной системе. Рассмотрим ДУ -го порядка

Введем обозначения:

.

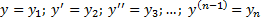Тогда уравнение (2.14.3) равносильно системе

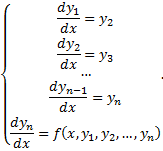
Пример.

.

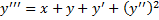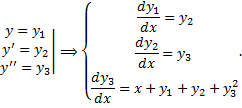
Сведение нормальной системы к одному уравнению n-го порядка.

Рассмотрим случай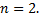

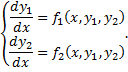
Сведем к ДУ 2-го порядка. Из 1-го уравнения

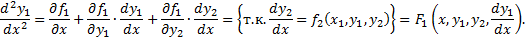
Если из 1-го уравнения системы можно выразить 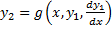, то для 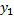получим уравнение 2-го порядка:

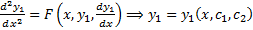(общее решение ДУ 2-го порядка).

Тогда .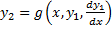

Пример.
.

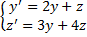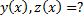
Продифференцируем 1-е уравнение:

.

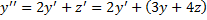Из 1-го уравнения:

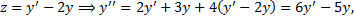
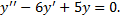
Характеристическое уравнение полученного ЛОДУ с постоянными коэффициентами:

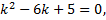
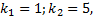
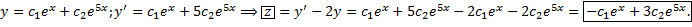
2.15.Автономные системы ДУ. Фазовое пространство и фазовые траектории. Первые интегралы систем ДУ. Симметричная форма записи систем ДУ и ее применение к нахождению первых интегралов.

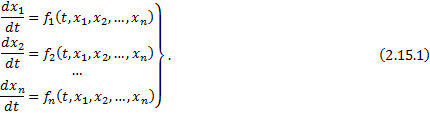
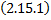– нормальная система ОДУ.

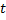– независимая переменная,

– независимые функции,

– определены в области .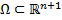

Если не зависят явно от 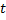, то система (2.15.1) является автономной.

⇐ Предыдущая 19 20 21 22 23 24 252627 28 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.