Какими являются события А1 и А2: зависимыми или независимыми?

⇐ ПредыдущаяСтр 10 из 11Следующая ⇒

??? Какими являются события А1 и А2: зависимыми или независимыми?

А события А₃ и А₄ ?Почему?

??? Какими являются события А1 *А2 и А3 *А4: совместными или

несовместными? Почему?

??? Какими формулами будете пользоваться при вычислении вероятности

таких событий?

Ø Запишите необходимые формулы.

Ø Выразите вероятности каждого из событий, исходя из условия задачи.

Ø Чему равна искомая вероятность?

Ø Произведите необходимые расчёты и найдите искомую вероятность.

??? Отвечает ли этот результат (приблизительно) вашим ожиданиям?

?** Согласны ли вы с решением, данным ниже?

**************************************************************************

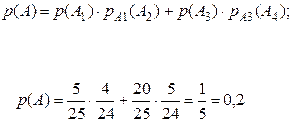Домашнее задание ДЗ-5

Ø В следующих задачах вычислите вероятность события, используя нужное определение вероятности (если это возможно);

Ø используйте, где это удобно, комбинаторные правила и соотношения.

Ø Установите взаимосвязь описываемых событий: являются ли группы событий совместными/несовместными, зависимыми/независимыми, как выражается искомое событие через другие составляющие его события.

Ø Выразите взаимосвязь событий формулой, при необходимости введите нужные обозначения.

Ø Укажите формулы для вычисления вероятности каждого составного события, зная вероятности элементарных событий.

Задача 1.  Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того,что номер наудачу извлеченного жетона не содержит цифры5.

Задача 2. Брошены две игральные кости. Найти вероятность того, что

а) на обеих костях выпадет 6 очков;

б) на обеих костях выпадет одинаковое число очков;

в) на обеих костях выпадет четное число очков.

Задача 3. В студенческой группе учатся 12 девушек и 8 юношей. На конференцию выбирают делегацию из пяти человек. Найти вероятность того, что среди членов делегации будет: а) ровно 3 девушки; б) не менее трех девушек.

Задача 4. На первом этаже семиэтажного дома в лифт вошли 3 человека. Каждый может выйти из лифта на любом этаже (кроме первого). Найти вероятности событий: А – все вышли из лифта на четвертом этаже;

В – все вышли из лифта на одном и том же этаже;

С – все выходили из лифта на разных этажах.

Задача 5. Два друга условились встретиться в Москве у памятника Пушкину между 12 и 13 часами. Договорились, что пришедший первым ждет 20 минут и уходит. Какова вероятность, что друзья встретятся?

Задача 6. В прямоугольник 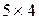см² вписан круг радиуса 1,5 см. Какова вероятность того, что точка, случайным образом поставленная в прямоугольник, окажется внутри круга?

Задача 7. Три орудия ведут огонь по цели, вероятность попадания в которую при одном выстреле из первого орудия 0,5; из второго – 0,6; из третьего – 0,7. Зная, что каждое орудие стреляет один раз, найти вероятность:

а) поражения цели, если для этого достаточно двух попаданий,

б) хотя бы одного попадания в цель.

Задача 8.  В колоде 36 карт. Наудачу вынимают из колоды 2 карты. Определить вероятность того, что вторым вынут туз, если первым тоже вынут туз.

Задача 9.  Из колоды в 36 карт вынимают сразу три карты. Найти вероятность того, что среди них одна дама, одна семерка, один туз.

Задачи-продолжения

Ø Продолжите решение задач из Л-5 (п.5.3)

⇐ Предыдущая 2 3 4 5 6 7 8 91011 Следующая ⇒