а в каждом случае работы блоков 5 и 6 события являются независимыми.

.............................................................................................................................

Ø Как вычислить его вероятность?

..............................................................................................................................

Ø Проверьте себя:

Следовательно, событие .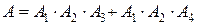

Вероятность события А находится по формуле:

= .

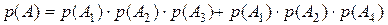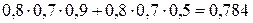2.5.

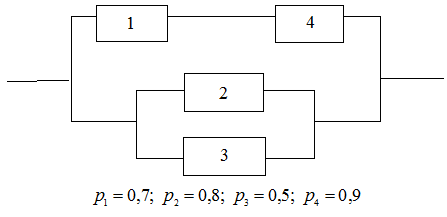
Определите надёжность схемы, представленной на рисунке, где 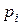- вероятность

безотказной работы

i-того элемента.

(Под надёжностью схемы понимается вероятность безотказной работы схемы.)

Решение. Соединение элементов, представленное на схеме, является комбинированным, так как содержит и последовательное, и параллельное соединение. Напомним, что

при последовательном соединении система работает,

если работают все элементы, соединённые последовательно;

и не работает, когда не работает хотя бы один элемент.

При параллельном соединении система работает,

если работает хотя бы один элемент системы;

и не работает, когда не работает ни один элемент.

Выделим участок схемы, содержащий последовательное соединение элементов (1) и (4) в отдельный элемент (5). Участок схемы, содержащий параллельное соединение элементов (2) и (3), выделим в элемент (6).

Обозначим В – событие, состоящее в том, что элемент (5) работает, 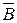- противоположное событие, состоящее в том, что элемент (5) не работает.

Событие С – это безотказная работа элемента (6), - событие состоящее в том, что элемент (6) не работает.

Событие, состоящее в том, что работает вся схема, обозначим А. Так как элементы (5) и (6) соединены параллельно, то для наступления события А необходимо, чтобы работал хотя бы один из элементов (5) и (6):

1 сл. – работают оба,

2 сл. – работает (5) и не работает (6),

3 сл. – не работает (5) и работает (6).

Тогда событие А: .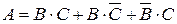

Все три варианта наступления события А несовместны,

а в каждом случае работы блоков 5 и 6 события являются независимыми.

Соответственно, его вероятность

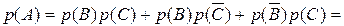
Учитывая, что элемент 5 содержит последовательное соединение 1 и 4 элементов, вероятность его работы равна произведению вероятностей безотказной работы каждого из этих элементов: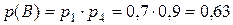

Тогда, .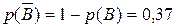

Для нахождения вероятности события С рассмотрим противоположное ему событие 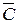- событие, состоящее в том, что элемент (6) не работает. Элемент 6 состоит из параллельно соединённых 2 и 3 элементов, тогда он не работает, когда не работают оба элемента 2 и 3:

;

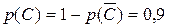
Таким образом, для вероятности события А получим:

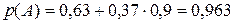Ответ: вероятность безотказной работы схемы равна 0,963.

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒