Непосредственное нахождение вероятности событий —

Если производится некоторый опыт, имеющий 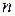 равновозможных исходов, из которых  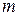исходов благоприятствуют наступлению события А, то вероятность события А, обозначаемая  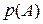или просто 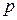, равна отношению числа благоприятствующих исходов к общему числу исходов опыта:

.

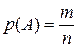1.1. В соревнованиях по толканию ядра участвуют 4 спортсмена из Эстонии, 6 спортсменов из Латвии, 3 спортсмена из Литвы и 7 — из Польши. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Литвы.

Решение. В соревнованиях участвуют 4 + 6 + 3 + 7 = 20 спортсменов. Следовательно, общее число мест для выступлений 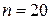. Три из них предназначены спортсменам из Литвы, т. е. т = 3. Т.к. порядок выступлений определяется жребием, то вероятность литовским спортсменам занять любое место из них, в том числе и последнее, одинакова и равна .

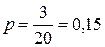1.2.Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 2, но не дойдя до отметки 5 часов.

Решение. Благоприятствующими для наступления нужного события будут 3 деления из 12. Тогда .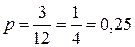

1.3.Покупая карточку лотереи «Спортлото», игрок должен зачеркнуть 6 из 49 возможных чисел от 1 до 49. Если при розыгрыше тиража лотереи он угадает все 6 чисел, то имеет шанс выиграть значительную сумму денег. Чему равна вероятность угадать все 6 номеров?

Решение. Так как число исходов данного опыта конечно, и все они равновозможны, используем классическую формулу вычисления вероятности: .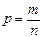

Общее число исходов опыта n равно числу способов выбрать 6 чисел из 49, при этом порядок выбора значения не имеет, значит, считаем число сочетаний из 49 по 6:

.

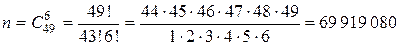К сожалению, благоприятный вариант только один.

Тогда .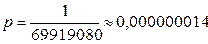

1.4. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу.

Решение. При одном бросании монеты практически возможны два исхода: выпадение герба, орла (О) или цифры, решки (Р). Т.к. монета симметрична, то вероятности этих вариантов одинаковы. При двух бросаниях монеты возможны 4 ( 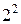) исхода: ОО, ОР, РО, РР. При трёх бросаниях монеты возможны 8 ( 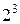) исходов: ООО, ООР, ОРО, РОО, ОРР, РОР, РРО, РРР.