f/. Dãy có chiều dài hữu hạn

f/. Dã y có chiề u dà i hữ u hạ n

Dã y đ ư ợ c xá c đ ị nh vớ i số mẫ u N hữ u hạ n (N đ iể m trê n trụ c hoà nh) gọ i là dã y có chiề u dà i hữ u hạ n. N đ ư ợ c gọ i là chiề u dà i củ a dã y, kí hiệ u là:

L[x(n) ] = N

Ví dụ: L[rect_N(n) ]=N

g/. Nă ng lư ợ ng và cô ng xuấ t củ a dã y.

· Nă ng lư ợ ng củ a mộ t dã y đ ư ợ c đ ị nh nghĩ a như sau:

Trong đ ó 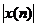là modul củ a x(n).

Ví dụ:

· Cô ng xuấ t trung bì nh củ a dã y:

· Nă ng lư ợ ng củ a dã y x(n) trong khoả ng :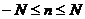

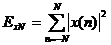
Vậ y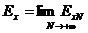

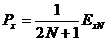
· Dã y nă ng lư ợ ng: nế u nă ng lư ợ ng củ a dã y x(n) là hữ u hạ n thì x(n) đ ư ợ c gọ i là dã y nă ng lư ợ ng.

· Dã y cô ng xuấ t: nế u cô ng xuấ t trung bì nh củ a x(n) là hữ u hạ n thì x(n) đ ư ợ c gọ i là dã y cô ng xuấ t.

3. Cá c phé p toá n cơ bả n củ a dã y

Cho 2 dã y x₁ = {x₁(n)} và x₂ = {x₂(n)} cá c phé p toá n cơ bả n trê n hai dã y đ ư ợ c đ ị nh nghĩ a như sau:

1/. Phé p nhâ n 2 dã y: y = x₁. x₂ = {x₁(n). x₂(n)} (1. 8)

2/. Phé p nhâ n 1 dã y vớ i 1 hệ số: y = a. x₁ = {a. x₁(n)} (1. 9)

3/. Phé p cộ ng 2 dã y: y = x₁ + x₂ = {x₁(n) + x₂(n)} (1. 10)

4/. Phé p dị ch mộ t dã y (Shifting sequence):

- Dị ch phả i: Gọ i y là dã y kế t quả trong phé p dị ch phả i n₀ mẫ u mộ t dã y x ta có:

y(n) = x(n-n₀), vớ i n₀ > 0 (1. 11)

- Dị ch trá i: Gọ i z là dã y kế t quả trong phé p dị ch trá i n0 mẫ u dã y x ta có:

z(n) = x(n+n₀), vớ i n₀ > 0 (1. 12)

Phé p dị ch phả i cò n gọ i là phé p là m trễ (delay). Phé p là m trễ mộ t mẫ u thư ờ ng đ ư ợ c ký hiệ u bằ ng chữ D hoặ c Z^-1. Cá c phé p dị ch trá i và dị ch phả i đ ư ợ c minh họ a trong cá c hì nh 1. 4.

Hì nh 1. 4: (a) Dã y x(n)

(b) Phé p dị ch phaỉ 4 mẫ u tr ê n tí n hiệ u x(n)

Nhậ n xé t: Ta thấ y, mộ t tí n hiệ u x(n) bấ t kỳ có thể biể u diễ n bở i tí n hiệ u xung đ ơ n vị như sau:

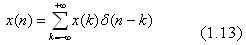
Cá ch biể u diễ n nà y sẽ dẫ n đ ế n mộ t kế t quả quan trọ ng trong phầ n sau.

Ghi chú:

Cá c phé p tí nh thự c hiệ n trê n cá c tí n hiệ u rờ i rạ c chỉ có ý nghĩ a khi tầ n số lấ y mẫ u củ a cá c tí n hiệ u nà y bằ ng nhau.

II. HỆ THỐ NG RỜ I RẠ C

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒