(I-A)^(-1) =I + A+ A^2+A^3+.

X = (I-A)^(-1) Y

Х> =0 кезінде Y> =0. яғ ни теріс емес салалық шығ аруды анық ау есебі шешілді.

Сондық тан, егер Леонтьев моделі ө ндімді болса, онда соң ғ ы сұ раныстың У> =0 кез –келген векторы ү шін жалпы шығ арудың Х> =0 теріс емес векторы анық талады. Бұ л жағ дайда қ атардағ ы келесі ыдырау кері матрицағ а (I-A)^(-1) шығ арылады

(I-A)^(-1) =I + A+ A^2+A^3+...

Сондық тан шығ ару векторын келесі тү рдк интерпретациялауғ а болатын келесі формула бойынша табуғ а болады

X=Y + AY + A^2 Y + A^3 Y+ …,

Берілген Y соң ғ ы сұ раныс кө лемінде ө німдерді ө ндіру ү шін AY қ олданылады, бірақ алдымен оларды жү ргізу керек, A(AY)=A^2 Y не ү шін қ ажет екен. Леонтьев моделінің бұ л кері матрицасын А = (I-A)^(-1) > 0 толық шығ ын матрицасы деп атайды. Оның ә рбір а элементі j –ші соң ғ ы ө нім бірлігін ө ндіру ү шін і –ші қ анша ө нім бірлігі ө ндірілуі тиіс екенін кө рсетеді.

Сол шарттар кезінде ө німдік модель, екі жақ ты модель кірісті болып табылады. Бұ л тең салалық бағ асы қ ұ рылымына қ осылғ ан қ ұ нның ө згеруіне ә серін талдау ү шін Леонтьев моделін қ олдануғ а мү мкіндік береді. Екі жақ ты жү йе матрицасы сияқ ты транспонирленген А^т матрицасы бар, онда қ осылғ ан қ ұ нның ө зегруімен тең бағ алардың ө згеру байланысын анық тауғ а болады. Леонтьевтің статистикалық моделі тек материалдық ғ ана емес, сонымен қ атар ең бек ресурстарын да қ арастыруғ а мү мкіндік береді. Онда берілген А технологиясы кезінде жә не берілген шектелген L ең бек ресурстары кезінде сызық тық перограммалау есебінде соң ғ ы сұ раныс кө лемін максимизациялау туындайды.

Екі жақ ты есептің интерпретациясы р материалдық ресурстарының екі жақ ты бағ алары мен w ең бегінің екі жақ ты бағ асының арасындағ ы аналогияғ а сү йенеді. Егер L- жұ мыс басты саны болса, ондаw –ең бек ақ ы ставкасы. Сондық тан w – салалық шығ ару бірлігіне қ атысты ең бек ақ ығ а кеткен шғ ын векторы, aлp(I —А) бұ рынғ ысынша вектор-қ осылғ ан қ ұ ндар қ атары. Ө німнің оптимальді бағ асы ең бек ақ ы ставкасына тең коэффициентпен толық ең бек шығ ынына пропорционал екенін білдіретін тең дік алынады.

Екіжақ тылық тың бірінші теоремасында тү зудің мақ саттық функциясы мен екі жақ ты есеп оптимум нү ктесінде беттеседі; бұ л тең дік қ ұ ндылық формада экономикалық тепе –тең дік кезінде қ осымша (соң ғ ы ө німнің жалпы қ ұ ны) жә не сұ раныс тең дігін (ең бек ақ ының жалпы қ оры) ө рнектейді. Бұ л жерде ең бек ақ ы ставкасы соң ғ ы ассортименттік жиынтығ ының оның ең бек сиымдылығ ына қ атынасына тең болады. фон Нейман моделі кө псалалы эконимиканың дамуының кең ейтілген моделі болып табылады. Сондық тан фон Нейман моделі бір ө німді ө ндіруді ә ртү рлі тә сілдермен жібереді, оны кең ейтілген Леонтьев моделі ретінде қ арастыруғ а болады. Модклде n ө німдер жә не m ө ндіру тә сілдері кө рсетілген. Ә рбір j-ші тә сіл а шығ ындар бағ аны –векторымен жә не в шығ арулар векторы –бағ анымен беріледі.

Фон Нейман моделі экономиканы, t ағ ымды ө ндірістік циклінде ө німдерді ө ндіру ү шін алдың ғ ы t-1 ө ндірістік циклінде ө ндірілген ө німдер ыдырайды деген ойда тұ йық деп; ол ү шін алғ ашқ ы запастар векторы берілген деп ұ йғ арылады. АХ < =ВХ жү йесі – бұ л табиғ и тү рдегі фон Нейман моделі.

Берілген тү рдегі Фон Нейман моделі жинақ тауды жә не ө ндірістік емес тұ тынуды сипаттамайды.

Екі жақ ты жү йеге келесі тү рде трактацияланатын жү йе аталады:

Р А> = р В,

фон Нейманның тұ йық моделінің бірде бір процессі оң кірісті ә келмейді. Бұ л кезде шығ ындар (t -1 ) –шы жылы жасалынғ ан, ал нә тиже t жылы пайда болатын байқ ауғ а болады. Егер тең дік орындалса, қ ожайын (t -1 )-шы жылда К қ орын салып жә не оны t –шы жылы алса, табиғ и тү рде пайда алады.

Осынлайша басқ а да актуальді ә леуметтік –экономикалық есептер қ арастырылуы мү мкін: запастарды ұ йымдастыру процессін моделдей, ресурстарды тарату жү йесін моделдеу жә не т. б. барлық моделдер кездейсоқ шамалармен, айнымалылармен, параметрлермен сипатталады. Ә леуметтік –экономикалық жү йесін функциялау процессінің моделдеуші алгоритмі блок –схема тү рінде ұ сынылады. Моделдерді программалық реализациялау ә ртү рлі кіріс деректерімен басқ арудың нұ сқ аларын имитациялауғ а жә не кө бірек қ абылдануы бойынша айнымалыларды моделдеуге мү мкіндік береді: біртекті, қ алыпты, экспоненциальді, сызық ты, гамма –таралу сұ раныстары ү шін; Пуассон таралуы, геометриялық жә не биномдық таралу –қ ызметін орындау ү шін. Компьютерлік моделдей нә тижелерін жү йенің барлық функциялау кү йінің сандық сипаттамалары орындайды.

13 лекция. Экологиядағ а компьютерлік моделдеу. Картография есебі.

Ө ндірістік кә сіпорындар тастағ ан кө здермен Тараз қ аласы промзонасының табиғ и ортасының ластануының жағ дайлық моделі қ арастырылады. Адамның шаруашылық ә рекетінен ауа ортасы зиянды заттармен ластанады. Ауа ә ртү рлі газдармен ластанады, олардың ішінде кең тарағ аны кө міртегі тотығ ы, кү кіртті андигрид (қ ос тотық ты кү кірт) жә не азот қ ышқ ылы, мысалы, кө мірсутектер, металл қ ышқ ылы (ртут) жә не органикалық жә не органикалық емес пайда болғ ан ә ртү рлі шаң дар. Ауада ө лшенген шаң ның (аэрозоль) кү йі қ оршау тенденциясына ие. Бірақ ауаның қ атты ағ ымы, жел оны қ айта ө лшенген кү йге келтіруге барады: былайша айтқ анда, қ айта қ алқ ып шығ уы пайда болады. Булар конденсациялану қ асиетіне ие, олар ауадан жауады жә не жоғ арғ ы жақ та отырады.

Сондық тан, жоң ғ ы жылдарда жалғ асып жатқ ан ө ндірістің тө мендеулері, ө ндірістік мекемелерде жасалынғ ан жә не ауағ а сә йкесінше тү сетін ластану кө лемінің тө мендеуі, су объектілері жә не тіректері техногендік жү ктемелердің адекваттық тө мендеуін қ оршағ ан ортағ а аудара салмайды. Сол себептен актуальдік есебі болып біріккен кө здердің ә ртү рлі типтері ү шін есептеудің универсалдық ә дісін қ ұ ру болып табылады.

Тараз қ аласы промзонасының ә уе бассаейнінің негізгі ластану кө здері болып фосфорлық ө ндірістік мекемелер жә не басқ а да ірі мекемелер –ТОО «Казфосфат» жамбылдағ ы филиалы, АҚ " Химпром-2030" , АҚ «Минералдық тың айтқ ыштар», РК-4 жә не Гипстік зауыд болып табылады. Атмосфераның ластануына жасалынғ ан есептеулері негізінде 3D Studio Max ү ш ө лшемді графикасын қ олдану арқ ылы интегралданғ ан Delphi 6. 0 ортасындағ ы ү ш ө лшемді кең істікте программалық ө німді реализациялауды қ арастырамыз. Нә тижелер атмосфера ластануының концентрациясын талдау ү шін ө ндірісте ендірілген болуы мү мкін. Атмосфераның зиянды заттармен ластануын есептеуді жү зеге асыру ү шін ә ртү рлі сандық ә дістер қ олданылады. Атмосфераның ластануын есептеуді жү зеге асыратын сандық ә дістердің бірі Эйлер ә дісі болып табылады. Математикалық модель келесі тү рде қ ұ рылады. Промзона территориясын атмосфераның тө менгі қ абатының барлық мү мкін болғ ан і ластану кө зері бар Ф жиынымен кө рсетейік. Ә рбір j_iÎ Ф кө здері параметрлер векторымен сипатталады, мысалы, геометриялық биіктігі, ә ртү рлі лақ тырылғ ан заттардың массасы, центр координатасы жә не т. б. Ф –ке критерилік бағ алайтын функция Е(j) –ті енгіземіз. Критерилік бағ алаушы Е(j_i) функциясы қ арастырылып жатқ ан аумақ тағ ы атмосфераның тө менгі қ абатының ластану дең гейін сипаттайды.

" Есептеу нә тижелері" менюінде атмосфераның ластануын есептеу іске асырылады. Есептеу нә тижелері Эйлер ә дісін қ олдану арқ ылы ү ш ө лшемді кең істікте суреттеледі (4 сурет). Бұ л терезеде есептеуге қ ажетті барлық параметрлер енгізіледі, сонан соң " Есептеу" тү ймешесін басу кезінде, нә тижелерді шығ ару формасы туралы хабарлама шығ ады. Пайдаланушыда нә тижелерді шығ арудың келесі формаларын таң дау туындайды: 3D-графика, 2D- графика жә не кесте тү рінде. 3D-графиканы таң дау кезінде есептеу жү ргізіледі жә не торлар ә дісі арқ ылы келесі нә тижелер шығ арылады (5 сурет).

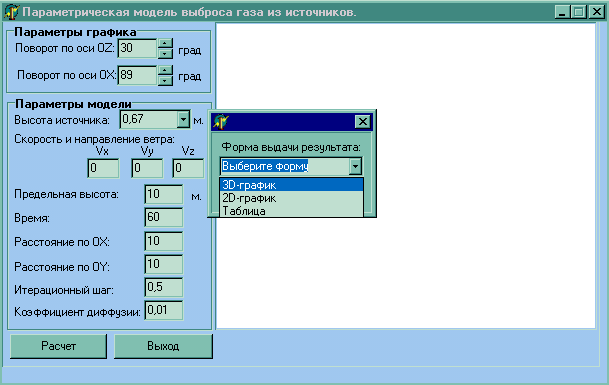
4 сурет – кө здерден газды лақ тырудың параметрлік моделі

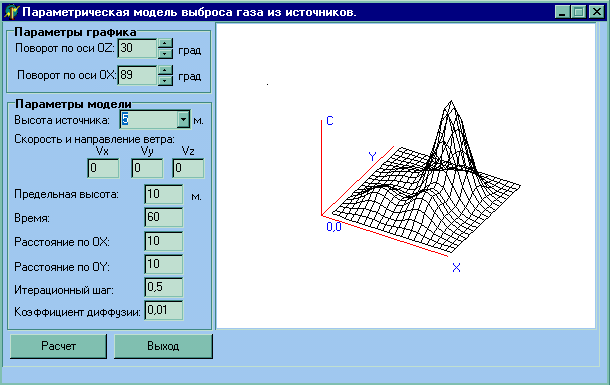
5 сурет – Экологиялық зонаның ү стің гі беті

Тараз қ аласының ө неркә сіптік ө ндірісінің бастапқ ы берілгендері бойынша концентрациясын есептейміз жә не 6-суретте промзонаның зиянды заттарының ә серін қ осатын картасы кө рсетілген

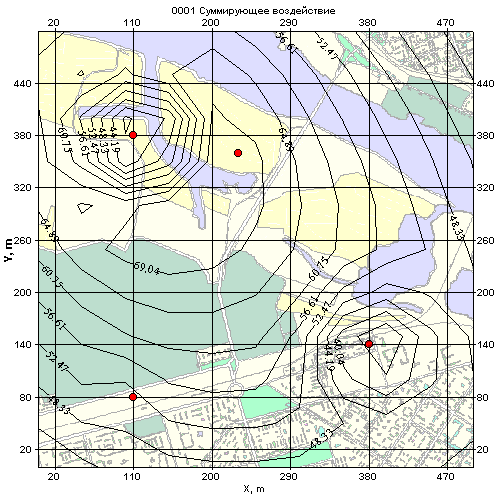
6 сурет - промзонаның зиянды заттарының Карта рассеивания

⇐ Предыдущая 3 4 5 6 7 8 9 101112 Следующая ⇒