9 лекция. Массалық қызмет ету жүйесін моделдеу

Кө птеген кү рделі жү йелерді зерттеу кезінде массалық қ ызмет етуге байланысты есептерді шешу қ ажеттілігі туындайды. Бірақ та массалық қ ызмет ету теориясының аналитикалық аппараты тә жірибелік қ ызығ ушылық ты ұ сынатын барлық есептерді шешуге мү мкіндік бермейді, кіріс ағ ымы қ арапайым ағ ыммен аппроксимацияланатын негізгі есеппен ғ ана шектеледі, ал қ ызмет ету уақ ыты кө рсетілген заң бойынша таралынғ ан деп ұ йғ арылады. Массалық қ ызмет ету жү йесі (МҚ Ж) схемасында келтірілген кү рделі жү йелерді зерттеу ү шін компьютерлік моделдеу қ олданылады.

Бұ рын айтылғ ан моделдеу ә дісі кө мегімен кездейсоқ заң дылық тар берілген сұ раныс ағ ымын реализациялаумен тү рленеді. Ә рі қ арай қ ызмет етуші жү йені функциялау процессі моделденеді. Зерттеушіні қ ызық тыратын жү йе жұ мысының барлық кө рсеткіштері фиксирленеді (фиксируются). Жалпы моделдеуші алгоритм бұ рын берілген кейбір шарттар кезінде жү йені функциялау процессінде кездейсоқ реализациялауды ө ндіреді. Осы кезде жинақ талғ ан ақ параттар статистикалық ө ң деледі.

Қ арапайым ағ ымдар жағ дайындағ ы кү тімі бар жә не қ ызмет етудің кө рсетілген уақ ытындағ ы жү йе ө зімен бірге Марков кездейсоқ процессін ұ сынады.

P_k(t) ық тималдылығ ын қ анағ аттандыратын тең деулерді табамыз. Ә рбір t ү шін мынағ ан тең

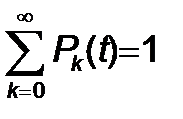. (2)

Алдымен t+h мезетінде барлық приборлар бос болғ анда ық тималдылық ты табамыз. Бұ л келесі тә сілмен орындалады:

- t уақ ытында барлық приборлар бос болды жә не h уақ ытында жаң а талаптар тү скен жоқ;

- t уақ ытында талаптарғ а қ ызмет етумен бір прибор бос емес болды, қ алғ ан басқ а приборлардың бә рі бос болады; h уақ ытында талаптарғ а қ ызмет ету аяқ талады жә не жаң а талаптар тү спейді.

Қ алғ ан мү мкіндіктер: екі немесе ү ш приборлар бос емес болды жә не h уақ ытында оларғ а жұ мыс істеу аяқ талды - o(h) ық тималдылығ ы бар.

Кө рсетілген оқ иғ адағ ы бірінші ық тималдылық мынағ ан тең

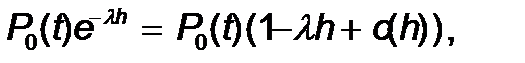
Екінші оқ иғ аның ық тималдылығ ы

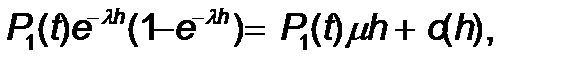
Олай болса,

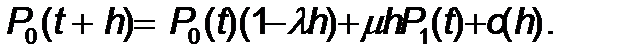
Бұ дан келесі тең деуді аламыз

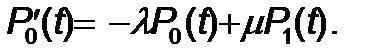(3)

Енді k ³ 1 кезінде P_k(t) ү шін қ ұ рылғ ан тең деуге келеміз. Ә ртү рлі екі жағ дайды бө лек қ арастырамыз: 1 £ k < m жә не k ³ m. Алғ ашында 1 £ k < m болсын делік. t+h уақ ытында E_k кү йіне ө туге болатын маң ызды кү йлерді ғ ана санаймыз. Бұ л мынадай кү йлер:

T мезгілінде жү йе E_kкү йінде болды, h уақ ытында жаң а талаптар тү спеді жә не бір де бір прибор қ ызмет етуді аяқ тағ ан жоқ. Бұ л оқ иғ аның ық тималдылығ ы мынағ ан тең

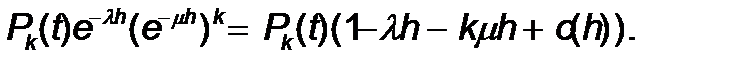
T мезгілінде жү йе E_k-1 кү йінде болды, h уақ ытында жаң а талаптар тү сті, бірақ алдың ғ ы талаптардың бірде бірі қ ыземт етуді аяқ тамағ ан. Бұ л оқ иғ аның ық тималдылығ ы тең

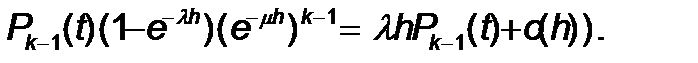
T мезгілінде жү йе E_k+1кү йінде болады, h уақ ытында жаң а талаптар тү скен жоқ, бірақ бір талап етуге қ ызмет кө рсетілді. Бұ ның ық тималдылығ ы тең болады

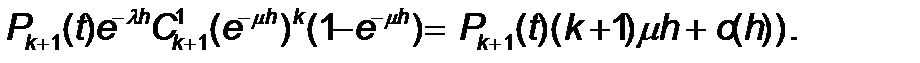
E_k кү йіне ө тудегі барлық қ алғ ан ойлық мү мкіндіктер h уақ ыт аралығ ында ық тималдылық қ а ие, ол 0(h) тең.

Табылғ ан ық тималдылық тарды жинақ тай отырып кедесі тең дікті аламыз:

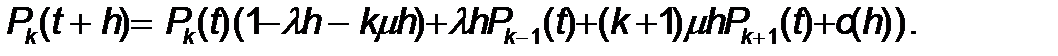
1 £ k < m ү шін кү рделі емес тү рлендірулер бізді келесі тең деуге алып келеді:

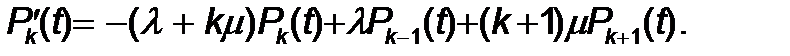(4)

k ³ m ү шін дұ рыс пікірлер келесі тең деуге ә келеді

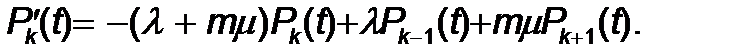(5)

P_k(t) ық тималдылығ ын анық тау ү шін біз (2)-(5) дифференциалдық тең деудің шексіз жү йесін алдық. Оны шешу техникалық қ иындылық ты кө рсетеді.

Массалық қ ызмет ету жү йесінде стационарлық

шешімді анық тау

Массалық қ ызмет ету теориясында ә детте t ®¥ ү шін орнатылғ ан шешім оқ ытылады. Бұ ндай шешімнің бар болуы эргодикалық теоремамен орнатылады, олардың кейбірі бізде кейін орнатылады. Қ арастырылып жатқ ан есепте шектік немесе стационарлық ық тималдылық тар бар. Олар ү шін P_k белгіленуін енгіземіз. t®¥ кезінде 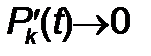болатынын байқ аймыз.

Стационарлық ық тималдылық тар ү шін (3), (4) жә не (5) тең деулері келесі тү рге кө шеді:

(6)

1 £ k < m кезінде

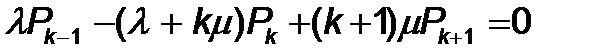(7)

k ³ m кезінде

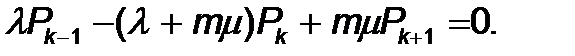(8)

Бұ л тең деулерге нормалайтын шарт қ осылады

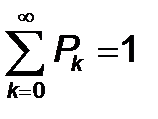(9)

Алынғ ан шексіз алгебралық жү йені шешу ү шін белгілеулер енгіземіз: 1£ k< m кезінде

k ³ m кезінде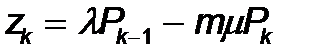

Бұ л белгілеулерде (6)-(8) тең деулер жү йесі мынадай тү рді қ абылдайды:

z₁=0, z_k-z_k+1=0; k ³ 1 кезінде

осыдан аяқ талады, барлық k ³ 1 ү шін z_k =0

яғ ни, 1 £ k < m кезінде

kmP_k=lP_k-1(10)

жә не k ³ m кезінде

mmP_k=lP_k-1 (11)

жазуғ а қ олайлы болу ү шін белгілеу енгіземіз

r=l/m.

(10) тең деу аяқ тауғ а мү мкіндік береді, 1 £ k < m кезінде

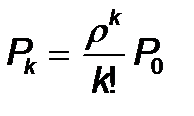(12)

k ³ m кезінде (11) тең деуден мынаны табамыз

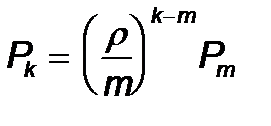
жә не сонымен бірге, k ³ m кезінде

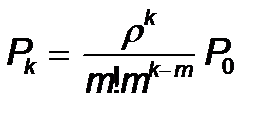(13)

P₀ табу ғ ана қ алады. Ол ү шін (9) тең деуге (12) жә не (13) формулаларынан P_k ө рнегін қ оямыз. Нә тижесінде

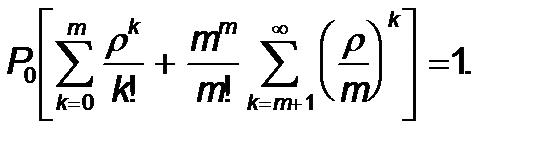
Сонымен квадрат жақ шадағ ы шексіз қ осынды (сумма) тек келесі шарт бойынша табылады

r< m (14)

Онда бұ л жағ дайда келесі тең дік табылады

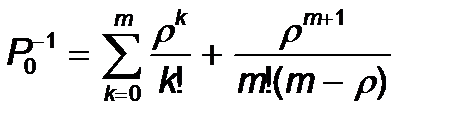(15)

Егер (14) шарт орындалмаса, яғ ни, егер r³ m болса, онда P₀анық тау ү шін кыадрат жақ шаның ішінде тұ рғ ан тең деу ажырап кетеді, демек, P₀ міндетті тү рде 0-ге тең болу керек. бірақ бұ л ү шін (12) жә не (13) –тен барлық k ³ 1 ү шін P_k =0 болады.

Кейбір дайындық нә тижелері.

Кіріспе туралы біз айтып ө ттік. Кү тім ұ зақ тығ ы ө зімен бірге g ә ріпімен белгіленетін кездейсоқ шаманы ұ сынады. Қ азір біз тек қ ызмет ету процессінде орнатылып қ ойғ ан кү тімнің ық тималдылық ұ зақ тығ ының таралуын анық тайтын есепті ғ ана қ арастырамыз. Кү тім ұ зақ тығ ы t ө тетін P{g> t} ық тималдылығ ы арқ ылы белгілейміз, жә не жақ шада кө рсетілген P_k{g> t} тең сіздік ық тималдылығ ы арқ ылы белгілейміз. Толық ық тималдылық формуласы мына тең деумен берілген

P{g> t}= 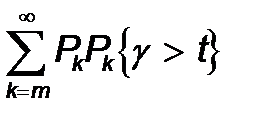(16)

Бұ л формуланы пайдаланушы ү шін қ олайлы тү рге тү рлендірместен бұ рын кейінгі кейбір мә ліметтер ү шін бізге қ ажеттілерді дайындап алайық. Алдымен m=1 жә не m=2 жағ дайлары ү шін P₀ү шін қ арапайым формуланы табамыз. Кү рделі емес тү рлендіру мынадай тең дікпен жү ргізіледі:

m=1 кезінде

P₀=1-r, (17)

m=2 кезінде

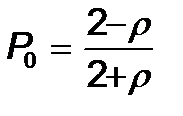(18)

Енді ық тималдылық ты есептейміз. Шамасы, бұ л ық тималдылық мынағ ан тең

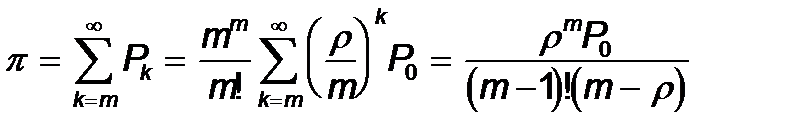(19)

Бұ л формула m=1 ү шін ерекше қ арапайым тү рге ие:

p=r, (20)

m=2 кезінде

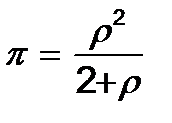(21)

(19) формуладағ ы r мә ні 0- ден m дейінгі кез –келген мә нді қ абылдай алатындығ ан ескертеміз. Сондық тан (20) формуласында r< 1, ал (21) формулада r< 2.

10 лекция. Массалық қ ызмет кө рсету жү йесінде ұ зақ тосуды тарату функциясын анық тау.

Егер талаптар тү су мезгілінде кезекте k-m талаптары бар болса, онда қ ызмет ету кезектік ретпен жү ргізіледі, қ айта тү скен талаптар k-m+1 талабына қ ызмет кө рсетілгенге дейін кү туге міндетті. q_s(t) ық тималдылық ты білдірсін делік. k ³ m тең дік орнына ие

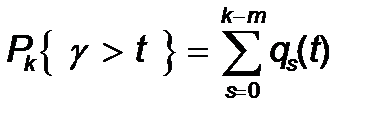
Сонымен қ ызмет ету ұ зақ тығ ының таралуы кезекте қ анша талаптар болуынан, басқ а талаптарда қ ызмет ету ұ зақ тығ ының ұ лылығ ынан кө рсеткіштік жә не тә уелсіз деп ұ йғ арылса, онда t уақ ытындағ ы ық тималдылық бірде бір қ ызмет етулерді аяқ тамайды. Ол мынағ ан тең

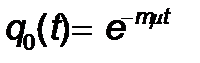
Егер барлық приборлар қ ызмет етуден бос емес болса жә не қ ызмет етуді кү тетін талаптардың жеткілікті кезектері бар болса, онда қ ызмет кө рсетілген талаптар қ арапайым болады. Шынында да, бұ л жағ дайда барлық ү ш шарт –стационарлық, ә рекетке қ атыспау жә не ординарлылық –орындалатын болады. Вероятность освобождения за промежуток времени t уақ ыт аралығ ындағ ы босатылу ық тималдылығ ы тең дей s приборларғ а тең (бұ ны қ арапайым есептеумен кө рсетуге болады)

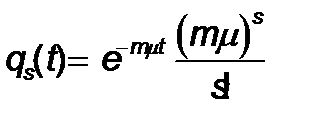
Сонымен,

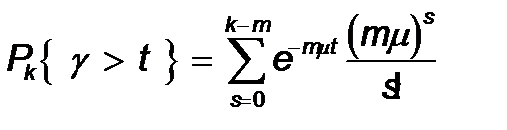
Жә не сонымен қ атар,

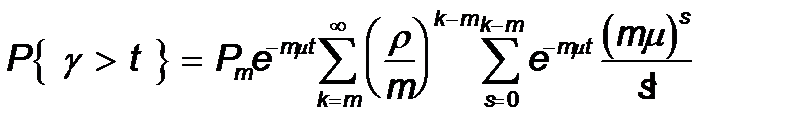
Бірақ P_kық тималдылығ ы белгілі:

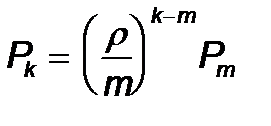
сондық тан

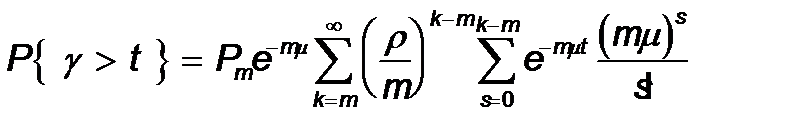
Тү рлендіру арқ ылы соң ғ ы тең деудің оң жақ бө лігін мына тү рдегі тең деуге ә келеміз

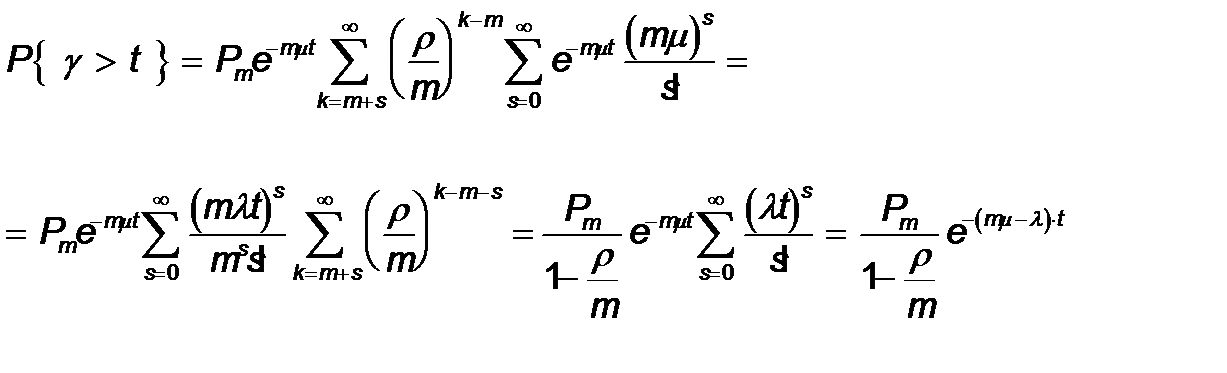
(13) жә не (19) формулаларынан 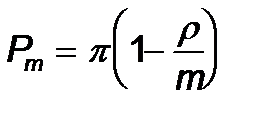тең екенін табамыз, сондық тан t> 0 кезінде

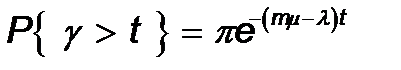(22)

ә рине t< 0 кезінде 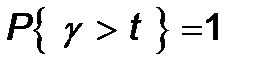болады.

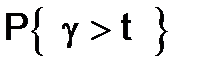функциясы t=0 нү ктесінде ү здіксіз ү зілуі бар.

Кү тімнің орташа ұ зақ тығ ы.

(22) формуласы кү тім ұ зақ тығ ының бізді қ ызық тыратын барлық сандық сипаттамаларын табуғ а мү мкіндік береді. Кү иімнің орташа ұ зақ тығ ы мынағ ан тең

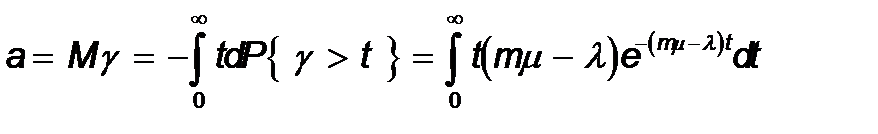
Кү рделі емес есептеулер келесі формулағ а ә келеді

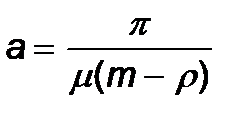(23)

g шамасының дисперсиясы мынағ ан тең болады

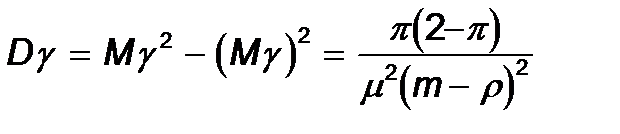(23) формуласы бір талаптағ ы кү тімнің орташа ұ зақ тығ ын береді. Т уақ ыт аралығ ында қ ызмет ету жү йесінде талаптармен уақ ыттың орташа жоғ алуын табамыз. T уақ ытында жү йеде lT орташа талаппен тү седі; жалпы жоғ ару мынағ ан тең

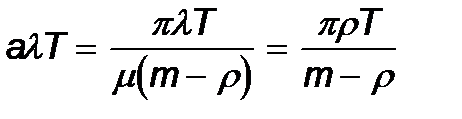(24)

r шамасының ө згеруімен кү тімдегі жоғ алу уақ ыттың суммасының жылдам ө сетінін бізге демаонстрациялйтын ү лкен емес арифметикалық есептеулер жү ргіземіз. Ол ү шін біз T=1 жағ дайымен шектелеміз жә не ең кіші m мә нін қ арастырамыз: m=1 жә не m=2.

m=1 кезінде (20) кү шінде

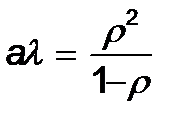
r=0. 1; 0. 3; 0. 5; 0. 9 кезінде; al мә нішамамен 0. 011; 0. 267; 0. 500; 1. 633; 8. 100 тең.

m=2 кезінде (21) -де

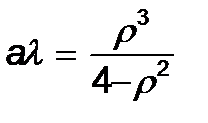
r=0. 1; 1. 0; 1. 5; 1. 9 кезіндеal мә ні шамамен 0. 0003; 0. 333; 1. 350; 17. 587 тең болады.

Келтірілген деректер қ ызмет ету жү йесінің ү лкен сезімталдылығ ына қ атысты белгілі фактіні жақ сы иллюстрациялайды. Ол кезде тұ тынушы кү тім ұ зақ тығ ының мә ндік ө суін дереу байқ айды. Бұ л фактіні массалық қ ызмет ету жү йесінде жабдық тау жү ктемелерін есептеу кезінде міндетті тү рде ескеру керек.

Қ ызмет етудің бір каналдық жү йесі ү шін қ ұ рылғ ан моделдеуші алгоритмдер, сенімді элементтері бар жү йелер.

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒