1 кесте. Кейбір материалдар үшін жылу өткізгіш коэффициенттерінің мәндері

⇐ ПредыдущаяСтр 10 из 12Следующая ⇒

1 кесте. Кейбір материалдар ү шін жылу ө ткізгіш коэффициенттерінің мә ндері

Мыс Алюминий Сталь

Мұ з (0°С) Бетон Кірпіш

2, 23 0, 7-0, 2 0, 7

Асбест Ағ аш Ауа

0, 4-0, 8 0, 1-0, 2 0, 034

Имеем, ограничиваясь первым порядком приращения Dх,

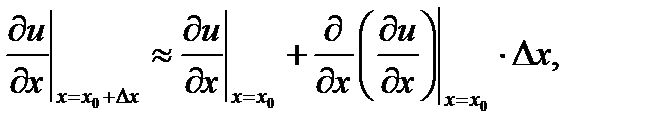кү шінде

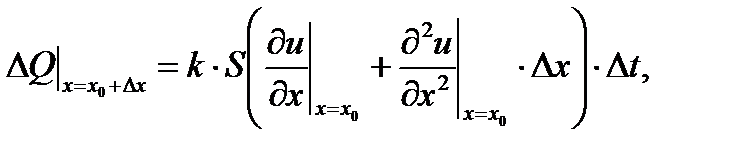
Егер х = х₀ жә не х = х₀+Dх қ йылысулары арқ ылы Dt уақ ытында жылудың ә ртү рлі саны ө ткен болса, онда қ ыздыруғ а ө ткен оның сол бө лігі (немесе, салқ ындаудағ ы таң бадан тә уелді) бар

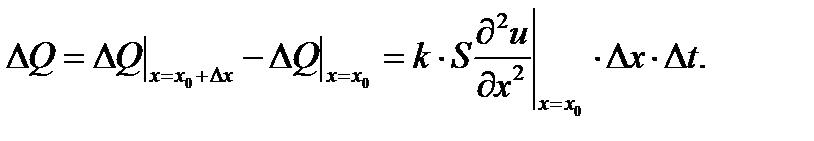
Сол уақ ытта бө лік температурасы Dике ө згерді делік; бұ л DQ = тсDиқ атынасымен DQ ө згеруімен байланысты екені белгілі, мұ ндағ ыт - масса, с - удельная жылусиымдылығ ы. DQү шң н екі ө рнекті тең естіреміз:

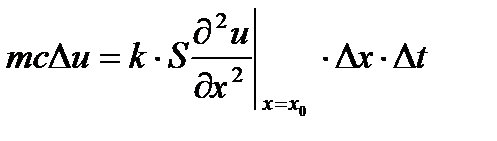Сондық тан массаны т = r * S * Dx ұ сынуғ а болады: (r - зат тығ ыздығ ы), тең деудің екі жағ ын да Dtбө ле отырып жә не Dt® 0 кезінде шегіне ө те отырып, келесіні аламыз

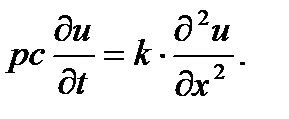
Бұ л –біртекті стержн ү шін негізгі жылу ө ткізгіштік тең деуі. Шығ ару процедурасында бұ л тең деу локальді, яғ ни сол уақ ыт мезетінде жә не сол нү ктеде энергиянық сақ талу заң ын ө рнектейді.

Тең деуге затты сипаттайтын ү ш тұ рақ ты кіреді. Тең деуді келесі тү рде жазу арқ ылы оларды біріктіруге болады

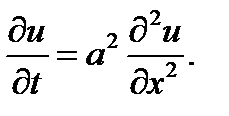(33)

мұ ндағ ы 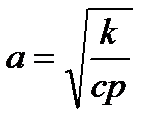-температура ө ткізгіштік коэффициенті. (33)- тегі а²коэффициентінің таң басы -ә рақ ашан оң болады.

(33) тең деуі - ең қ арапайым дифференциалдық тең деулердің бірі. Оның қ арапайымдылғ ына қ арамастан, қ арапайым жағ дайдың ө зінде ондай тең деуді шешуде де кү рделі есептер болады.

Ә леуметтік – экономикалық процесстерді моделдеу

Кө псалалы экономиканың статистикалық сызық тық моделін американың экономисті шығ у тегі орыс В. В. Леонтьев ө ң деп шығ арғ ан болатын (Леонтьев моделі " шығ ын - шығ ару" ). Бұ л модель ө ндірістің техникалық мү мкіндігі туралы деректер негнізінде берілген соң ғ ы сұ раныс бойынша салалардың жалпы шығ аруын анық тауғ а мү мкіндік береді. Моделдер негізіне келесі болжамдар жатады:

1) Экономикалық жү йеде ө ндіріледі, сатылады, сатып алынады жә не n ө німдер инвестицияланады;

2) Экономика салалардан тұ рады, олардың ә рқ айсысы тек бір- ақ ө нім ө ндіреді, ә ртү рлі салалар ә ртү рлі ө нісмдер ө ндіреді, бірлесіп ө ндірілген ә ртү рлі ө німдер шығ арылады;

3) саланың ө ндірістік процессі арқ ылы шығ арылып жатқ ан ө німдегі кейбір (мү мкін барлық ) ө німдерді тү рлендірулер тү сіндіріледі, ол ү шін сол ө німді шығ ару ү шін шығ арылып жатқ ан ө німді болғ ызбайды (мысалы, электроэнергияны ө ндіру кезінде электроэнергияны қ олдану);

4) жұ мсалғ ан ө німдерге қ атысты шығ арылатынғ а тұ рақ ты деп ұ йғ арылады.

Бір жылда і- ші ө німнің жалпы шығ арылуы X екі бө лікке дырайды: барлық салада ө ндірістік тұ тынуғ а жә не соң ғ ы тұ тынуғ а (ө ндірістік емес). Егер ә рбір ө німнің таза шығ аруын жә не оғ ан деген соң ғ ы сұ ранысты тең естіретін болсақ, онда тең деулер жү йесі Леонтьев моделін ұ сынатын тү рге тү рленеді

Х - а Х = У, i=1, 2, …, n

Егер Y_t шамасы экзагендік берілген ретінде қ арастырылса, онда берілген Y кезінде моделдердің n (i = 1, 2, ..., n) сызық тық тең деулері Х салалық шығ аруларын анық тауғ а мү мкіндік береді.

Сондық тан, ә діс маң ыздылығ ы жаратылғ ан коэффициенттер кө мегімен ө рнектелген технологиялық мү мкіндіктер туралы экзогендік берілген соң ғ ы сұ раныстар бойынша салалардың жылпы шығ арылуларын анық таумен аяқ талады. _.. Ә рине, осы тең деу бойынша кері есепті де шешуге болады – берілген жалпы шығ арулар ү шін ә рбір ө німдегі соң ғ ы сұ раныс кө лемін анық тауғ а болады.

X, Y шамалары табиғ и немесе бағ алық ө лшем бірлікте болуы мү мкін; бұ лармен сә йкесінше табиғ и жә не бағ алық салааралық баланс ажыратлады.

Тең деулер жү йесі экономиканың салалық қ ұ рылымын сипаттайды, сондық тан тікелей шығ ынның теріс емес коэффициенттері кезінде жә не Ү соң ғ ы сұ раныс кө лемі кезінде ол міндетті тү рде теріс емес кө лемде X > = 0 (i = 1, 2, ..., п) саласын шығ аруда шешулуі керек. Бұ л жағ дайда жү йе ө ндімдік деп аталады. Қ осрланғ ан жү йе деп сала ө німін бағ алауғ а арналғ ан сызық тық тең деулер жү йесі аталады:

р - а*р = v,

мұ ндағ ы v> =0 - к- шы саланың шығ аруын бірлікке қ осылғ ан қ ұ н. Сондық тан а*р - к-шы саланы бірлік шығ аруының кідіру суммасы, онда екі жақ ты жү йенің сол жақ бө лігінде к –шы саланың бірлік шығ аруынан таза кірісі тұ рады, олар қ ұ нын қ осқ анда тең еседі.

Екі жақ ты жү йе кірісті деп аталады, егер ол теріс емес р, > =0 (i=1, 2, ..., n) шешілетін болса. Ө німділіктен кірістік жә не керісінше шығ атынын кө рсетуге болады, яғ ни бұ л тү сініктер эквивалентті.

Қ ысқ аша векторлық –матрицалық жазбада ө ннімділік жү йесі келесі тү рге ие болады

(I-А) Х = У,

мұ ндағ ы А- тікелей шығ ындар коэффициентінің матрицасы; I- бірлік nxnматрица; Х = (Х,, Х₂,..., Х_П); ¥ = (¥,, ¥,,..., ¥ „); ө німділік шарты екі шартқ а эквивалентті – матрицаның кері шартына жә не кері матрица (I-А) матрицағ а теріс элементтердің болу талаптарына екендігі формуладан белгілі. Бұ л жағ дайда вектор

⇐ Предыдущая 3 4 5 6 7 8 91011 12 Следующая ⇒