37. Лаплас түрлендіруін қолданып, интегралдық және жиіліктік сипатттамаларды қолданып өтпелі үдерістің сапасын анықтау

Интегралдық ө діс негізінде ө шпелі процесс қ исығ ы мен реттелетін шаманың берілген мө ні арасындағ ы ауданды зерттеу қ ағ идасы жатады (9. 4-сурет). Себебі бұ л аудан реттеуге кететін шығ ынды жанама сипаттайды.

Бұ л қ ағ ида бойынша: реттелетін шаманын, берілген мә ні мен ө тпелі процесс қ исығ ы арасындағ ы аудан неғ ұ рлым кішкентай болса, соғ ұ рлым реттеу сапасы жоғ ары. Кө бінесе келесі тү рдегі интегралдық бағ алау кең тарағ ан:

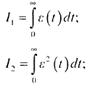
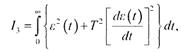
мұ ндағ ы. ε (/) - реттелетін шаманың берілген мә нінен ауытқ уы (реттеу қ ателігі); Т - осы жү йе ү шін ө тпелі процесті ө згертуге мү мкіндік туғ ызатын қ айсыбір экспоненттің уақ ыт тұ рақ тысы. Кө рсетілген интегралдарды минималдау арқ ылы реттеу сапасының ең жоғ ары кө рсеткіштерін қ амтамасыз ететін параметрлердің мә ндерін (АРЖ дифференциалдық тең деуінің коэффициенттерін) табуғ а болады

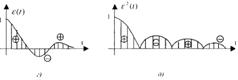
(9. 11) интеграл реттелетін шаманың берілген мә німен ө тпелі процесс қ исығ ының арасындағ ы аудандардың алгебралық (яғ ни, таң баларын ескере отыра) қ осындысын анық тайды. Сол себептен ол тербелмелі емес һ (t) бірсарынды процестерді (9. 4, а, б, в, г-сурет) бағ алау ү шін қ олданылады. Тербелмелі ө тпелі процестің (9. 4, д-сурет) сапасын (9. 12) жә не (9. 13) интегралдары бойынша бағ алағ ан дү рыс

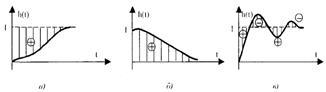Жиіліктік ә діс. Бү л ә діс Фурье тү рлендіруіне жә не тү йық АРЖ ө тпелі процесі мен комплексті жиіліктік сипаттама арасындағ ы бірмә нді байланыстың болуына негізделген. Сонымен, жиіліктік сипаттамалар бойынша ө тпелі процесс сапасын бағ алауғ а болады.

АРЖ зерттеудің жиіліктік ә дісінде жү йені қ обалжыту ә сері ретінде сатылы сигнал қ олданылады:

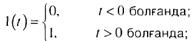
Бү л функцияны ү зіліссіз гармоникалық қ атарғ а тҮ зу Дирихле интегралы кө мегімен іске асырылады:

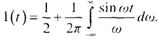
Егер АРЖ комплекстік жиіліктік сипаттамасы 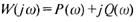болса, онда жү йенің берілген қ обалжыту сигналынан туатын ө тпелі процесін мына формулалар бойынша есептеуге болады:

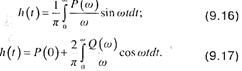
Алынғ ан (9. 16) жә не (9. 17) ө рнектері, бірлік сатылы сигнал ә серінен туатын ө тпелі процесс сапасын жиіліктік ә діспен зерттеудің негізінде жатады; бү лардың кез - келгенін пайдалана отыра, реттеу сапасы жө нінде алғ ашқ ы жуық татылғ ан қ ағ иданы қ ү руғ а болады:

⇐ Предыдущая 21 22 23 24 25 262728 29 30 Следующая ⇒