30. Рауса критериі. 31. Лаплас түрлендіруін автоматтық реттеу теориясында қолдану

30. Рауса критериі

1877 ж. Раус реттеу жү йесінің орнық тылық шартын анық тады, ол тұ рақ ты коэффициенттерден тұ ратын сызық ты кез-келген қ атарлы дифференциалдық тең деулермен сипатталады.

Раус критериясы дә лелсіз тӛ мендегідей анық талады. С0 оң коэффициентпен n дә режелі тең деу берілген деп қ арастырайық, онда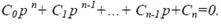

Алдығ а қ ойылғ ан мақ сатқ а жету ү шін n+1 қ атарлы Раус кестесі қ ұ рылады.

(7. 4)

Кестенің бірінші тӛ менгі бӛ лігі тақ санды коэффициенттер тең деуімен, ал екінші қ атары жұ п санды коэффициенттер тең деуімен қ ұ рылады.

Жоғ арғ ы қ атарлы коэффициенттер тӛ менгі екі қ атарлы коэффициенттер арқ ылы тӛ мендегі шартпен кӛ рсетіледі. Тӛ менгі бірінші екі қ атардан бастап бір қ атармен жоғ ары кӛ теріп матрица қ ұ рады

Бірінші қ атарды қ осатын алдың ғ ы ә рбір минорлар келесі матрицаның жоғ арғ ы қ атарының ізделген коэффициенттерін тізбектей қ ұ рады.

Орнық тылық шарты барлық матрицалардың бірінші қ атарындағ ы бӛ ліктердің оң болуы, яғ ни С0 > 0; С1 > 0; b0 > 0; b1 > 0; а0 > 0.

Бұ л шарттың бұ зылу саны сипаттамалық тең деудің тү бір санына тең, ол оң комплекстік жазық тық та орналасқ ан.

31. Лаплас тү рлендіруін автоматтық реттеу теориясында қ олдану

Динамикалық жү йелердің сызық ты дифференциал тең деулері Лаплас тү рлендіруіне негізделген операторлық ә діспен шешіледі.

Лаплас тү рлендіруі нақ ты уақ ыттық айнымалы функцияны f(t) комплекстік айнымалы функцияғ а F(p) тү рлендіреді:

Кейбір функциялардың бейнелері:

1) Бірлік функция:

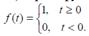
Бірлік функцияның бейнесі:

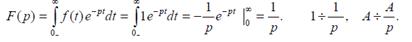
2) Кө рсеткіш функцияның бейнесі:

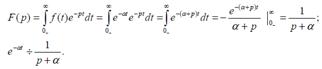
3) Синус функцияның бейнесі: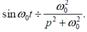

4) Косинус функцияның бейнесі: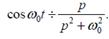

Беріліс функциясы – бұ л бастапқ ы мә ндер нө лге тең болатын шарттар кезінде шығ ыс шаманың Лаплас бойынша бейнесін кіріс шаманың Лаплас бойынша бейнесіне қ атынасы

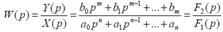
Автоматты басқ ару жү йесінде екі полиномдардың бұ л қ атынасы операторлық беріліс функциясы деген атқ а ие. Динамикалық тү рде жү йенің қ асиетін сипаттайтын беріліс функцияның бө лімі сипаттамалық полином деп аталады. Тең деудің тү бірлерін жү йенің полюсі деп аталады. Жү йенің шығ ыс шамасының бейнесін алу ү шін кіріс шаманың бейнесін беріліс функцияғ а 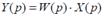кө бейтсек жеткілікті.

Лаплас бейнесі бойынша жү йенің беріліс функциясы келесі қ асиеттерге ие: 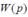коэффициенттері ә рқ ашан да нақ ты (заттық ) жә не алымының полином дә режесі бө лімінің полином дә режесінен аз болады.

Дифференциалды тең деулерді Лаплас тү рлендіруін қ олданып шешу келесідей болады:

а) берілген кіріс ә сері 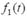бойынша Лаплас тү рлендіруі кө мегімен 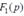бейнесін табамыз;

б) дифференциалды тең деу бойынша беріліс функцияны 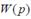қ ұ райды;

в) шығ ыс шаманың бейнесін 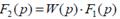бойынша анық тайды;

г) Белгілі шығ ыс шаманың бейнесі бойынша шығ ыс функцияның тү пнұ сқ асын табамыз

Шығ ыс функцияның тү пнұ сқ асын табу ү шін тү пнұ сқ а кестесін не болмаса жіктеу теоремасын пайдаланады

⇐ Предыдущая 16 17 18 19 202122 23 24 25 Следующая ⇒