32. Автоматты басқару жүйелерінің теңдеулері және жиіліктік сипаттамалары

Автоматты басқ ару жү йелерді қ ү ру ү шін зерттелетін объектілерді алгебралық жә не дифференциал тең деулермен ө рнектеу қ ажет. Тең деулердің статика не орнық қ ан режим тең деулері жә не динамика не ө тпелі процесс тең деулері тә різді екі тү рі бар. Статика тең деулері жоспарланган ә сердің тү рақ ты болуына қ арай, ә детте алгебралық болып табылады, ал динамика тең деулері ә детте дифференциалды. Олар ауытқ ыту кү шінің ә серінен туатын ө тпелі процесс кезіндегі, не олар аяқ талғ аннан кейінгі жү йенің қ алпын айқ ындайды. Динамика тең деуін жасау ү шін автоматты жҮ йе жеке буындарғ а ажыратылып, олардың ә рқ айсысы Ү шін сол буында ө тетін процеске тә н физикалық заң негізіне сә йкес тең деулер қ ү рылады. Автоматты жҮ йенің барлық элементтері ү шін қ ү рылғ ан динамика тең деулерінің жиынтығ ы автоматты басқ ару процесін анық тайды.

х_кірарқ ылы элементар буынның кірісіне ық пал ететін физикалық шаманы, ал х_шығаркылы сол буынның шығ ыстық параметрін белгілесек(4. 1-сурет), онда буынның дифференциал тең деуі жалпы тү рде мынандай болады:

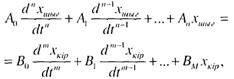
мұ ндағ ы п – х_шығө згерісі ө рнектелетін дифференциг| тең деудің реті; " t”- уақ ыт.

Динамикалық буындардың маң ызды сипаттамасы жиіліктік беріліс функциясы болып табылады. Оларды қ арсы ә сер нө лге тең болғ анда, гармоникалық ә серді кіріске бере отыра жү йенің орнық ты режимін қ арастыру кезінде аламыз.

Кірісте гармоникалық ә сер болғ ан кездегі 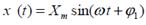динамикалық буынды қ арастыралық.

Комплексті тү рде: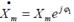

мұ ндағ ы X m -амплитуда;

 1  - бастапқ ы фаза;

  - осы ә сердің бұ рыштық жиілігі.

Орнық ты режимде сызық ты буынның шығ ысында сол жиіліктің гармоникалық функциясы болады, бірақ жалпы жағ дайда   бұ рышқ а кіріс фазамен салыстырғ анда фаза бойынша ығ ысқ ан болады.

Шығ ыс шама: 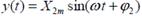. Комплексті тү рде: 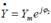Стандартты тү рде сызық ты буынның дифференциалды тең деуі келесі тү рде ө рнектеледі:

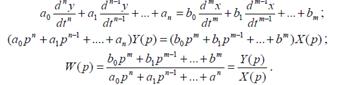
Комплекстік жиілікті сипаттаманы p   j    ауыстырып алғ анда қ арастырылады.

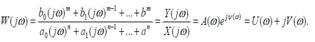(5. 4)

Шығ ыс функцияның комплексті мә ні кіріс функцияның комплексті мә ніне қ атынасы комплексті жиілікті беріліс функция деп аталады:

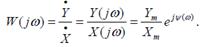(5. 5)

Жиіліктік беріліс функция W( j ) комплекстік сан, модулі шығ ыс функцияның амплитудасының кіріс функцияның амплитудасының қ атынасына тең. Ал аргументі – кіріс қ атынасы бойынша шығ ыс шаманың

фазаларының ығ ысуы:

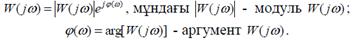Осылайша, жү йе кірісіне гармоникалық сигналы берілсе, шығ ыста орнық тыланғ ан гармоникалық шама кіріс шаманы комплексті жиілік функциясына кө бейтумен анық талады.

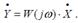
Комплекстік беріліс функцияны келесі тү рде қ арастыруғ а болады:

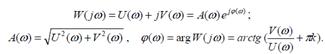
Комплексті жазық тық та жиілікті беріліс функция W( j ) ұ зындығ ы - A( ) тең болатын векторды кө рсетеді, ал аргументі (осы вектормен нақ ты оң полюстен қ ұ ралғ ан бұ рыш) -  ( ). Жиілігі 0 - ден  - дейін ө згеру кезіндегі осы вектордың соң ы комплексті жазық тық та сипаттайтын қ исық ты

амплитудалы-фазалы жиіліктік сипаттама деп атайды. Амплитудалы - фазалы жиіліктік сипаттама W( j )  U( )   jV( ) жиіліктік беріліс функциясына сә йкес болатын векторлардың (годограф) соң ының геометриялық орнын кө рсетеді. Жиілікті нө лден шексіздікке дейін ө згертіп, абсцисса ө сі бойынша нақ ты бө лігін, ал ордината ө сі бойынша жорамал бө лігін бейнелейді. Ә р жиілік ү шін нү кте белгіленеді. Алынғ ан нү ктелерді бір-бірімен қ осады (5 сурет).

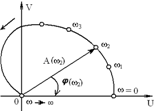
5 сурет – Буынның амплитудалы-фазалы жиіліктік сипаттамасы

⇐ Предыдущая 17 18 19 20 212223 24 25 26 Следующая ⇒