33. Раусс орнықтылық критериі бойынша кесте-сұлбаны құру

33. Раусс орнық тылық критериі бойынша кесте-сұ лбаны қ ұ ру

1877 ж. Раус реттеу жү йесінің орнық тылық шартын анық тады, ол тұ рақ ты коэффициенттерден тұ ратын сызық ты кез-келген қ атарлы дифференциалдық тең деулермен сипатталады.

Раус критериясы дә лелсіз тӛ мендегідей анық талады. С0 оң коэффициентпен n дә режелі тең деу берілген деп қ арастырайық, онда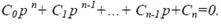

Алдығ а қ ойылғ ан мақ сатқ а жету ү шін n+1 қ атарлы Раус кестесі қ ұ рылады.

(7. 4)

Кестенің бірінші тӛ менгі бӛ лігі тақ санды коэффициенттер тең деуімен, ал екінші қ атары жұ п санды коэффициенттер тең деуімен қ ұ рылады.

Жоғ арғ ы қ атарлы коэффициенттер тӛ менгі екі қ атарлы коэффициенттер арқ ылы тӛ мендегі шартпен кӛ рсетіледі. Тӛ менгі бірінші екі қ атардан бастап бір қ атармен жоғ ары кӛ теріп матрица қ ұ рады

Бірінші қ атарды қ осатын алдың ғ ы ә рбір минорлар келесі матрицаның жоғ арғ ы қ атарының ізделген коэффициенттерін тізбектей қ ұ рады.

Орнық тылық шарты барлық матрицалардың бірінші қ атарындағ ы бӛ ліктердің оң болуы, яғ ни С0 > 0; С1 > 0; b0 > 0; b1 > 0; а0 > 0.

Бұ л шарттың бұ зылу саны сипаттамалық тең деудің тү бір санына тең, ол оң комплекстік жазық тық та орналасқ ан.

Сипаттамалық полином мына тү рде болады:

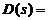
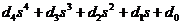
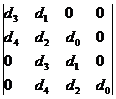
2 кесте - Раус кестесі

№

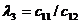
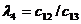
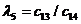
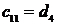
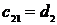
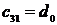
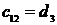
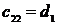
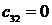
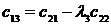
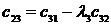
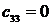
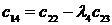
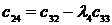
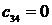
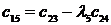
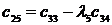
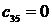
34. Найквист орнық тылық критерийдың интерпретациясы логарифмдік тү рде

Бұ л жиілікті орнық тылық критерийі 1932 жылы америка ғ алымы Г. Найквист ашқ ан. Тұ йық талмағ ан жү йенің АФС тү рі бойынша тұ йық талғ ан жү йенің орнық тылығ ын анық тауғ а мү мкіндік береді.

Демек, тұ йық талмағ ан жү йенің беріліс функциясы тө мендегідей болсын

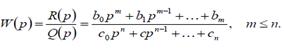
Тең деуге 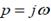қ ойып, тұ йық талмағ ан жү йенің жиіліктік беріліс функциясын табамыз.

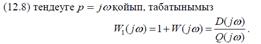Айтылғ анды негізге ала отыра, Найквисттың орнық тылық критерийін қ алыптастыруғ а болады: Егер тұ йық талмағ ан жү йе орнық сыз болса, онда тұ йық талғ ан жү йе орнық ты болу ү шін   бұ рыш жиілігі 0 - ден бастап   дейін ө згерткен кезде тұ йық талмағ ан жү йенің W  j   АФС ( 1, j0) нү ктесін оң бағ ытта l/2 рет қ амтуы тиіс. Мұ ндағ ы l - тұ йық талмағ ан жү йенің сипаттамалық тең деуінің оң тү бірлер саны.

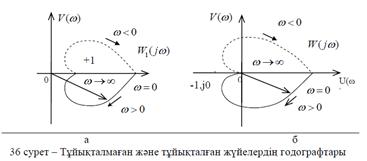
Тұ йық талғ ан жү йелердің орнық тылығ ы ү шін қ ажетті жә не жеткілікті шарты мынандай болады. Тұ йық талғ ан жү йе орнық ты болғ ан жағ дайда W1  j  векторының АФС координат басын қ амтуы қ ажет емес (36а сурет), ал W  j  АФС координат   1, j0  нү ктесін қ амтуы тиіс емес (36 б сурет)

Найквист критерийінің анық тамасын қ алыптастырамыз: егер тұ йық талмағ ан жү йе орнық ты болса, онда тұ йық талғ ан жү йе орнық ты болады, егер тұ йық талмағ ан жү йенің 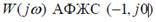нү ктесін қ амтымауы тиіс

⇐ Предыдущая 19 20 21 22 232425 26 27 28 Следующая ⇒