y’’=f(x), y’’=f(x,y’), y’’=f(y,y’) түріндегі дифференциалдық теңдеулерді шешудің әдістері.

3.y’’=f(x), y’’=f(x,y’), y’’=f(y,y’) түріндегі дифференциалдық теңдеулерді шешудің әдістері.

1) Квадратура әдісі. y’=ʃf(x)dx+c₁

y(x)=ʃ(ʃf(x)dx)dx+c₁x+c₂

ʃf(x)dx=φ(x)

2) y’’=f(x,y’), y’=p, y’’=p’алмастыру арқылы

p’=f(x,p)немесе F(x,p,p’)=0 бірінші ретті теңдеуге келтіріледі.

3) Тәуелсіз айнымал айқын түрде кірмейтін F(y,y’,…,y⁽ⁿ⁾)=0 теңдеуі y’=p(y) алмастыру арқылы реті бірге төмендетілген теңдеуге келеді. Бұл алмастыру үшін

y’’==p,

10. Екінші ретті тұрақты коэффицентті, сызықты, біртекті дифференциялдық теңдеулер.

Екінші ретті коэффиценттері тұрақты біртекті жәй сызықтық дифференциялдық теңдеуді қарастырайық:

a₀y’’+a₁y’+a₂y=0 (1)

теңдеуі берілсін дейік, мұндағы а₀, а₁, а₂ коэффиценттері тұрақты сандар.

Бұл теңдеудің дербес шешімін y(x)=e^kx түрінде іздеп көрейік, мұнд. K- анықтауға жататын белгісіз. (1)- теңдеудің сол жағына y(x)=e^kx, y’(x)=e^kx , y’’(x)=e^kx өрнектерін қойып, мына теңдеуді шығарып аламыз.

(a₀k²+a₁k+a₂) e^kx=0.

e^kxфункциясы х-тің ешбір мәнінде нөлге тең болмайтындықтан y(x)=e^kx функциясы (1)-теңдеудің шешімі болуы үшін a₀k²+a₁k+a₂ үшмүшелігі нөлге тең болуы қажетті және жеткілікті. a₀k²+a₁k+a₂ үшмүшелігі характеристикалық үшмүшелік, ал a₀k²+a₁k+a₂=0 теңдеуі(1)-дифференциялдық теңдеудің характеристикалық теңдеуі деп аталады.

Характеристикалық үшмүшелікті қарастырғанда әртүрлі жағдайларға кездесеміз.

1-жағдай. Сипаттамалық үшмүшліктің әртүрлі нақты екі түбірі бар дейік, оларды k₁ және k₂арқылы белгілейік және k₁¹k₂ сонда біз (1)- теңдеудің әртүрлі дербес екі шешімін :

у₁(x)=e^k₁^x және у₂(x)=e^k₂^x

шығарып аламыз. Бұл дербес екі шешім бір-бірімен бірі сызықтық байланыссыз, барлық сан өсінде негіздік дербес шешімдер жүйесін құрып, Вронскийдің анықтауышы деп аталатын екі ретті анықтауышты береді:

w(x)= 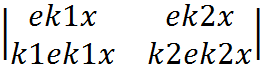=(k₂-k₁)×e^(k1+k2)x¹0.

Демек (1)-теңдеудің жалпы шешімі мына түрде жазылады:

y (x)= C₁×e^k₁^x+C₂× e^k₂^x.

2-жағдай. Енді сипаттамалық үшмүшеліктің бір-біріне тең нақты екі түбірі бар болсын. Бұл жағдайда a₀k²+a₁k+a₂ квадрат үшмүшеліктің дискриминанты нөлге тең. Сондықтан

K₁=k₂=k₀=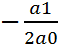

Бұл жағдайда сипаттамалық теңдеудің нақты бір шешімін у₁(x)=e^k₀^x бірден жазып аламыз. Ал, екінші дербес шешімді бірінші дербес шешімнен сызықтық тәуелсіз етіп, у₂(x)=х×e^k₂^x түрінде таңдап аламыз. Сонда сипаттамалық үшмүшелікке сәйкес (1)- теңдеудің жалпы шешімі былай жазылады: y (x)= C₁×e^k₀^x+C₂×х e^k₀^x =(C₁+C₂x) e^k₀^x.

3-жағдай. Егерде сипаттамалық үшмүшеліктің түбірлері комплекс сандар болса, k1=a+ib ; k2=a-ib, онда (1)-теңдеудің жалпы шешімі былай жазылады:

1-Мысал:

1)y’’-5y’+6y=0 теңдеуін алып қарастырайық. Бұл теңдеудің сипаттамалық үшмүшелігінің k₂-5k+6 түбірлері k₁=2; k₂=3. Сондықтан сипаттамалық теңдеудің негіздік дербес шешімдер жүйесі: у₁(x)=e^2x және у₂(x)=e^3x шешімдерінен тұрады. Демек біртекті екінші ретті дифференциялдық теңдеудің жалпы шешімі:

y (x)= C₁×e^2x+C₂× e^3x болады.

2-Мысал.

y’’+6y’+13y=0 дифференциалдық теңдеудің жалпы шешімін табу керек.

Шешуі. Берілген теңдеудің k²-2k+1=0 сипаттаушы теңдеуінің k=-3 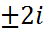түбірлері комплекс түйіндес сандар. Теңдеудің сызықтық тәуелсіз шешімдері y₁=e^-3xcos2x, y₂=e^-3xsin2x фуекциялар болып, оның жалпы шешімі y=e^-3x(C₁cos2x+C₂sin2x) болады.

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒