
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Екі айнымалыға тәуелді курделі функция туындысы
1. Екі айнымалы функция туралы жалпы түсінік:
2. Күрделі екі айнымалы функцияның туындысы:
.
3. Кез-келген бағыт бойынша туынды және градиент.
4. Жоғарғы ретті дербес туындылар және дифференциалдар.
5. Екі айнымалы функцияның экстремумы.
6. Бірінші ретті дифференциалдық теңдеулер. Коши есебі.
7. Бірінші ретті сызықты дифференциалдық теңдеулер
8. Толық дифференциал түріндегі бірінші ретті дифференциалдық теңдеулер
9. Екінші ретті дифференциалдық теңдеулер, Коши теоремасы. Ретін төмендетуге болатын екінші ретті дифференциалдық теңдеулер:
a) .
10. Екінші ретті тұрақты коэффициентті, сызықты, біртекті дифференциалдық теңдеулер. (СБДТ)
11. Сандық қатар және оның жинақтылығы. Қатар жинақтылығының қажеттілік белгісі.
12. Сандық қатаржинақтылығының жеткілікті белгілері.
13. Таңбалары ауыспалы сандық қатарлар:
14. Функциялық қатарлар. Дәрежелік қатарлар:
15. Тейлор мен Маклорен қатарлары:
16. Дәрежелік қатардың практикалық қолдануы
17. Кездейсоқ оқиғалар. Ықтималдықтың анықтамалары.
18. Қайталанбалы тәуелсіз сынақтар. Бернули формуласы.
19. Дискреттік кездейсоқ шамалар. Үлестірім заңдары.
20. Үзіліссіз кездейсоқ шамалар жәнеолардың сандық сипаттамалары:
21. Үзіліссіз кездейсоқ шамалар үшін көрсеткіштік және қалыпты үлестірімдер:
1.Екі айнымалы функция туралы жалпы түсінік:
Функция графигін z=C жазықтығымен қиғанда пайда болатын сызық z=f(x,y) функциясының деңгейлік сызығы деп аталады. f(x,y)=C
Анықтама.Егер белгілі бір ереже немесе заң бойынша М жиынындағы тәуелсіз 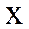 ,
, 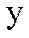 айнымалыларының әрбір қос
айнымалыларының әрбір қос 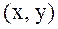 мәніне Z жиынынан алынған z-тің тек қана бір мәні сәйкес келсе, онда z айнымалысы М жиынындағы
мәніне Z жиынынан алынған z-тің тек қана бір мәні сәйкес келсе, онда z айнымалысы М жиынындағы 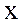 ,
, 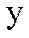 тәуелсіз айнымалыларының функциясы деп аталады да,
тәуелсіз айнымалыларының функциясы деп аталады да, 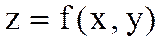 немесе
немесе 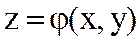 , немесе
, немесе 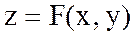 , т.с.с белгіленеді.
, т.с.с белгіленеді.
Нақты сандар 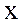 пен
пен 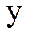 -тің реттелген
-тің реттелген 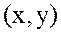 қос мәні декарт жазықтығының А
қос мәні декарт жазықтығының А 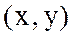 нүктесіне сәйкес келетін болғандықтан, екі айнымалды функцияларды жазықтықтағы нүктенің функциясы түрінде жазуға болады, яғни,
нүктесіне сәйкес келетін болғандықтан, екі айнымалды функцияларды жазықтықтағы нүктенің функциясы түрінде жазуға болады, яғни, 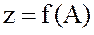 ,
, 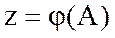 немесе
немесе 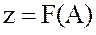 , т.с.с.
, т.с.с.
Жоғарыдағы анықтамада сөз болған М жиыны функцияның анықталу аймағы деп аталады.
Анықталу облыстары көрсетіліп, аналитикалық жолмен немесе формуламен берілген функциялардың бірнеше мысалдарын келтірейік. Мына формула 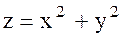 барлық
барлық 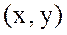 қос мәндері үшін функцияны анықтайды,ал
қос мәндері үшін функцияны анықтайды,ал 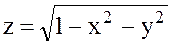 формула тек қана
формула тек қана 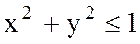 теңсіздігін қанағаттандыратын
теңсіздігін қанағаттандыратын 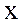 пен
пен 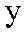 мәндерде функцияны анықтайды. Бұл мысалдардан, екі айнымалды функция үшін айнымалының өзгеру облысы есептің шартына қарай әртүрлі және күрделі болып келетінін көреміз.Осы қарастырылған екі айнымалды функция ұғымын n айнымалды функцияға жалпылауға болады.
мәндерде функцияны анықтайды. Бұл мысалдардан, екі айнымалды функция үшін айнымалының өзгеру облысы есептің шартына қарай әртүрлі және күрделі болып келетінін көреміз.Осы қарастырылған екі айнымалды функция ұғымын n айнымалды функцияға жалпылауға болады.
Дербес туынды.Бізге кеңістіктің Q аймағында анықталған үзіліссіз функциясы берілсін. Осы аймақта жататын нүктесін аламыз. Егер пен -ке тұрақты мен мәндерін беріп -ті өзгертетін болсақ, онда бір айнымалы -тің ( маңайында) функциясы болады. Енді мәніне өсімшесін берсек, онда функцияның
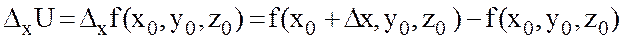
өсімшесін табамыз.Функцияның осы өсімшесі 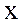 бойынша алынған дербес өсімше деп аталады. Ал мына шек
бойынша алынған дербес өсімше деп аталады. Ал мына шек 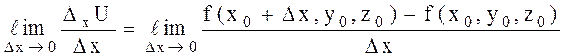
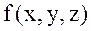 функциясының
функциясының 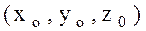 нүктесінде
нүктесінде 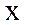 бойынша алынған дербес туынды деп аталады да, келесі символдардың бірімен белгіленеді:
бойынша алынған дербес туынды деп аталады да, келесі символдардың бірімен белгіленеді:
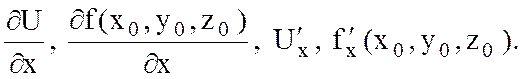
Бұл символдардың төменгі жағында тұрған индекс туындының қай айнымалы бойынша алынатынын көрсетеді. Сондай-ақ, 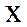 пен
пен 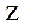 тұрақты, ал
тұрақты, ал 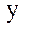 -ті айнымалы деп алып,
-ті айнымалы деп алып, 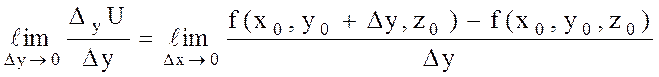
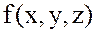 функциясының
функциясының 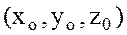 нүктесіндегі
нүктесіндегі 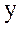 бойынша алынған дербес туындысын анықтаймыз.
бойынша алынған дербес туындысын анықтаймыз.
Берілген 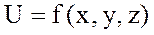 функцияның кез келген бір айнымалысы бойынша нүктедегі дербес туындысы мен сол айнымалының өсімшесінің көбейтіндісі функцияның дербес дифференциалы деп аталады және былай белгіленеді:
функцияның кез келген бір айнымалысы бойынша нүктедегі дербес туындысы мен сол айнымалының өсімшесінің көбейтіндісі функцияның дербес дифференциалы деп аталады және былай белгіленеді: 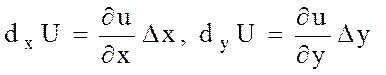
Егер тәуелсіз айнымалы 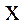 -тің
-тің 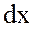 дифференциалын
дифференциалын 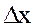 өсімшесі деп алсақ,онда
өсімшесі деп алсақ,онда 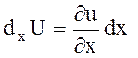 ,сол сияқты
,сол сияқты 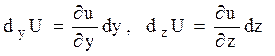 түрінде жазылады.
түрінде жазылады.
Мысал 4. Берілген 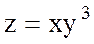 функцияның толық дифференциалын табу керек.
функцияның толық дифференциалын табу керек.
Шешуі: Бұл функцияның дербес туындыларын табайық. 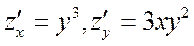 демек,
демек,
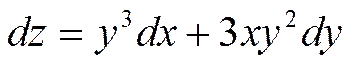
2.Екі айнымалыға тәуелді курделі функция туындысы
Егер z=f(x,y) , x=x(t), y=y(t) болса, онда z=f[x(t);y(t)] болып t-ның күрделі функциясы болады. Сонда
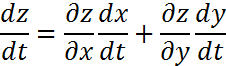
Дербес жағдайда z=(x;y),y=y(x) болса,онда
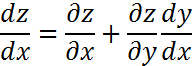
y=y(x)функциясыf(x,y)=0 айқындалмаған түрде берілсе:
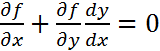 немесе y’=-f’x/f’y
немесе y’=-f’x/f’y
Егер z=f(x,y),мұндағы x=x(u;v), y=y(u;v)болса,онда
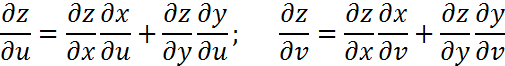
Айнымалдар саны екіден көп болған жағдайда да бұл формулалардың құрамы сақталады.
Мысалы. z=x2+xy+y2,x=t2,y=t3 болса, 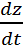 туындыны табу керек
туындыны табу керек
Шешуі: 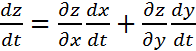 формуласы бойынша толық туынды
формуласы бойынша толық туынды
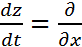 (x2+xy+y2)
(x2+xy+y2) 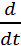 (t2)+
(t2)+ 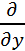 (x2+xy+y2)
(x2+xy+y2) 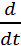 (t3)= =(2x+y)2t+(x+2y)*3t2=(2t2+t3)2t+(t2+2t3)3t2=6t5+5t4+4t3
(t3)= =(2x+y)2t+(x+2y)*3t2=(2t2+t3)2t+(t2+2t3)3t2=6t5+5t4+4t3
Толық дифференциал.Жуықтап есептеу
Егер тәуелсіз айнымалылардың 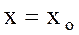 ,
, 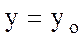 ,
, 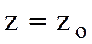 мәніне
мәніне 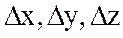 өсімшелерін берсек, онда
өсімшелерін берсек, онда 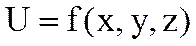 функциясы
функциясы
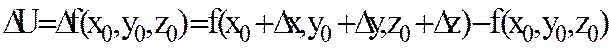 (7.5)
(7.5)
өсімшесін алады. Берілген функцияның осы өсімшесін оның толықөсімшесідеп атайды.
Теорема 1 Егер 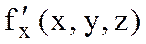 ,
, 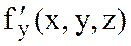 ,
, 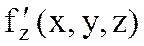 дербес туындылар
дербес туындылар 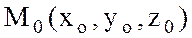 нүктесімен оның қандайда болмасын бір
нүктесімен оның қандайда болмасын бір 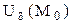 маңайында бар болып және осы нүктеде (
маңайында бар болып және осы нүктеде ( 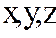 -тің функциясы ретінде) үзіліссіз болса, онда берілген
-тің функциясы ретінде) үзіліссіз болса, онда берілген 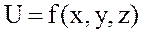 функциясының толық өсімшесі мына түрде жазылады:
функциясының толық өсімшесі мына түрде жазылады:
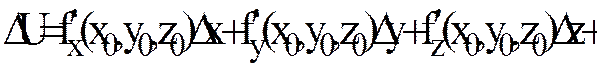
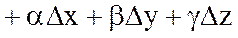 ,
,
мұндағы 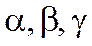 шамалары
шамалары 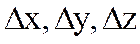 өсімшелеріне тәуелді және
өсімшелеріне тәуелді және 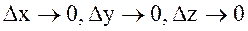 -да
-да 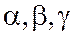 -ларда 0-ге ұмтылатын ақырсыз аз шамалар.
-ларда 0-ге ұмтылатын ақырсыз аз шамалар.
Теорема 2 Егер Q аймағында анықталған 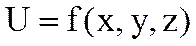 функциясының осы аймақтағы
функциясының осы аймақтағы 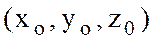 мен
мен 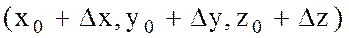 нүктелері үшін толық өсімшесі
нүктелері үшін толық өсімшесі
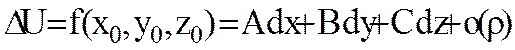 (7.6)
(7.6)
түрінде жазылатын болса (А,В,С-тұрақтылар, 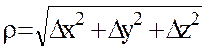 ), онда берілген функцияның
), онда берілген функцияның 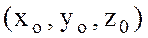 нүктесінде дербес туындылары бар болады.
нүктесінде дербес туындылары бар болады.
Анықтама Егер 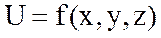 функциясының толық өсімшесі (5) немесе (6) формулаларының бірімен өрнектелетін болса, онда бұл функция
функциясының толық өсімшесі (5) немесе (6) формулаларының бірімен өрнектелетін болса, онда бұл функция 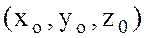 нүктесінде дифференциалданатын функция деп аталады. Сонымен бірге, берілген функцияның толық өсімшесінің сызықты бас бөлімі
нүктесінде дифференциалданатын функция деп аталады. Сонымен бірге, берілген функцияның толық өсімшесінің сызықты бас бөлімі 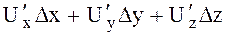 оның толықдифференциалы деп аталады да,
оның толықдифференциалы деп аталады да, 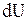 немесе
немесе 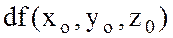 деп белгіленеді.
деп белгіленеді.
Сонымен үзіліссіз дербес туындылары бар кез келген көп айнымалды функция дифференциалданады.
Тәуелсіз 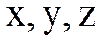 – айнымалыларының өсімшелері олардың дифференциалдары деп алынатынын ескерсек,
– айнымалыларының өсімшелері олардың дифференциалдары деп алынатынын ескерсек, 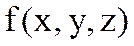 функцияның толық дифференциалы
функцияның толық дифференциалы 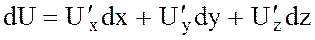 немесе
немесе
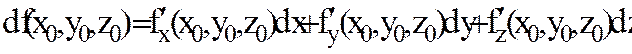
түрінде жазылады. Яғни көп аргументті функцияның толық дифференциалы оның дербес дифференциалдарының қосындысына тең.
Жуықтап есептеу. 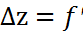 x(x,y)
x(x,y) 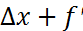 y(x;y
y(x;y 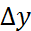 )+○(
)+○( 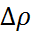 ) және df=dz=f’x(x;y)
) және df=dz=f’x(x;y) 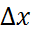 +f’y(x;y)
+f’y(x;y) 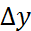 теңдіктерді салыстырғанда,
теңдіктерді салыстырғанда, 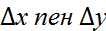 жеткілікті кіші шама болса,функцияның толық өсімшесі мен толық
жеткілікті кіші шама болса,функцияның толық өсімшесі мен толық
дифференциалы арасында жуық теңдік жазуға болады: 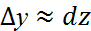 .Немесе
.Немесе
f( 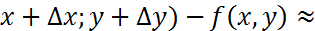 f’x(x,y)
f’x(x,y) 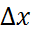 +f’y(x,y)
+f’y(x,y) 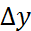
Бұдан f( 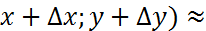 f(x,y)+f’(x,y)
f(x,y)+f’(x,y) 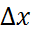 +f’y(x,y)
+f’y(x,y) 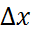
Мысал,(1,04)2,03санды жуықтап есептеу керек.
Шешуі. (1,04)2,03 саны 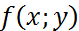 =xyфункциясының x+
=xyфункциясының x+ 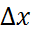 =1,04,y+
=1,04,y+ 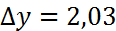 болғандағы дербес мәні х=1,
болғандағы дербес мәні х=1, 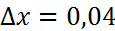 , y=2,
, y=2, 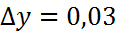 деп алсақ,f(x,y)=f(1;2)=12=1,әрі f’x(x,y)=xylnx, f’x(1,2)=2, f’y(1,2)=0 екенін ескерсек, (1,04)2,03=1+2*0,04+0*0,03=1,08.
деп алсақ,f(x,y)=f(1;2)=12=1,әрі f’x(x,y)=xylnx, f’x(1,2)=2, f’y(1,2)=0 екенін ескерсек, (1,04)2,03=1+2*0,04+0*0,03=1,08.
 3.Берілген бағыт бойынша туынды. Градиент
3.Берілген бағыт бойынша туынды. Градиент
Мысалы.z=x2y+y2функциясының М (1;2) нүктесіндегі ММ1 вектор бағыты, мұндағы М1 (3;0), бойынша туындысын табу керек.
Шешуі ММ1 векторының бағыттаушы косинустарын табамыз:ММ1= {3-1;0-2}={2;-2}=2i-2j;
│MM1│= 2√2/.
ē= 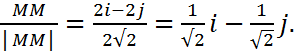
Демек cosα= 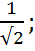 cosβ=
cosβ= 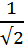 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|