Жоғары ретті дербес туындылар мен дифференциалдар

4.Жоғары ретті дербес туындылар мен дифференциалдар

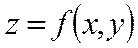екі айнымалының функциясы берілсін. Дербес туындылар 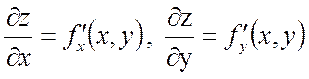жалпы айтқанда х және у айнымалыларының функциясы болады. Сондықтан олардан тағы да дербес туынды табуға болады. Екі айнымалының екінші ретті туындысы төртеу болады. Өйткені 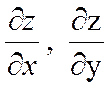функциясының әрқайсысын х және у бойынша дифференциалдаймыз. Оларды былай белгілейміз.

, .

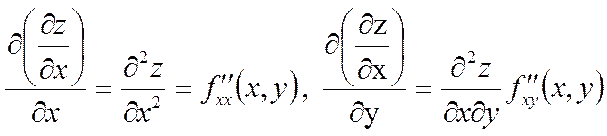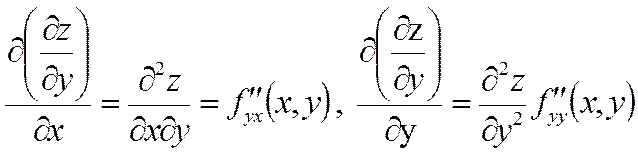Жалпы айтқанда n-ші ретті туынды (n-1)-ші ретті туындыдан алынған бірінші ретті туынды болады. Әртүрлі айнымалысы бойынша алынған екінші ретті немесе жоғарғы дербес туындылар аралас дербес туындылар деп аталады.

Келесі 3-ші, 4-ші тағы сол сияқты ретті туындылар да осылай анықталады. Әр түрлі айнымалылар бойынша алынған жоғары ретті туындыны аралас дербес туынды дейді.

Мысал Берілген 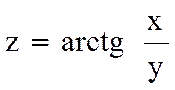функциясының екінші ретті дербес туындыларын табайық.

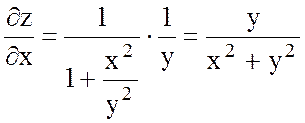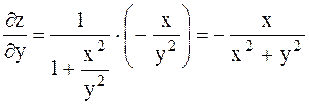
Енді екінші рет дифференциалдаймыз: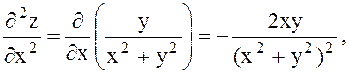

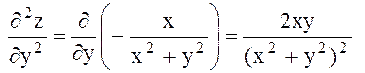
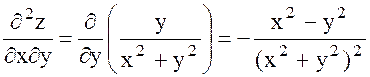Аралас дербес туындылар жөнінде мынадай теорема орындалады.

Теорема 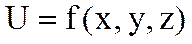функциясы Q облысында анықталып осы облыста 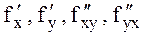туындылары бар болса, және 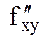пен 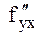туындылары 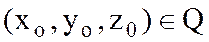нүктесінде үзіліссіз болса, онда 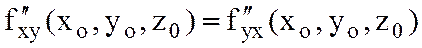теңдігі орындалады.

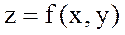функциясының Q облысында бірінші ретті үзіліссіз туындылары болса, онда функцияның толық дифференциалы 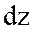деп мына формула бойынша анықталады:

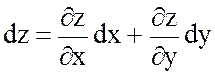мұндағы 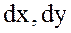- тәуелсіз 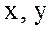айнымалыларының дифференциалдары (ақырсыз аз өсімшелері).

Егер 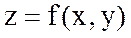функциясының екінші ретті үзіліссіз дербес туындылары бар болса, онда 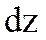-тің бірінші ретті үзіліссіз дербес туындылары бар болады және осы 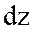дифференциалының толық дифференциалы 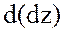берілген 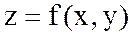функциясының екінші ретті дифференциалы деп аталады. Сонымен, дифференциалдау ережесін пайдаланып төмендегі формулаға келеміз:

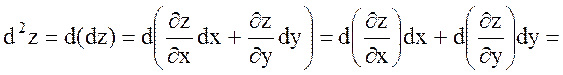
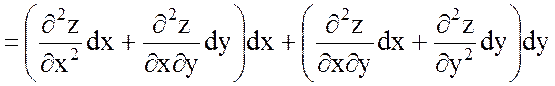
немесе, аралас туындылардың өзара тең болатынын ескеріп,

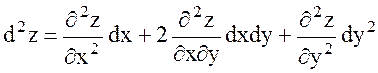
теңдігіне келеміз. Үшінші ретті дифференциал 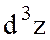-те және одан жоғары ретті басқа дифференциалдар да осы сияқты анықталады. Жалпы функцияның 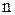-ші ретті дифференциалы

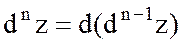теңдігі арқылы анықталады.

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒