
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
А) Қатарларды салыстыру белгісі.
А) Қатарларды салыстыру белгісі.
Мүшелері теріс емес сандар болатын қатарлардың жинақталатынын немесе жинақталмайтынын іс жүзінде бұл қатарды жинақталатыны немесе жинақталмайтыны алдын-ала белгілі басқа бір қатармен салыстыру арқылы дәлелдейді. Салыстыру белгісі сандық қатар жинақталуының жеткілікті белгісі болады.
1-теорема (жинақтылықтың жеткілікті белгісі)
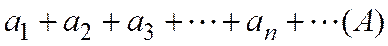 және
және 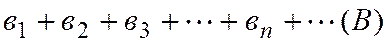
оң таңбалы қатарлары берілген дейік.
Айталық бірінші қатардың мүшелері екінші қатардың сәйкес мүшелерінен артық болмасын:
 (2,1)
(2,1)
Және (В) қатары жинақты болсын. Сонда (А) қатары да жинақты және оның қосындысын (В) қатарының қосындысынан арпайды.
2-теорема. Айталық  (А) және
(А) және 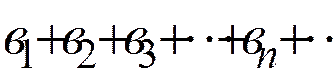 (В) қатарлары берілсін. Сонымен бірге
(В) қатарлары берілсін. Сонымен бірге 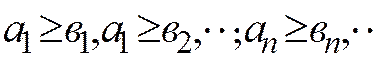 және (В) қатары жинақсыз болсын. Сонда (А) қатары да жинақсыз болады.
және (В) қатары жинақсыз болсын. Сонда (А) қатары да жинақсыз болады.

В) Даламбер белгісі.
Мүшелері теріс емес сандар болатын сан қатарларын, іс жүзінде, жинақталу немесе жинақталмауға зерттегенде Даламбер және Кошидің жеткіліктібергілері аса пайдалы болып табылады. Бұл белгілердің дәлелдеулері, егер салыстырма қатары ретінде әдейі таңдалған сәйкес геометриялық прогрессияны алса, салыстыру белгісінен тікелей шығады.
а) Егер оң таңбалы
 (2,9)
(2,9)
қатарының  мүшесінің
мүшесінің 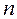 -мүшесіне қатынасы
-мүшесіне қатынасы 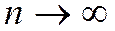 -дағы шегі, яғни
-дағы шегі, яғни  (2,10) шегі бар болса, онда
(2,10) шегі бар болса, онда 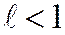 болғанда қатар жинақты, ал
болғанда қатар жинақты, ал 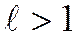 болғанда жинақсыз болады.
болғанда жинақсыз болады.
Дәлелдеу. а) Айталық 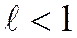 болсын. Қатардың жинақты болатынын көрсетейік. Шынында
болсын. Қатардың жинақты болатынын көрсетейік. Шынында  болғандықтан, шектің анықтамасына сәйкес кез келген
болғандықтан, шектің анықтамасына сәйкес кез келген 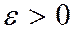 саны үшін
саны үшін 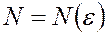 нөмірін
нөмірін 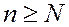 болғанда қатардың барлық мүшелері
болғанда қатардың барлық мүшелері 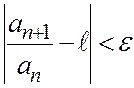 теңсіздігі орындалатындай етіп таңдап алуға болады. Бұдан,
теңсіздігі орындалатындай етіп таңдап алуға болады. Бұдан, 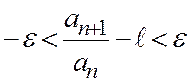
 немесе
немесе 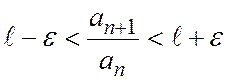 болатынын шығады. Ал
болатынын шығады. Ал 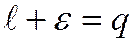 десек,
десек,  теңсіздігін аламыз.
теңсіздігін аламыз.
ә) Айталық 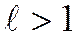 болсын. Қатардың жинақсыз болатынын көрсетейік. Шынында, бұл жағдайда,
болсын. Қатардың жинақсыз болатынын көрсетейік. Шынында, бұл жағдайда, 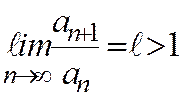 болғандықтан,жеткілікті үлкен
болғандықтан,жеткілікті үлкен  нөмірден
нөмірден  бастап
бастап  немесе
немесе 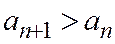 теңсіздігі орындалады. Сонымен,
теңсіздігі орындалады. Сонымен, 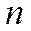 нөмірлі мүшесінен бастап, қатардың мүшелері артады. Сондықтан
нөмірлі мүшесінен бастап, қатардың мүшелері артады. Сондықтан 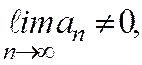 яғни жинақты қажетті шарты бұзылады. Демек, қатар жинақсыз болады екен.
яғни жинақты қажетті шарты бұзылады. Демек, қатар жинақсыз болады екен.
Демек, берілген қатар жинақты.
Даламбер белгісімен қатардың жинақты, не жинақсыз болатынына жауап ала алмаған жағдайда, яғни 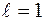 болғанда, салыстыру белгілерінен басқа тағы да бір жеткілікті белгілерді қолдану мүмкін болады. Енді тағы бір жеткілікті белгіні-Кошидің белгісін келтрейік.
болғанда, салыстыру белгілерінен басқа тағы да бір жеткілікті белгілерді қолдану мүмкін болады. Енді тағы бір жеткілікті белгіні-Кошидің белгісін келтрейік. 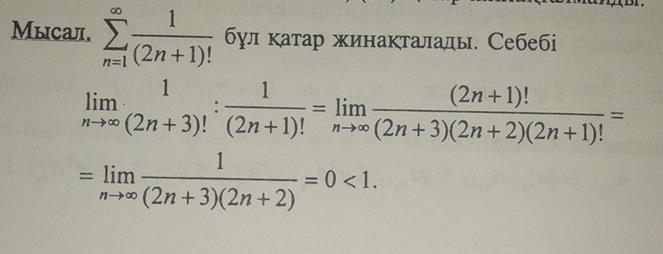
с) Коши белгісі. Егер оңтаңбалы 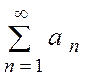 қатары үшн
қатары үшн 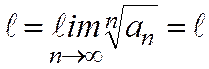 шегі бар болса, онда қатар
шегі бар болса, онда қатар 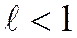 болғанда жинақты, ал
болғанда жинақты, ал 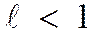 болғанда жинақсыз болады.
болғанда жинақсыз болады.
Кошидың интегралдық белгісі. Айталық
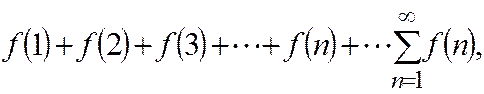 яғни мүшелері
яғни мүшелері 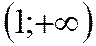 аралығында үздіксіз, оң және кемімелі кейбір
аралығында үздіксіз, оң және кемімелі кейбір 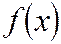 функциясының мәндері болатын қатары берілсін. Сонда
функциясының мәндері болатын қатары берілсін. Сонда
а) егер 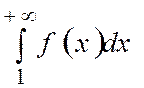 жинақты болса, онда
жинақты болса, онда 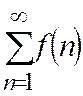 қатары да жинақты болады,
қатары да жинақты болады,
ә) егер 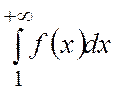 жинақсыз болса, онда
жинақсыз болса, онда 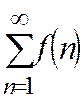 қатары да жинақсыз болады.
қатары да жинақсыз болады.

 13.Ауыспалы таңбалы қатарлар. Лейбинц белгісі
13.Ауыспалы таңбалы қатарлар. Лейбинц белгісі

(Un>0)


 14.Функциялық қатарлар. Дәрежелік қатарлар
14.Функциялық қатарлар. Дәрежелік қатарлар
Айталық қатардың мүшелері х-тен тәуелді болса, онда ол қатарды функциялық қатар дейді, яғни 
Егер 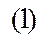 функциялық қатар
функциялық қатар 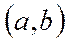 аралығында әрбір х-тің мәнінде жинақты болса онда
аралығында әрбір х-тің мәнінде жинақты болса онда 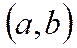 аралығын қатардың жинақтылау облысы дейді. Функциялық қатарлардың ішіндегі толық зерттелгені және тәжірибелік мәселелерде көп кездесетін дәрежелік қатарлар. Дәрежелік қатар деп төмендегі функциялық қатарды айтады.
аралығын қатардың жинақтылау облысы дейді. Функциялық қатарлардың ішіндегі толық зерттелгені және тәжірибелік мәселелерде көп кездесетін дәрежелік қатарлар. Дәрежелік қатар деп төмендегі функциялық қатарды айтады.  . Егер
. Егер 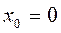 болса, онда бұл қатар мына түрге көшеді.
болса, онда бұл қатар мына түрге көшеді. 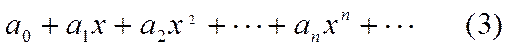 .
.
Егер (3) дәрежелік қатар 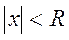 болғанда жинақталатын қатар, ал
болғанда жинақталатын қатар, ал 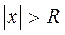 болғанда жинақталмайтын қатар болса, онда
болғанда жинақталмайтын қатар болса, онда 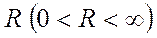 саны дәрежелік қатардың жинақталу радиусы деп аталады.
саны дәрежелік қатардың жинақталу радиусы деп аталады.
Жинақталу радиусын анықтау үшін келесі формулаларды қолданады  және
және 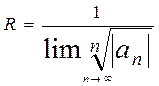 .
.
Мысал.  дәрежелік қатардың жинақталу радиусы анықтау керек .
дәрежелік қатардың жинақталу радиусы анықтау керек .
Шешімі : Мұнда 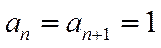 , сондықтан
, сондықтан  . Жинақталу интервалы
. Жинақталу интервалы 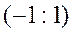 .
.
Абель теоремасы.
Теорема. (Абель теоремасы). Егер дәрежелік қатар х – тің х=х0 м2н3нде жина0талатын 0атар болса онда ол 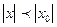 теңсіздігін қанағаттандыратын х – тің барлық мәндерінде абсолютті жинақталады.
теңсіздігін қанағаттандыратын х – тің барлық мәндерінде абсолютті жинақталады.
Теорема. Егер дәрежелік қатар х=х0 мәнінде жинақталмайтын болса, онда ол х – тің 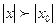 теңсіздігіе қанағаттандыратын барлық мәндерінде де жинақталмайды.
теңсіздігіе қанағаттандыратын барлық мәндерінде де жинақталмайды.
Анықтама. Егер дәрежелік қатар 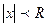 болғанда жинақталатын қатар, ал
болғанда жинақталатын қатар, ал 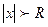 болғанда жинақталмайтын қатар болса, онда R саны дәрежелік қатардың жинақталу радиусы деп аталады.
болғанда жинақталмайтын қатар болса, онда R саны дәрежелік қатардың жинақталу радиусы деп аталады.
Сонымен 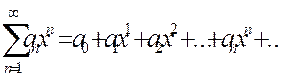 қатардың жинақталу облысы
қатардың жинақталу облысы
(-R,R) интервалы болып табылады, интервал ұштарында қатардың жинақталу немесе жинақталмауы туралы мәселе x=-R және x=R мәндерін қатарға қойғанда шығатын сәйкес сандық қатарларды зерттеу арқылы шешіледі, егер бұл сан қатарлары жинақталатын қатарлар болса, онда олардың жинақталуы абсолютті де немесе абсолютсіз де болуы мүмкін.
Дәрежелік қатардың қасиеттері:
1. (3) қатар кез келген [-r;r], r<R кесіндіде жинақталады.
2. (3) қатардың S(x) қосындысы (-R;R) жинақталу аралығында үзіліссіз және осы аралықта ақырсыз рет дифференциалданады.
3. (3) қатарды кез келген [α,β] тиісті (-R;R) кесіндіде мүшелеп интегралдауға болады.
4. (3) қатарды жинақталу аралығында мүшелеп дифференциалдауға болады.
15. Тейлор және Маклорен қатарлары.
f(x) функциясы а – R<x<a+R аралығында анықталған және кез келген ретті туындылар бар болсын. Тейлор формуласы бойынша
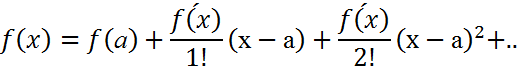
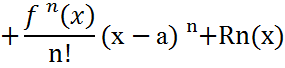
Мұндағы 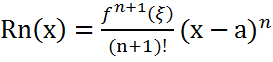 . ξ =a+θ(x-a), 0<θ<1
. ξ =a+θ(x-a), 0<θ<1
Егер n→∞, Rn(x)→0 болса, онда
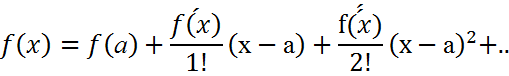
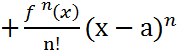 қатары Тейлор қатары деп аталады. Rn(x) – Тейлор қатарының қалдық мүшесі дейді.
қатары Тейлор қатары деп аталады. Rn(x) – Тейлор қатарының қалдық мүшесі дейді.
Егер а 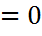 болса, онда Тейлор қатары Маклорен қатары деп аталады да
болса, онда Тейлор қатары Маклорен қатары деп аталады да
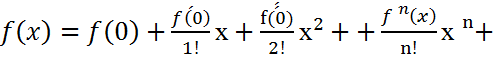 түрінде б/ды
түрінде б/ды
Егер 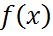 функциясы (а – R; a+R) аралығында анықталып, кез келген n үшін
функциясы (а – R; a+R) аралығында анықталып, кез келген n үшін 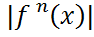 <M теңсіздігі орындалса (мұндағы М-оң тұрақты сан),онда осы функция
<M теңсіздігі орындалса (мұндағы М-оң тұрақты сан),онда осы функция
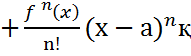 атары Тейлор қатары деп аталады. Rn(x) – Тейлор қатарының қалдық мүшесі дейді.
атары Тейлор қатары деп аталады. Rn(x) – Тейлор қатарының қалдық мүшесі дейді.
Егер а 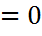 болса, онда Тейлор қатары Маклорен қатары деп аталады да
болса, онда Тейлор қатары Маклорен қатары деп аталады да
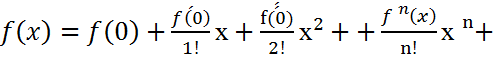 түрінде б/ды
түрінде б/ды
Егер 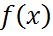 функциясы (а – R; a+R) аралығында анықталып, кез келген n үшін
функциясы (а – R; a+R) аралығында анықталып, кез келген n үшін 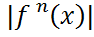 <M теңсіздігі орындалса (мұндағы М-оң тұрақты сан),онда осы функция
<M теңсіздігі орындалса (мұндағы М-оң тұрақты сан),онда осы функция
Тейлор қатарына жіктеледі. Кейбір функциялардың Маклорен қатарына жіктелуі:
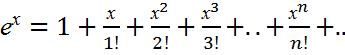 (-∞<x<∞)
(-∞<x<∞)
shx= 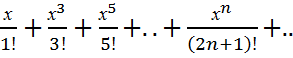 (-∞<x<∞)
(-∞<x<∞)
chx=1+ 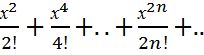 (-∞<x<∞)
(-∞<x<∞)
sinx=  (-∞<x<∞)
(-∞<x<∞)
cosx= 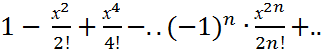 (-∞<x<∞)
(-∞<x<∞)
Жуықтап есептеулерде 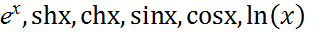 функциялардың Маклорен қатарларына жіктелуін пайдалану керек. Ал логарифмді есептеу үшін
функциялардың Маклорен қатарларына жіктелуін пайдалану керек. Ал логарифмді есептеу үшін
Ln(1+x)=lnx+..+2 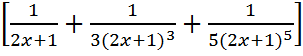 формуласын пайдаланған тиімді
формуласын пайдаланған тиімді
 16.Дәрежелік қатар және олардың қасиеті
16.Дәрежелік қатар және олардың қасиеті
Анықталған интегралдыаналитикалық шешу үшін Ньютон-Лейбниц формуласын қолданады: 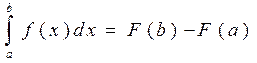 мұндағы
мұндағы 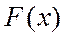 -
- 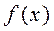 функциясының алғашқы функциясы. Бірақ практикада бұл формуланы екі себепке байланысты қолдана алмаймыз:
функциясының алғашқы функциясы. Бірақ практикада бұл формуланы екі себепке байланысты қолдана алмаймыз:
1) 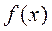 -функциясының алғашқы түрін қарапайым функциялар арқылы сипаттай алмайтындықтан;
-функциясының алғашқы түрін қарапайым функциялар арқылы сипаттай алмайтындықтан;
2) 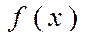 -функциясының шамасы тек кесте түрінде берілсе.
-функциясының шамасы тек кесте түрінде берілсе.
Бұл жағдайларда интегралды шешу үшін сандық әдістер қолданады. Сандық әдіс бойынша анықталған и нтегралдың мәні 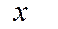 осімен,
осімен,  және
және  түзулерімен және
түзулерімен және 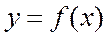 функциясының қисығымен шектелген трапецияның ауданына тең.
функциясының қисығымен шектелген трапецияның ауданына тең.
Трапецияның ауданың есептеу үшін 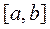 аралығын
аралығын 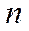 элементар аралыққа бөлеміз
элементар аралыққа бөлеміз 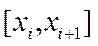 бұл жердегі
бұл жердегі 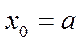 ,
, 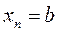 . АВСД төртбұрышының ауданы келесі формула бойынша есептеледі:
. АВСД төртбұрышының ауданы келесі формула бойынша есептеледі:
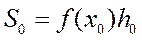 мұндағы
мұндағы 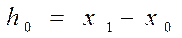 .
.
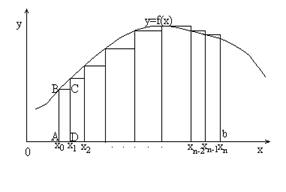
2.1 -сурет. Сол интегралдық қосынды
Кез-келген төртбұрыштың ауданы:
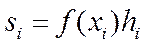
мұндағы 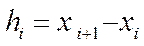 интегралдау қадамы. Онда сатылы фигураның ауданы:
интегралдау қадамы. Онда сатылы фигураның ауданы:
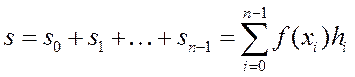
мұндағы 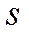 -интегралды қосынды деп аталады.
-интегралды қосынды деп аталады.
Бөлу нүктесін көбейтіп және барлық 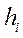 элементтерін нөлге ұмтылдырсақ онда сатылы фигураның жоғарғы шекарасы
элементтерін нөлге ұмтылдырсақ онда сатылы фигураның жоғарғы шекарасы 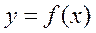 сызығына ауысады, сондықтан интегралды келесі түрде жазамыз:
сызығына ауысады, сондықтан интегралды келесі түрде жазамыз:
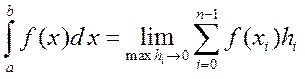 .
.
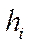 шеткі мәнге ие болған жағдайда, интегралдық қосындының көмегімен анықталған интегралдың мәнін келесі формула бойынша есептеледі:
шеткі мәнге ие болған жағдайда, интегралдық қосындының көмегімен анықталған интегралдың мәнін келесі формула бойынша есептеледі:

мұндағы екінші қосынды әдістің қателігі болып табылады. Ол қадамға байланысты болады.
(2.2) интегралды қосындысы сол қосынды деп аталады. Оң интегралды қосындыны алу үшін абцисса өсімен, 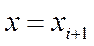 ,
, 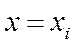 түзулерімен және
түзулерімен және 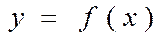 функциясымен құралатын сатылы фигураны саламыз.
функциясымен құралатын сатылы фигураны саламыз.
Оң интегралды қосынды бойынша есептеу формуласы:
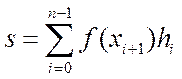 .
. 
2.2-сурет. Оң интегралдық қосынды
Сонымен қатар оң және сол төртбұрыштар әдістеріне қарағанда дәлірек әдіс болып саналатын орташа мәндер әдісі бар. Бұл әдісте 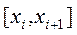 аралықтарындағы орта мән алынады:
аралықтарындағы орта мән алынады:

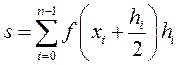 . (2.6)
. (2.6)
Трапеция әдісінде интегралдық қосындыны элементар трапециялардың аудандарының қосындылары ретінде қарастырамыз (2.3 -сурет):
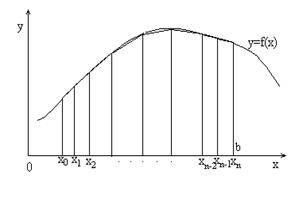
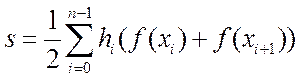
2.3-сурет. Трапеция әдісінің көрінісі
Y”=x2 +y2 екінші ретті дифференциалдық теңдеуді жуықтау
Х0= -1 y(-1)=2 y’(-1)=1/2
Y=f(x)
Y(x)= y(x0) + y’(x0)/1! (x-x0) + y”(x0)/2! (x-x0)2 +…+ y(n) (x0)/n! (x-x0)n +…
Y= 2 + 1/2 (x+1) + y”(-1)/2! (x+1)2 + y’’’(-1)/3! (x+1)3+ yiv(-1)/4! (x+1)4 +…
Y”(-1)= 1+22 = 5
Y’’’= 2x+2y* y’= -2+2*2*1/2 =0
yiv=2+2(y’)2 +2y*y”=2+1/2 +2*2*5= 45/2
Жалпы шешімі:
Y= 2 + (x+2)/2 + 5(x+1)2/2 + 45/48 (x+1)4
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|