Бірінші ретті дифференциалдық теңдеулер Коши есебі Айнымалылары шығарылытын теңдеулер

6.Бірінші ретті дифференциалдық теңдеулер Коши есебі Айнымалылары шығарылытын теңдеулер

Егер 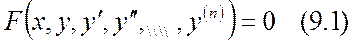теңдеуіңде n=1 болса , онда 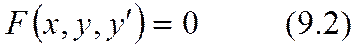теңдеуі бірінші ретті дифференциалдық теңдеу болады.

Немесе туындысы бойынша анықталған болса онда теңдеу мына 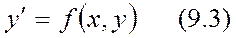түрінде жазылады.

Теорема. Егер функциясы 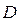аймағында анықталған, үзіліссіз және оның үзіліссіз дербес 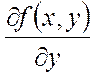туындысы болса, онда х₀нүктесінің 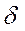- маңайы, яғни 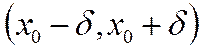табылып, теңдеудің бастапқы шарты қанағаттандыратын , яғни 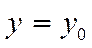егер 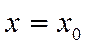шешімі бар және ол жалғыз болады.

Егер кез келген тұрақты С үшін 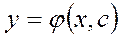функция бірінші ретті теңдеуді қанағаттандыратын болса онда осы функцияны дифференциалдық теңдеудің жалпы шешімі деп аталады.

Айнымалылары шығарылытын теңдеулер. теңдеуі бірінші ретті айнымалылары бөлінетін дифференциалдық теңдеу деп аталады. 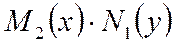көбейтіндісіне боліп (9.4) теңдеудің түріне келтіреміз: 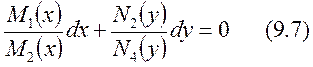. Енді осы теңдеудің екі жағын интегралдап жалпы интегралын табамыз: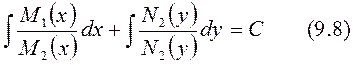

Мысал: xdy-ydx=0 дифференциалдық теңдеуді шешіңіз.

Шешімі: Бұл теңдеу (9.6) теңдеулер түріне жатады. Сондықтан теңдеудің екі жағын (ху) көбейтіндісіне бөлеміз, сонда 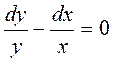теңдеуге келемізде жалпы шешімін табамыз: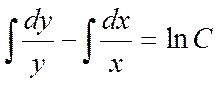

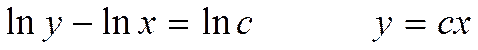
7.Бірінші ретті біртекті дифференциалдық теңдеулер

Бернулли теңдеуі.

b)Лагранж әдісі.Сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімін табу үшін практикада Лагранж (тұрақтыны вариациялау)әдісі қолдану ыңғайлы.

Алдымен берілген теңдеуге сәйкес біртекті теңдеудің жалпы шешімін табу керек. Алдында қарастырылғандай ол мына түрде жазылады:

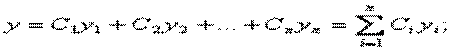
Содан соң, C_iкоэффициенттерін х-тің функциялары деп есептеп, біртекті емес теңдеудің дербес шешімін табу керек:

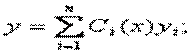
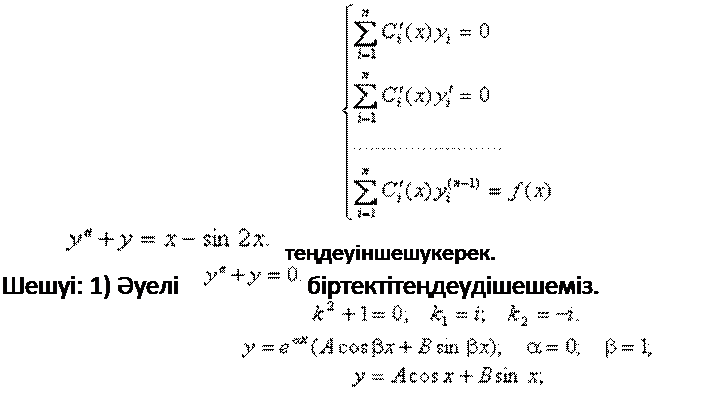C_i(x) функцияларын табу үшін келесі жүйені шешу керек:

2) Біртекті емес теңдеудің шешімі келесі түрде болады: 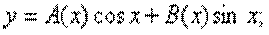Теңдеулер жүйесін құрастырамыз: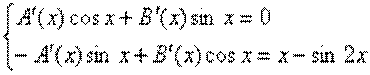

Жүйені шешейік: Енді В(х) функциясын табайық.

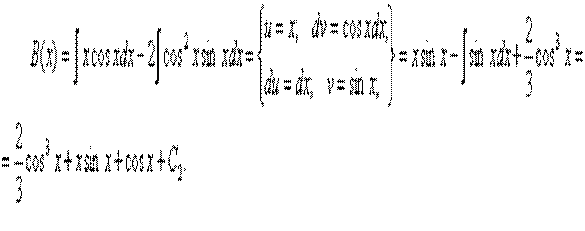
Табылған мәндерді біртекті емес теңдеудің шешімінің формуласына қоямыз:

Сөйтіп, біртекті емес теңдеудің жалпы шешімін дара шешімін таппастан жаздық.

7.c)Кейде біртекті емес сызықты дифференциалдық теңдеуді шешу үшін ^y^^uv алмастыруын (Бернулли әдісін)қолданамыз, яғни шешімді белгісіз екі функцияның кӛбейтіндісі түрінде іздейміз. Мұнда, туындыны y'= u'v +uv' өрнегімен алмастырамыз. _y_'+_P₍_x)y=Q(x)yⁿтүріндегі дифференциалдық теңдеу Бернулли теңдеуі деп аталады, мұндағы P(x),Q(x) - берілген үзіліссіз функциялар, n≠0, n≠1

Бернулли теңдеуінің сызықтық теңдеуден айырмашылығы оң жақ бӛлігінде у-тің белгілі бір дәрежесі бар, шешілуісызықтық теңдеулердегідей жүргізіледі. Шешімін табу үшін теңдеудің екі жағында _yⁿ -ге бөлеміз:

y'/yⁿ+P(x)y/yⁿ=y'y^-n+P(x)y^1-n= Q(x) (2.1)

Алмастыру жасаймыз: z=y¹^-ⁿ→ z'=(1- n)y^-ⁿ y'

Шыққан мәнді теңдікке қоямыз:

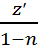+P(x)z=Q(x) -бірінші ретті сызықтық диф.теңдеу. Шыққан теңдеуді шеше отырып z-тітабамыз, z-тің табылған мәнін шешемиз.

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒