
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Екінші ретті дифференциалдық теңдеулер. Коши теоремасы
Мысал
у'+2у=е х у 2 - Бернулли теңдеуін шешу керек.
 Шешуі
Шешуі 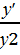 +
+ 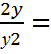 ex → у'y-2+2y-1= ex→ Z=y-1→z'=-y-2у' → -z'+2z= ex
ex → у'y-2+2y-1= ex→ Z=y-1→z'=-y-2у' → -z'+2z= ex
z '-2z=- ex немесеz '-2z=0-біртекті сызықтық дифференциалдық теңдеу
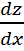 =2z→ dz=2zdx→
=2z→ dz=2zdx→ 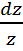 =2dx→
=2dx→ 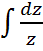 = 2
= 2 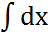 →lnz=2x+lnc→ lnz=lne2x+lnc→ lnz=lnexc→z=ce2x Енді тұрақты с-ны қандайда бір х-қа тәуелді функция деп аламыз,яғни c=t(x)→z=te2x=(te2x)'=t'e2x+2te2x→ z '-2z=- ex → t'e2x+2te2x=-ex→ t'e2x=- ex →
→lnz=2x+lnc→ lnz=lne2x+lnc→ lnz=lnexc→z=ce2x Енді тұрақты с-ны қандайда бір х-қа тәуелді функция деп аламыз,яғни c=t(x)→z=te2x=(te2x)'=t'e2x+2te2x→ z '-2z=- ex → t'e2x+2te2x=-ex→ t'e2x=- ex →
 e2x=-e→ e2xdt=-txdx→dt=-
e2x=-e→ e2xdt=-txdx→dt=- 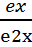 dx→dt=-e-xdx→
dx→dt=-e-xdx→ 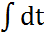 =-e-xdx→t=e-x+C1
=-e-xdx→t=e-x+C1
Z=( e-x+c1)e2x= ex+c1e2x→y-1= ex+C1 e2x→1/y= ex+C1e2x→y=  .
.
 8.Толық дифференциал түріндегі бірінші ретті диф-қ теңдеулер. Толық дифференциал түріндегі бірінші ретті дифференциалдық теңдеулер
8.Толық дифференциал түріндегі бірінші ретті диф-қ теңдеулер. Толық дифференциал түріндегі бірінші ретті дифференциалдық теңдеулер
С) (x+y)dx+xdx=0
P(x,y)=x+y
Q(x,y)=x
P`y=1 y’=u’x + u
Q`x=1 1+u + u’x+u=0
P`y=Q`x u’x+1+2u=0
U(x,y)=∫(x+y)dx+ϕ(y) Осындай әдіспен де шешуге болады.
U(x,y)=x2/2 +xy+ ϕ(y)
X+y(y)=x
ϕ`(y)=0
ϕ(y)=0
U(x,y)=x2 /2 + xy+C
(x2 /2 + xy+C) / xdx=1+ 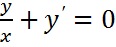
u=y/x
Мысалыe-ydx+(1-xe-y)dy=0теңдеуінің жалпы шешімін табу керек.
Берілген жағдайда P(x,y)= e-y, Q(x,y)=1- xe-y болғандықтанP’y=- e-y,Q’x=e-yяғниP’y=Q’x . Сондықтан берілген теңдеудің сол жағы кейбірU(x,y) функциясының толық дифференциалы болып,U’x=e-y, U’y=1-xe-y теңдіктері орындалады. Бұл теңдіктердің біріншісін интегралдасақU(x,y)=ʃe-ydx+φ(y) немесе U(x,y)=xe-y+ φ(y), мұндағы φ(y)кез келген функция. Шарт бойыншаU’y=1-xe-y болу керек, яғни .–xe-y+φ’(y)=1-xe-y,
 φ’(y)=1φ(y)=y+c1.СоныменU(x,y)=xe-y+φ(y)=
φ’(y)=1φ(y)=y+c1.СоныменU(x,y)=xe-y+φ(y)=
xe-y+y+c1. Демек, теңдеудің жалпы шешіміxe-y+y+c1=c2 немесеxe-y+y=c, мұндағыc=c2-c1
9. Екінші ретті дифференциалдық теңдеулер. Коши теоремасы

1. Жалпы жағдайда 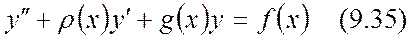 теңдеуді екінші ретті сызықты біртекті емес дифференциалдық теңдеу деп аталады. Мұндағы
теңдеуді екінші ретті сызықты біртекті емес дифференциалдық теңдеу деп аталады. Мұндағы 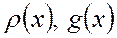 және
және 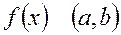 интервалында үзіліссіз функциялар. Ол егер
интервалында үзіліссіз функциялар. Ол егер 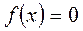 онда
онда 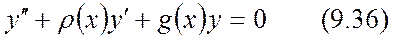 екінші ретті біртекті сызықты дифференциалдық теңдеу (9.35), (9.36) теңдеулер арасында
екінші ретті біртекті сызықты дифференциалдық теңдеу (9.35), (9.36) теңдеулер арасында 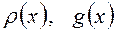 тұрақты мән қабылдайтын жағдайды қарастырамыз, сондықтан
тұрақты мән қабылдайтын жағдайды қарастырамыз, сондықтан 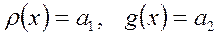 тұрақты сан болсын және
тұрақты сан болсын және 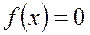 тең болатын болсын, онда (9.36) теңдеу
тең болатын болсын, онда (9.36) теңдеу 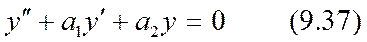 түрін қабылдайды.
түрін қабылдайды.
9.37) теңдеуін коэффиценттері тұрақты біртекті сызықты екінші ретті дифференциалдық теңдеу деп атайды. Бұл (9.37) теңдеудің шешімін Эйлер тәсілі бойынша 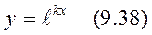 түрінде іздейміз. Онда
түрінде іздейміз. Онда 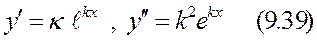
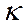 - белгісіз тұрақты сан. (9.38) және (9.39) дифференциалдық (9.37) теңдеуді қанағаттандыруы керек. Сондықтан
- белгісіз тұрақты сан. (9.38) және (9.39) дифференциалдық (9.37) теңдеуді қанағаттандыруы керек. Сондықтан 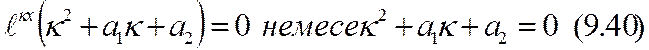 теңдеуі шығады. (9.40) біртекті сызықты дифференциалды теңдеуге сәйкес сипаттаушы теңдеу деп аталады.
теңдеуі шығады. (9.40) біртекті сызықты дифференциалды теңдеуге сәйкес сипаттаушы теңдеу деп аталады.
Егер 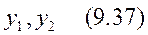 теңдеудің шешімі болса, онда екі шешім өз ара сызықты тәуелсіз деп аталады, егер екеуінің қатынасы тұрақты болмаса яғни .
теңдеудің шешімі болса, онда екі шешім өз ара сызықты тәуелсіз деп аталады, егер екеуінің қатынасы тұрақты болмаса яғни . 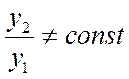
Анықтама. Егер 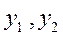 өзара сызықты тәуелсіз (9.37) теңдеудің шешімі болса, онда ол теңдеудің жалпы шешімі
өзара сызықты тәуелсіз (9.37) теңдеудің шешімі болса, онда ол теңдеудің жалпы шешімі 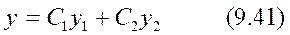 түрінде жазылады.
түрінде жазылады.
1.Егер сипаттаушы теңдеудің 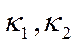 шешімдері әртүрлі және нақты сандар болса, онда (9.37) теңдеудің жалпы шешімі
шешімдері әртүрлі және нақты сандар болса, онда (9.37) теңдеудің жалпы шешімі 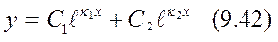 түрінде жазылады.
түрінде жазылады.
Y”=f(x) ретін интеграл арқылы төмендетеміз.
Y’= 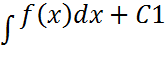
Y= 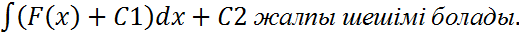
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|