Жинақты болудың қажетті шарты.

Жинақты болудың қажетті шарты.

Теорема. Егер 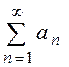қатары жинақты болса, онда оның 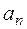жалпы мүшесі нөмірі шектеусіз өскенде нолге ұмтылады, яғни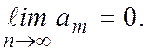

Дәлелдеу.Айталық 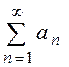қатары жинақты және оның қосындысы 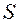болсын. Оның 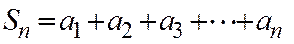ж\е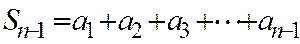

дербес қосындыларын қарастырайық.Бұлардан 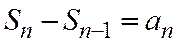Сондықтан,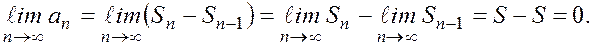

Өйткені 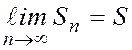және 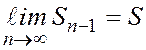. Мұн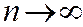да -да 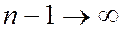. Соным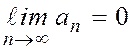ен, екен.

Шынында, егер қатарды жинақты десек, онда алдыңғы теоремаға сәйкес қатардың жалпы мүшесі нолге ұмтылған болар еді. Бірақ, бұл шартқа қайшы. Сондықтан, қатар жинақсыз.

Гармоникалық қатар - 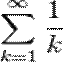сандық қатары. Гармоникалық қатар әрбір мүшесі (екіншісінен бастап) өзімен көршілес екі мүшенің гармоникалық орта мәні болады. Гармоникалық қатар жинақсыз және оның дербес қосындылары 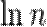санындай өседі:

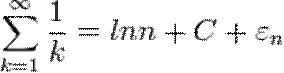,мұндағы және С саны Эйлер тұрақтысы деп аталады. 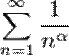— қатары жалпыланған гармоникалық қатар деп аталады, бұл қатар α>1 болғанда жинақталады және α≤1 болса жинақталмайды.

Мысал. 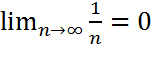болса да 1 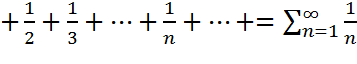гармоникалық қатардың жинақсыз екенін дәлелдеу керек.

Шешуі. S_2nжәне S_n дербес қосындыларының айырмасын бағалайық:

S_2n-S_n= .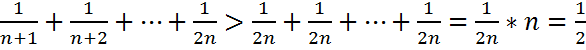

Яғни p=n болғанда қатар үшін Коши кретерийі орындалмайды,демек қатар жинақсыз.

12.Сандық қатары және оның жинақтылығы

Ақырсыз қатарлардың жинақталу белгілерін зерттеуді мүшелері теріс емес сандар болатын қатарлардан бастаймыз. (1) қатар мүшелері а≥0, n=1,2… дейік. Сонда бұл қатардың s_n (n=1,2….) бөлік қосындыларының кемімейтіні анық. Бұл жағдайда мына тұжырым орындалады: мүшелері теріс емес (1) қатар жинақталатын қатар болуы үшін оның бөлік қосындылары жоғарыдан шенделген болуы қажетті және жеткілікті.

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒