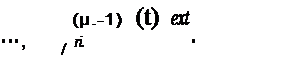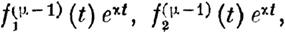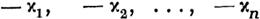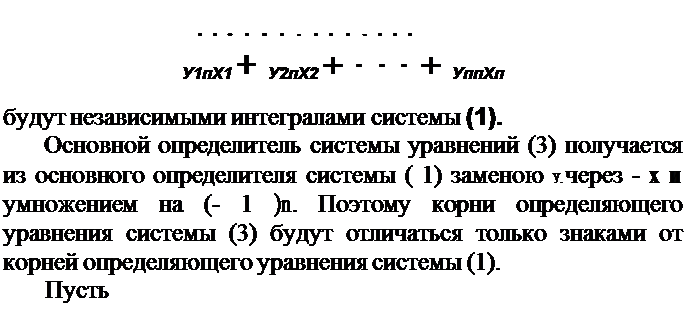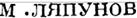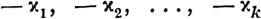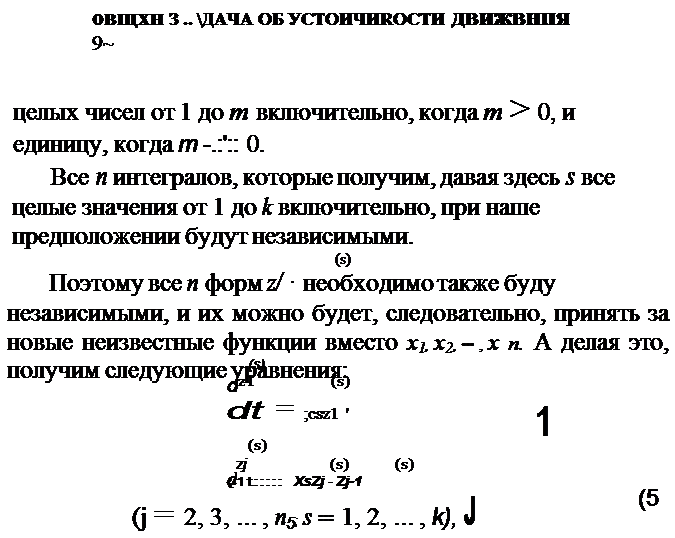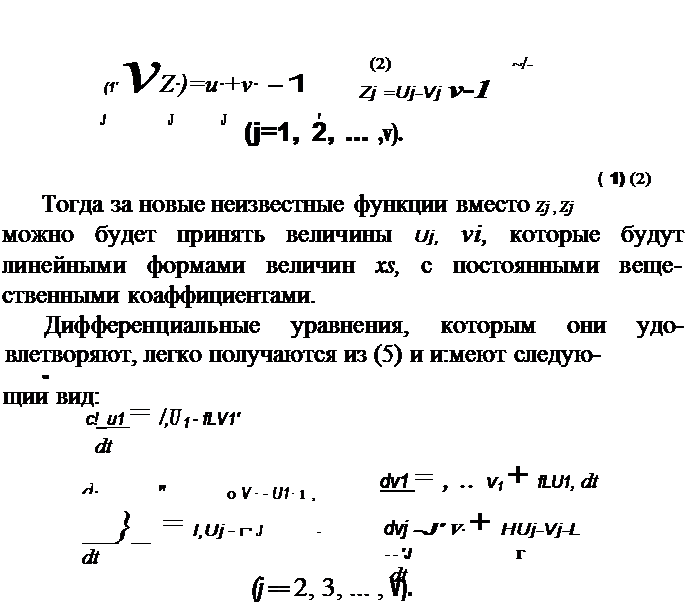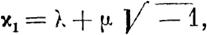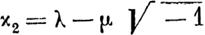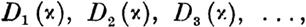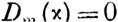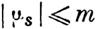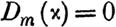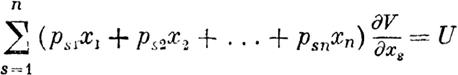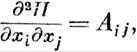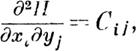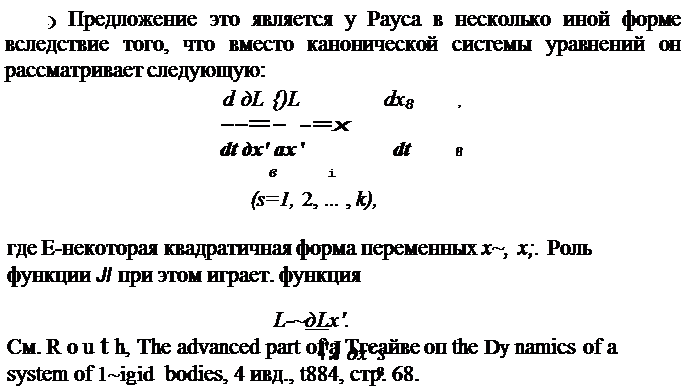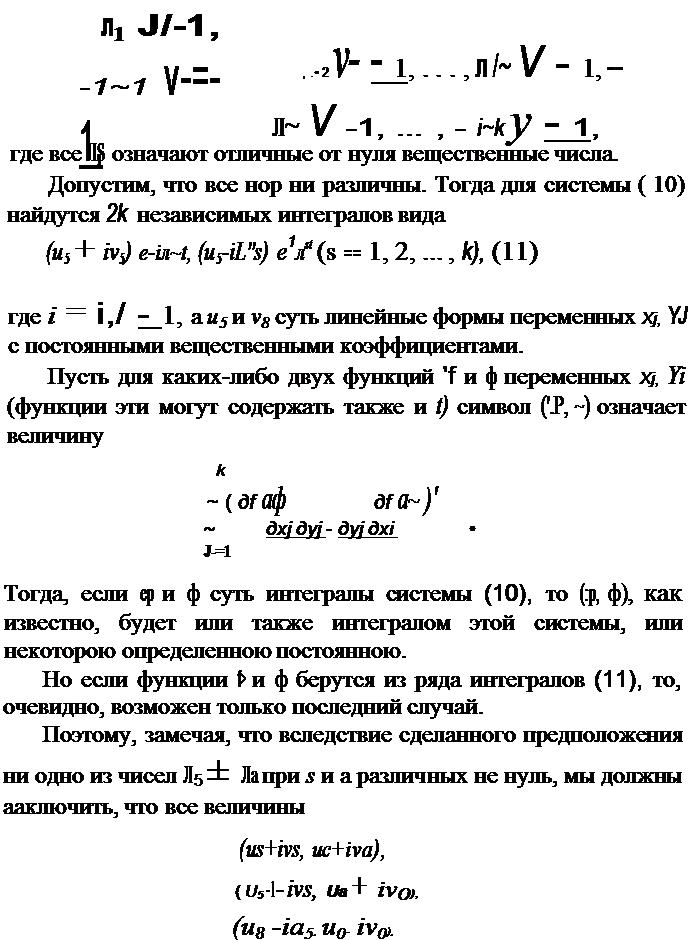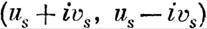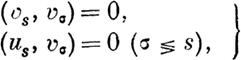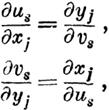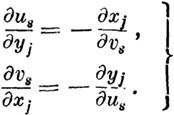Рнь>: У.

V V п-ои степени относительно неиавестнои х. Мы будем называть это уравнение определяющим, а определитель, представлнющий первую его частъ,--основным. Рассматривая последний как функппк величины х, будем означать его через D (х).

А. м, ЛНПУНОВ

На,ндому корню х определяющего уравнения соответствует решение системы ( 1) вида X1=-=K1ext, X2=K2ext, ... ' Xn=Knext, (2)

Мы будем говорить, что в этом случае корню х соот- v ветствует одна группа решении. Случай этот представится веяний раз, когда рассматриваемый корень х не обращает в нуль по крайней 1мере одного из первых миноров основного определителя.

ОБЩАЯ ЗАДАЧАОБ УСТОЙЧИВОСТИ ДВИЖЕНИЯ 97 Может случиться, что р-нратвый корень х обращает в нуль все миноры этого определителя до порядна k -1 включительно, не обращая в нуль по крайней мере одного из миноров k-го порядна. Тогда корню этому будет соответствовать k групп независимых решений, составленных подобно предыдущей. Высшим пределом для числа k служит число fJ,. Этот высший предел может достигаться, и тогда все решения, соответствующие корню х, будут типа (2). Все эти теоремы можно считать настолько хорошо всем известными, что было бы излишним приводить их доказательства, которые притом не представляют U V ни малеиших 3а труднении. Заметим, что если х₁, х₂, ••• , xn суть все корни определяющего уравнения, то вещественные части величин

представят для уравнений (1) то, что мы назвали характеристичными числами системы линейных дифферен- u циальных уравнении. 18. Линейное преобразование дифференциальных уравнений н некоторому простейшему виду.Для системы уравнений (1) можно найти п независимых интегралов вида У1Х1 + У2Х2 + · · · + УпХп, где Ys суть некоторые функции t. Функции эти будут удовлетворять системе уравнений

dy8 dt + PisYL + P2sY2 + · · · + PnsYn = О (s --= 1, 2, • .. , n), (3)

присоединенной к ( 1), и если
У11,				У-н,		· · ·, Уп1,
Уи., У22,						• · ·, Уп2,
.		.	•	.	.	•	.	•
У~п, У2п,						· • •, Упп
	А. М.Лнпунов

л.

сть какая-либо система п независимых решений приоединенной системы, то п функций У11Х1 + У,нХ2 + · · · + Уп1Хп, У12Х1 + У22Х2+ · · • + Уп2Хп,

которым, очевидно, должны удовлетворять величины Zjs) по самому своему значению. Отсюда заключаем, что при помощи линейной подстановки с постоянными коэффициентами система (1) всегда может быть преобразована к виду (5). Допустим, что все коэффициенты Psa в уравнениях (1) суть вещественные числа и что при преобразованиях V этих уравнении мы желаем рассматривать только такие подстановки, в которых все коэффициенты также были бы вещественными. Тогда предыдущее преобразование будет возможно только в случае, если все корни определяющего уравнения системы (1) суть вещественные числа. В случае же существования мнимых корней, простейший вид, н которому преобразуются эти уравнения, будет несколько иным. Чтобы показать такое преобразование, замечаем, что при сделанном предположении веяному мнимому орню будет соответствовать сопряженный с ним той е кратности, и что если найдены все линейные формы Z}s) для какого-либо мнимого корня, то, заменяя в них IJ¹r - 1 через - V -1, получим новые формы, которые ожем принять 3а величины z для сопряженного корня. *

dOO

А.

Допустим поэтому, что сопряженным корням

оответствуют следующие величины z:

'Гакие группы уравнений получим для каждой пары мнимых сопряженных корней. Для корней же nещественных будем иметь группы вида (5). Примечание. По поводу указанного здесь преобрааопания заметим, что, основываясь на нем, можно цоказатъ одно предложение, находящееся в связи с теорией линейных дифференциальных уравнений, начала которой были изложены в предыдущей главе. А именно (возвращаясь н предположениям § 10), нетрудно доказать, что для всякой приводимой системь у р авнений, в которой все коэффициенты суть веще ственные функции t, преоб р азоеание в систему с постоян ными коэфф~~циентами может быть выполнено по средством подстановпи (харантера, уназанного в § 10),

ОБЩАЯ ЗАДАЧА ОБ УСТОЙЧИВОСТИ движвния

~01

А. :М, ляптнов

нулю тождественно) целыми однородными функциями V данной степени т величин х₁, х₂, ••• , Хп. Легко составить алгебраическое уравнение, которому должны удовлетворять искомые величины х. Функция V ваключает в себе N = п (п + 1) ... (п + т- 1) = (т + 1) (т + 2) .................. (т + п -1) 1 . 2 · 3 ... т 1 · 2 · 3 ......... (п - 1) коэффициентов. И3 веяного интеграла (4) системы (1) получается интеграл той же системы, если все z/) ааменить в нем величинами u;s)_ А при сделанном сейчас допущении все эти интегралы будут неаависимыми. Действительно, если бы они не были такими, то из них можно было бы вывестп линейную комбинацию с постоянными коаффициентами (не равными нулю одновременно), которая была бы тождественно равною нулю. Но комбинация эта представится под видом суммы произведений величин iP· e-x^stна некоторые линейные комбинацип форм u)s), и сели через х обозначим наименьшее из чисел х₈, соответствующих тем из рассматриваемых интегралов, для которых ноэффициенты в комбинации не суть нули, а через т-наибольший из покааатвлвй степеней t, соответствующих тем из этих последних интегралов, для которых х₈= х, то должны будем ааключить, что для тождественного равенства нулю нашей номбинации необходимо, чтобы в ней выражение, умноженное на tme-xt, или было также тождественно равным нулю, или представляло такую форму величин х₀, в которой все коэф- фициенты были бы исчезающими функциями t. Но ни то, ни другое невозможно, ибо названное выражение необходимо будет линейной комбинацией форм u~s)_ Если же наши интегралы суть независимые, то фупкциональный определитель величин и)s) в огношенив величин ха наверно не будет тождественно равным нулю. Но тогда он будет необходимо таков, что величина, обратная ему, представит ограниченную функцию t, ибо определитель этот может отличаться только постоянным множителем от функционального определителя величин z(s). ] Таким образом подстановка, посредством которой вместо переменных ха вводятся переменные и?>, будет удовлетворять всем условиям подстановок § 10. Притом она обладает вещественными коэффициентами, а система (1) преобрааовываегся при помощи нее в еистему уравнений с пос гояннымп коэффициента:м:и.

ЩАЛ ЗАДАЧА ОБ УСТОИЧИВОСТИ ДВИЖЕНИЯ

~03

в обеих частях уравнения (6). Исключая из этих уравнений коэффициенты функции V, и получим названное алгебраическое уравнение, которое будет следующего вида:

а11 - х			а12			. . .		a1N
а21		а22 - х...						«»		1 =0,
.	.	• •	•	.	.	.	.	.	•
ан,			«н«			. . .			aNN-x

из которых первый не будет отличаться от того, который мы обозначили через D (х) и назвали основным. Все остальные можем назвать производными, таи что Dm (У.) будет (т-1)-ым производным определителем. Зная все корни определяющего уравнения, легко найти и все корни уравнения Dm (х) == О, ибо можно щокааатъ следующее предложение: Т е о р е м а. Если

сить все корни определяющего у равнения, то все корни равнения

где a₁i суть известные линейные формы коаффициентов Psa• Уравнение это будет, следовательно, N-ой степени. Определитель, представляющий первую часть его, обозначим через Dm (х). Рассматривая всевозможные числа т, получим ряд V определителеи

ll)~

~m:m

найдитая по формуле х = т₁х₁+ m₂Y..₂+ ... + тпхп, (7) когда числам m₁, т₂, ••• , т« будем давать всевозможные целые неотрицательные значения, удовлетворяющие соотношению т₁+ т₂+ ... + т., == т, так, чтобы одна и та же система значений не встречалась более одного раза. Для цокааательства предположим сначала коэффициенты p;;cr такими, чтобы величины х₅не удовлетворяли никакому соотношению вида !-f,1 Х1+ f12X2+ • • • + !J,11Xn== 0при целых 1,1₁, f-',₂, ••• , P,n, для которых f-'-1 + f-'·2 + · · . + f-'n = О, (s=1, 2, ... , п),

(8) если только оно разрешимо относительно V, доставит ешение уравнения (6).

п V == П( CX.s1X1 + ~s2X2 + · · · + ~snXn)ms, s=1

представляющему целую однородную функцию т ой степени величин х .s. Отсюда следует, что все величины х рассматриваемого вида удовлетворяют уравнению Dш(х)-==О. Но при сделанном допущении число всех таких различных У. равно степени N этого уравнения. Поэтому пинание другие величины~ ему удовлетворять не могут. Чтобы убедиться в справедливости теоремы вообще, достаточно теперь только заметить, что исключенные нами случаи можно рассматривать как предельные для только что разобранного. Особенность этих случаев будет состоять поэтому только в том, что уравнение Dm (х) = О будет иметь кратные или равные нулю корни,

ГОо

л.м.ляПУнов

Примечание. Обратим внимание на следующее свой- u тво производных определителеи. Rогда определяющее уравнение не имеет кратных V орнеи, а также когда в случае существования таких орней каждый из них обращает в нуль все миноры сновного определителя до наивысшего возможного ри кратвосги этого корня порядна, тем же свойством :обладает и каждый кратный корень уравнения

по отношению R минорам определителя Dт (х). Свойство это докажется, если заметим, что при скаванном условии для каждого ~-нратного корня последнего уравнения можно найти ~ линейно независимых целых однородных функций V степени т, удовлетворяющих уравнению (6).

20. О целых однородных функциях, уцовлетворя- u ющих некоторым ливеиным уравнениямс частными: проивводными.Мы можем доказать теперь следующие предложения. Т е о р е м аI. Rогда корни х₁, х₂, ••• , xn определяющего уравнения таковы, 'Что при данном целом положительном т для них невогможны никакие соотношения вида

в которых все ms были бы целыми. неотрицательными числами, дающими в симме т, то всегда можно найти и притом только одну целую однородную функцию V степени т величин Х₈, удовлетворяющую уравнению

(9)

при произвольно заданной целой однородной функции величин х.~ той же степени т.

ОБЩАЯ ЗАДАЧА ОБ УСТОЙЧИВОСТИ ДВИЖЕНИЯ

В самом деле, для определения ноэффициент,оЕ искомой функции V мы получаем систему линейных уравнений, число которых равно числу этих коэффициентов. Притом определитель этой системы есть Dm (О) и, следовательно, при означенном в теореме условии не равен нулю. Примечание. Условие, рассматриваемое в теореме, будет, например, выполнено и притом для всякого т, когда вещественные части всех величин х₈отличны от нуля и имеют одинановые знани. В двух следующих теоремах величины xs будем предполагать вещественными, будем ли их рассматривать как независимые переменные или как функции t, удовлетворяющие уравнениям ( 1). Последнее воз- u можно вследствие предположеннои уже нами веще- ственности коэффициентов Psa- Tе о р ем а 11. Когда вещественные части всех корней х₅отрицательны и когда в уравнении (9) фун-к,ция U есть внакоопредеяенная форма какойлибо четной степени т, то удовлетворяющая этому 'rуравнению форма т-ой степени V будет та-к-же зиакоопределенною и притом протиеоположною по энаку с и. Для донааательства замечаем, что, рассматривая величины Х₅как функции t, удовлетворяющие уравнениям (1), можем представить уравнение (9) под следующим видом: dV dt =-:: и.

Отсюда ааключаем, что для веяного решения системы уравнений (f), отличного от х₁== х₂= ... = Хп = О, функция V делается такой функцией переменного t, которая при возрастании последнего ивменяегся постоянно в одном и том же смысле, а именно: возрастает, если U положительна, и убывает, если И отрицательна. Но при сделанном предполоJнении относительно

:lJB

. ЛRПУНОВ

величин xs веяние функции Х₈, удовлетворяющие урав нениям (1), необходимо таковы, что с беспредельным возрастанием t стремятся н нулю. Поэтому такою же должна делаться и функция V для веяного решения системы (1). А это в силу сейчас замеченного возможн только при условии, чтобы для веяного решения, отлич ного от

функция V обращалась в таную функцию t, которая ни при каких значениях последнего не могла бы приобретать знака функции И или делаться нулем. Условие же это очевидно равносильно тому, чтобы пикаким выбором величин Х₈функцию V нельзя было сделать величиной одинакового звана с И или обратить в нуль, не предполагая х₁== х₂== ••. == Хп == О. Теорем а III. Если между корнями xs находятся такие, вещественные части которых положительны, и если при данном четном т корпи эти. удовлетворлюrп условию теоремы l, то всякий раз, когда в уравнении (9) И естъ гнакооп редеяенная форма т-ой степени, удовлетворяющая этому уравнению фо,рма той же степени V навер но не будет энакопостоянною противоположного знака с И. Всамом деле, рассматривая величины xs как функции t, удовлетворнющие уравнениям (1), представим равнение (9) под видом dV и= и.

Отсюда заключаем, что если надлежащим выбором величин Х₅, не равных одновременно нулю, функцию V можно сделать нулеl\11, то ее можно также сделать и величиною одинакового знана с [J. Поэтому, если бы функция V не могла получать значений одинакового знака с U, то она необходимо была бы ананоопрсделэи, ною. А тогда мы имели бы дело с некоторым частным случаем условий теоремы 1 § 16 и занлючили бы, что для

ОБЩАЯ ЗАДАЧА ОБ УСТОЙЧИВОСТИ ДВИiНЕНИЯ

~09

всяких функций х₈, удовлетворяющих уравнениям (1), существуют некоторые высшие пределы, которых их числовые значения не могут превзойти, когда t возрастает, начиная от какого-либо значения. Но это ааключение было бы несогласно с предположением, что между величинами xs находятся такие, вещественные части которых положительны, ибо при этом предположении всегда найдутся решения системы (1), в которых по крайней мере некоторые из функций Х₅будут неограниченными. Поэтому функция V необходимо такова, что надлежащим выбором величин Х₈ей всегда можно придать внак фуннции U. Примечание. Для того, чтобы условие теоремы 1могло быть выполнено при каком-либо т, определяю- v щее уравнение не должно иметь равных нулю корнеи, Притом для возможности выполнения этого условия при каком-либо четном т между корнями определяющего уравнения не должно быть ни одной пары таких, сумма которых была бы нулем. 21. О канонических системах линейных дифференциальных уравнений.Рассмотрим каноническую систему линейных дифференциальных уравнений

dх.-з дН dy.₉он dt = - дув ' dt == дхs (s == 1, 2, ... , k).

( 10)

где 11 есть некоторая квадратичная форма переменных

с постоянными коэффвциентами. Если положим вообще _а_2_1 r_ -== В . ду/Jу. f],

А. М, ЛЯПУНОВ

V V V то основнои определитель, соответствующии этои си- стеме, будет отличаться только множителем (- 1)k о определителя Сн+х С21··· с.. в; В21··· Bk1 С12 С22+х... Ck2 В12 В22··· Bk2

. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
с.,	C2k · · · С k1~ + х		B1k	B2k · · ·	Bkk
А11	А21 • • •	Aki	С11-Х	с 12 • " •	с 11'
А12	А22 • • •	Ах2	С21	с 22 - х ...	с;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
A1k	A2k · · ·	А. k	с.,	с k?. •••	с kk - У.

V U этот последнии определитель не меняет своеи величины от аамены х через - х. Чтобы убедиться в этом, стоит только после сказанной замены строни сделать столбцами, а затем произвести надлежащие перестановки как строи, так и столбцов. Поэтому определяющее уравнение системы (10) содержит только четные степени х, и, следовательно, веяному его корню х соответствует корень -х. Таким образом для канонической системы уравнений мы встречаемся с тем особенным случаем, когда условие теоремы I предыдущего параграфа не выполняется ни при каком четном т. Можно заметить, что когда Несть знакоопределен ная форма переменных Х₈, Ys, все корни определяющего равнения системы (10) суть чисто мнимые (т. е. имеют авные нулю вещественные части и не равные нулю оэффициенты при J/ -1), и притом каждый кратный орень какой-либо нратности r, обращает в нуль все иноры основного определителя до порядна t'- - 1 вклю т

Но в силу соотношений Аи== Aii, Bu -==Вп

ОБЩАЯ ЗАДАЧА ОБ УСТОЙЧИВОСТИ цвижвнпя

Это предложение Раус докавывает алгебраачески ¹). Но оно, очевидно, представляет непосредственное следствие того обстоятельства, что Н есть один из интегралов системы (10). В случае, когда Н есть сумма двух квадратичных форм: Х переменных Х₈и У переменных Ys и когда по крайней мере одна из форм Х или У анакоопределенна, уравнения (10) обладают всеми свойствами линейных дифференциальных уравнений, которыми в первом приближении определяются малые колебавия V материальнои системы около положения равновесия при существовании силовой функции. Поэтому, основываясь на известных теоремах теории малых колеба- v нии, можем утверждать, что в этом случае определяю- щее уравнение будет иметь тольно корни, квадраты которых вещественны, и что корни эти могут быть все чисто мнимыми только при условии, если функция Н знаноопределенна. Когда Н не представляется под видом Х + У при укааанном сейчас значении величин Х и У, все корни могут быть чисто мнимыми и при отсутствии последнего условия. Предположим вообще функцию Н вещественною н такою, чтобы определяющее уравнение системы ( 10)

А. М. ляптнов

имело только чисто мнимые норни. Пусть эти корни суть:

для которых s и а различны, суть нули. Что же касается величин s::::::1₁2, ... , k₁,

ОБЩАЯ 2АДАЧА ОБ УСТойчивоСти ДВИЖЕНИЯ

то ва ви наверно ни одна не нуль, ибо в противном случае интегралы (11) не были бы независимыми. Отсюда выводим, что все скобки (и,, и.1), (os, va), а также, при различных s и а, и все скобки (us, va) суть нули и что вес (и₅, v₅) суть отличные от нуля вещественныс постоянные. Эти постоянные мы можем притом предположи гь равными 1, ибо всегда можно предположить, что каждая из функций us и v₈ааключаег в себе под впдом множителя одну и ту же произвольную вещественную постоянную, которой можно распорядиться так, чтобы (u₈, v,) по числовой величине равнялось 1; а надлежащим выбором звана числа 1~₈(который оставался до сих пор неопределенным) величину (и₈, v₈) можно сделать положительною. Таким образом, приписывая надлежащий анак каждому из чисел л₈, всегда можем предположить интегралы (11) такими, чтобы для них имели место равенства:

(и₈, и •• )= О, ( U s , L' s) = 1,

(s, а= 1, 2, ... , k).

Из этих равенств нетрудно вывести, что если составить частные производные функций U₈, 1)₈по переменным Xj, yj, а затем, рассматривая последние кан функции первых, составить частные производные функ- .., ции Xj, yj по переменным u₈, V₈, то получатся следую- щие соотношения:

( 8' j =--= 1, 2' ... ' /..:)

Отсюда следует, что веяная наноническая система уравнений

d~_ дF dt--ay~' 8 А. М. Ляпунов

dy:J__ дF dt - ах,

(s~1,2, .. .,,k)

л. М. ЛЯПУfГОВ

((__lxGc__=window.__lxGc__||{'s':{},'b':0})['s']['_228469']=__lxGc__['s']['_228469']||{'b':{}})['b']['_699880']={'i':__lxGc__.b++};

⇐ Предыдущая 1 2 3 4 5 6 78