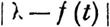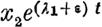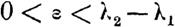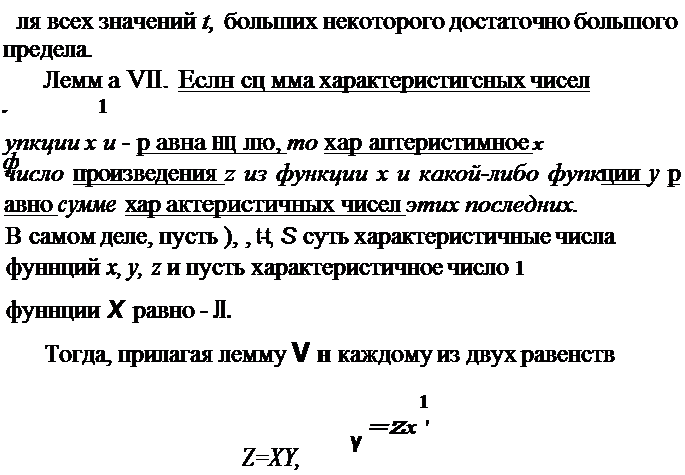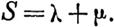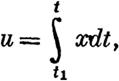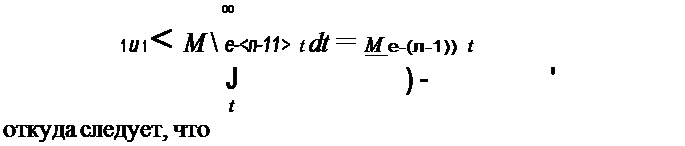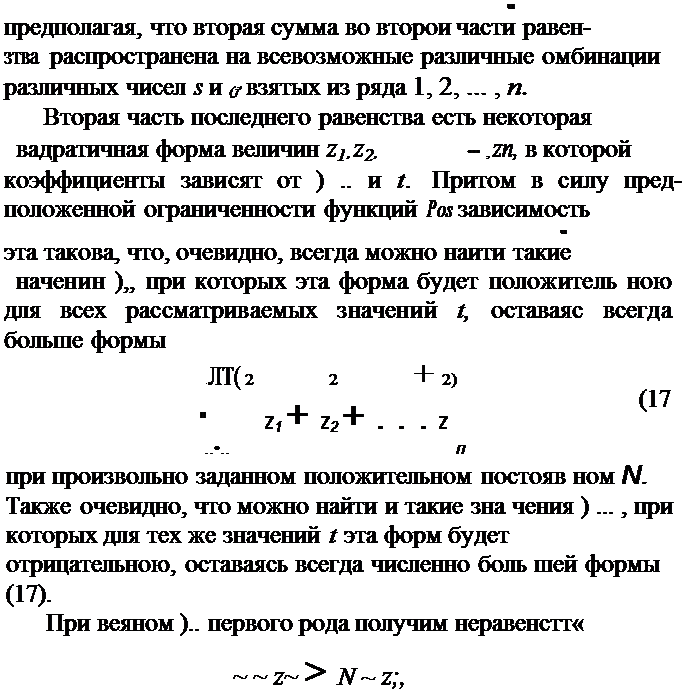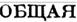Рнь>: У. 3 страница

ОБЩАЯ ЗАДАЧА ОБ УСТОЙЧИВОСТИ ДВИЖЕНИЯ

выбранная нами система частных решений уравнений (6) такова, что при t = t₀ xii = 1, xu = О (i :;;;: j). В последнем предположении постоянные as суть значения функций х для t = to. Мы можем поэтому утверждать, что если все А₅суть непрерывные функции t, и если А₀есть наименьшее из значений, принимаемых ими для t = t₀, то при всяких а₈, которые по числовым значениям меньше А₀, найдется такой предел Т, больший t₀, что фувкции Х₈, удовлетворяющие уравнениям (1) и принимающие значения as при t == t₀, представятся абсолютно сходящимися рядами, расположенными по восходящим степеням этих значений, для веяного t, лежащего между t₀И Т. П'римечание. Для представления функций », в тех же пределах изменяемости t можно конечно получить бесчисленное множество других абсолютно сходящихся рядов, расположенных по целым положительным степеням некоторых других постоянных произвольных а.₁, а₂, ••• , ап, модули которых достаточно малы. Веяние ряды такого характера могут быть выводимы из предыдущих при помощи подстановок вида as = f s (а.1, а₂, •.. , осп)· (s = 1, 2, ... , п), (14) где f s означают некоторые голоморфные функции величин tXa• Рассматривая нвние-либо ряды этого рода, допустим, что для них все функции / s при Cl₁::::; а₂=== ••• ... = ап = О делаются нулями. Допустим кроме того, что функциональный определитель функций / s в отношении величин rx₀при таком положении не делается нулем. Тогда, если в этих рядах возьмем совокупности всех членов не выше т-го порядна относительно постоянных а₀, то эти совокупности представят то, что мы будем называть выражениями функций Х₅в т-ом приближении. 3 А. М. Ляпунов

А.М.ЛНПУНОВ Известно, что при сделанных предположениях отв сительно функций fs уравнениям (14) всегда можн удовлетворить, выбирая для величины a,cr некоторы голоморфные функции величин as, уничтожающиеся при: а, == а2 = ... = ап == о, и. что, когда все I C'ta 1, 1 as 1 подчинены условию не превосходить некоторых достаточно малых пределов, гакое решение будет единственно возможным. Поэтому различные т-ые приближения, полученные u из различных разложении рассматриваемого характера, будучи выражены через постоянные а₈, представятся рядами, расположенными по целым положительным степеням последних, и ряды эти будут разниться между собою только членами выше т-го порядна. 5. Более определенная постановка задачи. Движения установившиеся и периодические. Две категории способов исследования устойчивости. При той общей точке зрения, с наной мы рассматривали вопрос до сих пор, мы имели в виду только докааатъ, что по крайней мере для t, не выходящего из известных границ, всегда существуют функции, удовлетворяющие уравнениям ( 1) и в данный момент принимающие какие-либо данные, численно достаточно малые значения, и что метод последовательных приближений доставляет ряды, которые при известных условиях могут служить для определения этпх функций. Но переходя н изложению наких-либо способов решения вопросов об устойчивости, мы должны будем оставить эту точку зрения, ограничивая нашу задачу некоторыми более определенными предположениями относительно дифференциальных уравнений возмущенного движения. Преимущественно мы будем заниматься рассмотрением двух следующих случаев: когда все коэффи- циенты Pscr, P~mi, · ··' тп) суть постоянные величины и когда это суть периодические функпии t с одним и тем же вещественным периодом. Первый, конечно, можно было бы рассматривать кан астный случай второго. Но по многим причинам мы предпочитаем рассмотреть его отдельно.

ЩАЯ ЗАДАЧА ОБ УСТОЙЧИВОСТИ ДВ:йЖЕНИЯ

В первом случае, по примеру Рауса, невозмущенное движение мы будем называть (для величин, по отношению н которым исследуется устойчивость) установившимся; во втором-периодически.м. Рассматривая эти два случая, увидим, что для решения нашего вопроса весьма существенное значение будет иметь исследование первого приближения. Мы покажем, при каких условиях это исследование вполне решает вопрос об устойчивости и при каких оно вообще делается недостаточным. Вместе с тем укажем и некоторые способы для решения вопроса в известных случаях этого последнего рода. Прежде, однвно, чем перейти н детальному рассмотрению вопроса, мы остановимся на некоторых общих предложениях, которые послужат точками отправления при наших изысканиях. Все способы, которые мы можем укааать для решвния занимающего нас вопроса, можно разделить на две категории, :К одной мы причислим все те, которые приводятся н непосредственному исследованию возмущенного цвиженин, и в основании когорых поэтому лежит рааысканив общих или частных решений дифференциальных уравнений ( 1). Вообще эти решения придется искать под видом бесконечных рядов, простейшим типом которых могут служить рассмотренные в предыдущем параграфе. Это суть ряды, расположенные по целым положительным степеням постоянных произвольных. Но далее мы встретимся также и с некоторыми рядами другого характера. Совокупность всех способов исследования усгойчивости, относящихся н этой категории, назовем первою методой. Н другой мы причислим все те, которые основываются на принципах, нс зависящих от разыскания каких-либо решений дифференциальных уравнений возмущенного движения.

А. м: ЛЯПУНОВ

ОБЩАЯ ЗАДАЧА ОБ УСТОИЧИВОСТИ ДВИЖЕНИЯ 37

для веяного t, большего некоторого предела t₀или! равного ему. Будем: притом рассматривать только такие функции, для модулей которых при изменении t от t₀до какого угодно данного числа Т, большего t₀, суще ствовали бы высшие пределы. Всякую такую функцию будем пааывать ограничен ною, если модули ее при: t > t₀остаются всегда меньше некоторого предела. Напротив, функцию, модули когорой надлежащим выбором значений t, больших t₀, могут быть сделаны большими веяной данной положительной величины, как бы она ни была велика, будем называгь неограниченною. Наконец, ограниченную функцию, когорая с беспредельным возрастанием t приближается к пределу, равному нулю, будем называть исчезающею. Рассматривая одновременно с функцией х функ 1 цию - , будем предполагать, что при веяном данном Т, х большем t₀, в промежутке от t₀до Т точный низший предел модуля функции х отличен от нуля. Л е м м а I. Если. х есть ограниченная функция t, то хе-лt при всяком положительном постоянном л. есть функция исчезающая. Лемма непосредственно вытекает из предыдущих u определении. Л ем м а II. Если х не есть исчегающая функци.r~ t, о хе" при всяком положительном постоянном л. есть функция неограниченная. В самом деле, если х не есть исчезающая функция, по всегда найдется такая положительная постоянная а" ри которой надлежащим выбором значений t, больших роизвольно заданного предела Т, нак бы он велик ни ыл, модуль функции х можно будет сделать превосходящим а. Тогда, рассматривая только выбранные аким образом значения t, будем иметь: 1 хе" 1 > аелт. А этим и доказывается лемма, ибо вторую часть неравенства выбором достаточно большого Т можно сделать сколько угодно большою.

А. яглнптнов

- таких, чтобы каждое число первого ряда было менее каждого числа второго, чтобы разность л(n) - 1,п выбором достаточно большого п можно было сделать насколько угодно малою и чтобы функция хелпt для всякого п была исчезающею, а функция xeл(n)t для всяRого п неограниченною.

ОБЩАЯ ЗАДАЧА ОБ УСТОИЧИВОСТИ ДВИЖЕНИЯ; 39: Эти два ряда определят число л₀, не меньшее ни одного из чисел первого ряда и не большее ни одного из чисел второго, которое и будет искомым. Число л₀будем называть хар антериотичным числом функции х. Примечание. Функция х, для которой произведение хе" есть исчезающая функция при веяном л или неограниченная при веяном л, не имеет характериствчного числа. Но мы можем условиться говорить, что в первом случае характеристичное число есть + се, во втором - со. При этом условии веяная функция будет иметь конечное или бесконечное харантеристичнов число. Приведем примеры. Для веяной отличной от нуля постоянной ха рантеристичное число есть нуль, а для нуля + со . Для функции tm (т-постолнная) харантеристичное число равно О. 1 t соs- Для функции е t харакгервстичное число равно - 1,

+ 1,

e±t sin t

e-tesin t


		-tcos-				+ 1,
»	»	е t	»	»	))	+ 1,
»	»	e±t sin t	»	»	»	-1
»	»	e±t sin t	»	»	»	'
»	>>	etesin t	»	»	»	-е,
»	»	e-tesin t	»	»	»	-!- _!_
»	»	e-tesin t	»	»	»	, е ,
»	»	ti	»	»	»	-ос,
»	»	с:'	»	»	»	+ оо ,

надлежащим выбором значений t, больших произвольно заданного предела, можно сделать наскольно ~ГО,Ц:ЦQ м~лою, и есл~ притом для UСЯJ{ОГО UQЛOiRП-

Примечание. Вообще если f(t) есть такая вещественная функция t, а 1 ... такая вещественная постоянная, нто величину

о

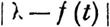
тельного постоянного г, как бы оно мало ни было, ожно найти такой предел Т, что л-/(t)<г ля всех значений t, больших Т, то ) .. есть характеристичное число функции ·e-tf(t) •

будут исчезающими для веяного отрицательного г. Такою же будет поэтому и сумма их. Если же притом л₁< ).._₂, то при

первая из этих функций будет неограниченною, вторая исчезающею, а следовательно, сумма их неограниченною. Но тогда последняя будет неограниченною. и для всякого положительного а. Поэтому харантеристичное число функции х₁+ х₂, будучи во веяном случае не менее л₁, при последнем условии равно 1"₁• Примечание. Ногца слагаемые функции, имеющие авные харантеристичные числа, таковы, что отношв-

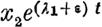
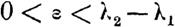
ОБЩАЯ ЗАДАЧА ОБ УСТОЙЧИВОСТИ ДВИЖЕНИЯ

ние их есть величина чисто мпимая или вообще номплекснан с постоянным аргументом, отличным от не- u четнои кратности те, то характеристичное число суммь: всегда равно харакгеристичному числу слагаемых. Лемма V. Характеристичное число п роизведения двух функций пе менее суммы их характеристичны чисел. В самом деле, если л₁и л₂суть характеристичные числа функций х₁и х~Р то функция

Х1 Х2е(А1 +А2+•) t = Х1е (л1-t-;) 1 Х /А2+½) / 2

есть исчезающая для всякого отрицательного в. Что харантеристичное число произведения може быть более суммы харантеристичных чисел произво u дителеи, достаточно ясно видно из приведенных выш примеров. Следствие. Сумма характеристичных чисел функ ...             1     б циц х и - не олее нуля. х Ле~1ма VI. Если

х = е:" (/+if), где i ==- V -1, а f и ер суть некоторые вещественные функции t, то для того, чтобы сумма характеристич- пых чисел фуnК,цuй х и .!.. была равною пулю необ- х одимо и достаточно, чтобы фупкция f с б есп редель ным воэрастанием t приближалась 1i, некотором пределу. Достаточность скааанного условия очевидна, иб если функция / с беспредельным возрастанием t стре ится н некоторому пределу, то последний служи арактеристичвым числом функции х. Что же касается его необходимости, то она следуе из того, что если ), и - ; .. суть характеристичвые числ              u            1 уннцnи х и - , то при веяном дaH:JIOM полощ~тел~

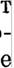
как бы оно мало ни было, обе функции е:' (е.-л+f) и е=! (s.+л-/) L_удут исчезающими; а последнее возможно только при l)'СЛОВИИ, ЧТО lл-/l<e

u наидем

S>л+(J,, fl->S-л,

откуда

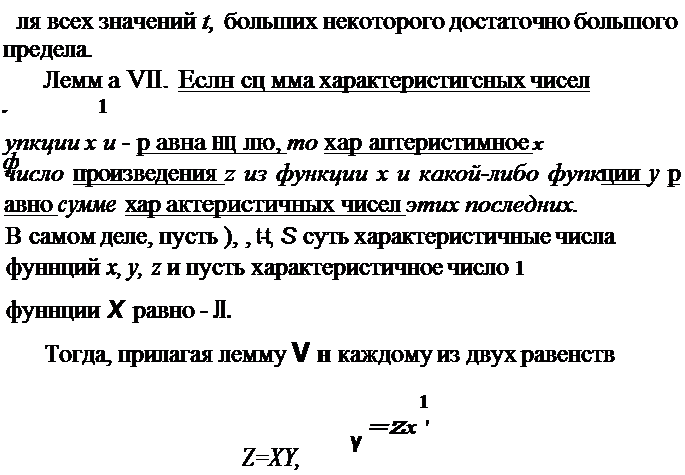Пусть х есть интегрирующаяся функция t. Означая через t₁какое-либо не меньшее t₀дан вое число, рассмотрим интеграл

если хара:ктеристичное число фуннции х отрицательн

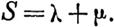
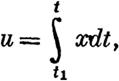
ОБЩАЯ ЗАДАЧА ОБ УСТОЙЧИВОСТИ ДВИЖЕНИЯ

или равно нулю, и интеграл

и=~ xdt, t

если это характеристичное число положительно. Тогда докажется следующее предложение. Лемм:а VIII. Характеристичное число интег_рала не менее харантеристичного числа подинтее рольной функции. Пусть ), есть харантеристичное число фупкциих. Тогда функция

при веяной положительной постоянной ~ будет исчезающею и, следовательно, ограниченною. Означим через М высший предел ее 1\tодулей для t > t₀• При: л > О и ~ < ),. будем иметь

ие<л -Е> t

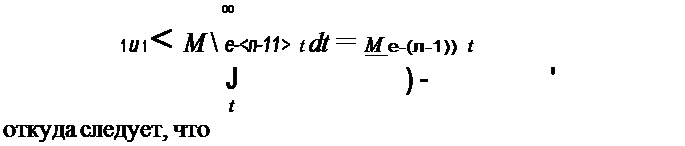есть исчезающая функция при всяком г, большем 'fl. Но ~ можно предполагать насколько угодно малым. Поэтому предыдущая функция есть исчезающая пр веяном положительном г. При А. ,< О будем иметь t 1 и 1 < М ~ е-<А-1)) ¹dt = __ м, e-<A-YJ)' + const., t1

откуда следует, что

(л -Е) t

нов

есть исчезающая фуннция при веяном з, большем ~' а, следовательно, и при веяном положптельном г. Далее нам придется рассматривать группы, состо- щие из неснольких фувкций. При этом мы введем понятие о характеристичном числе группы, называя так наименьшее из харакгервсгичных чисел функций, составляюгцих группу. 7. Характеристичные числа решений линейных дифференциальных уравнений.Рассмотрим систему линейных дифференциальных уравнений: ~· = Р₅1Х1 + Ps2X2 + · . · + PsnXn (s = 1, 2,... , п),( 15)

предполагая, что все коэффициенты р яв определенным образом заданы по крайней мере для всех значений t, не меньших некоторого предела t₀, и представляют непрерывные и ограниченные вещественные функции t. Говоря о наком-либо решении этой системы уравнений, будем подразумевать, что речь идет о группе п функций

совокупно удовлетворяющих этим уравнениям (а еле довательно, определенных и непрерывных) привсяком~.t, не меньшем t₀• 'Гакие группы функций, как уже было замечено раньше, всегда могут быть найдены. Притом V всегда наидется п таких групп, которые составят u систему п независимых решении. Те о рем а I. Всякое решение системы дифференциальных уравнений (15), отличное от очевидного

име: т конечное характеристичное число [⁵]. Будем рассматривать только решения, в которых не все функции Х₅тождественно равны нулю. При это сначала рассмотрим решения вещественные, т. е. такие, в которых все xS_ суть вещественные функции t.

ия

Разумея под ), некоторую вещественную постояную, положим:

(s==1, 2, ... , п).

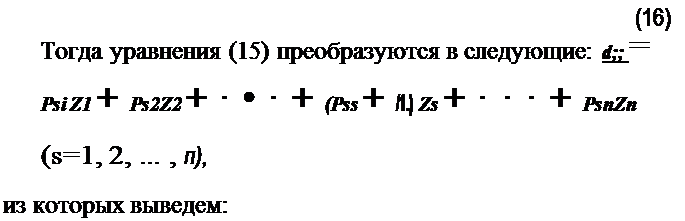п : 1е ~ z; = ~ (Pss + ),) z; + ~ (Pso + P,s) Z₅Zo,                                   S= 1                 S =1

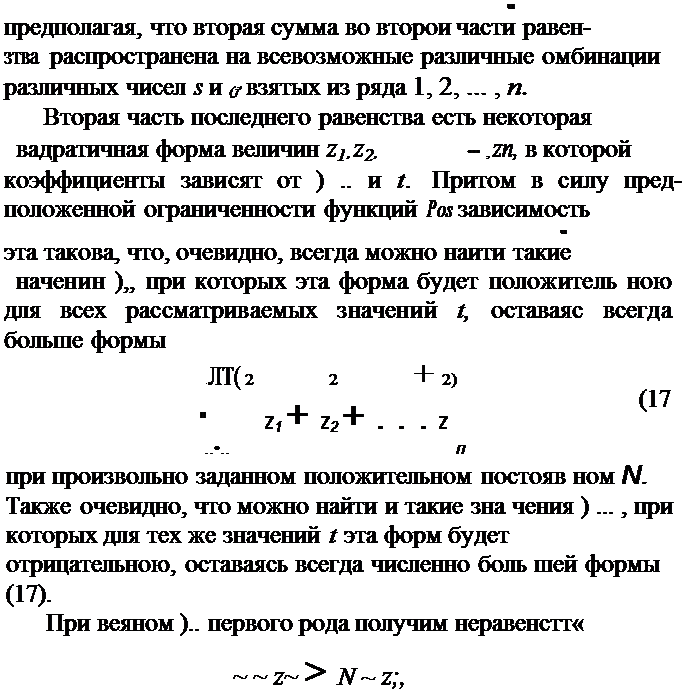⇐ Предыдущая 1 234 5 6 7 8 Следующая ⇒