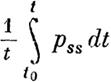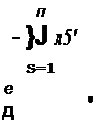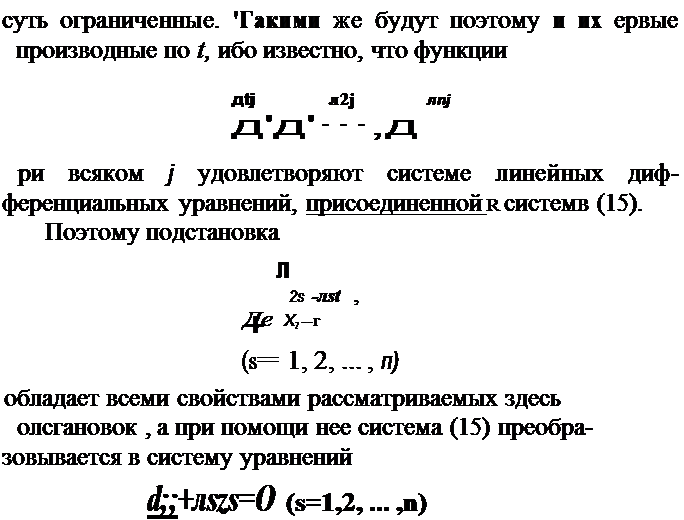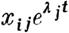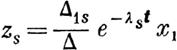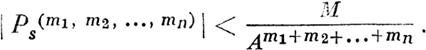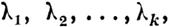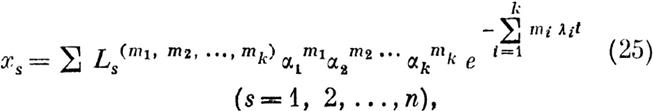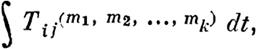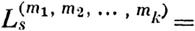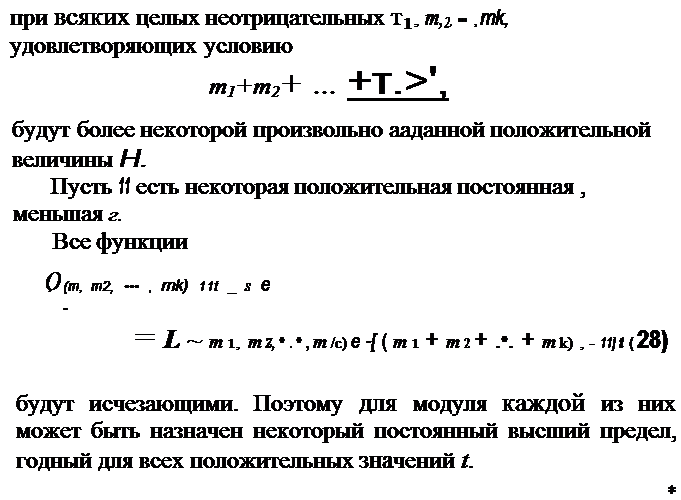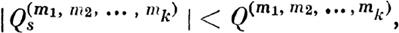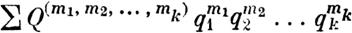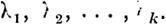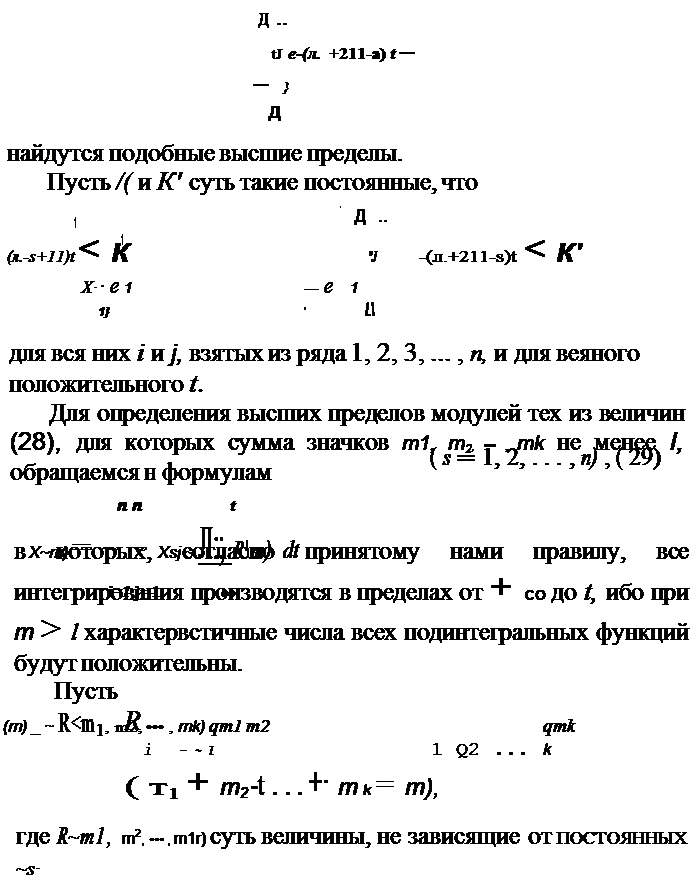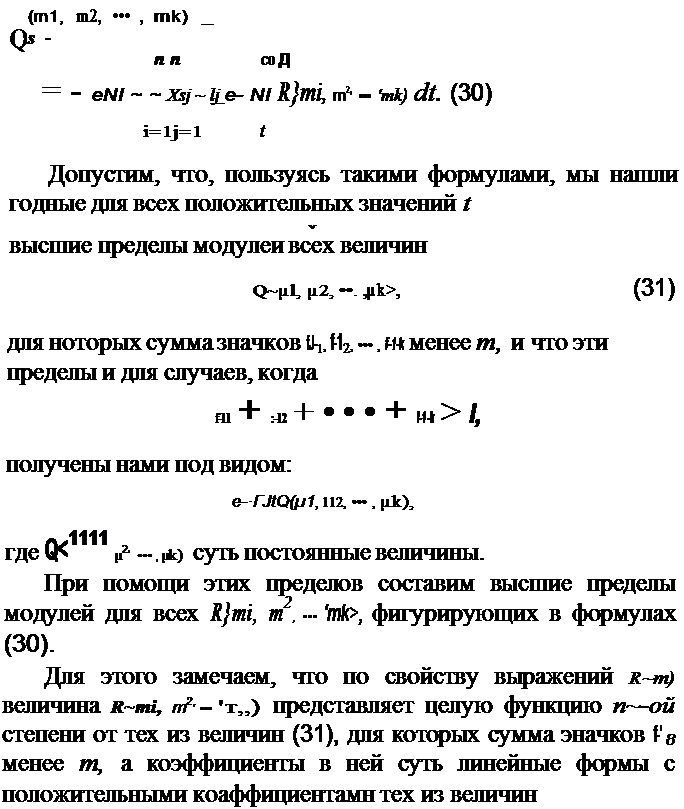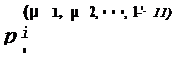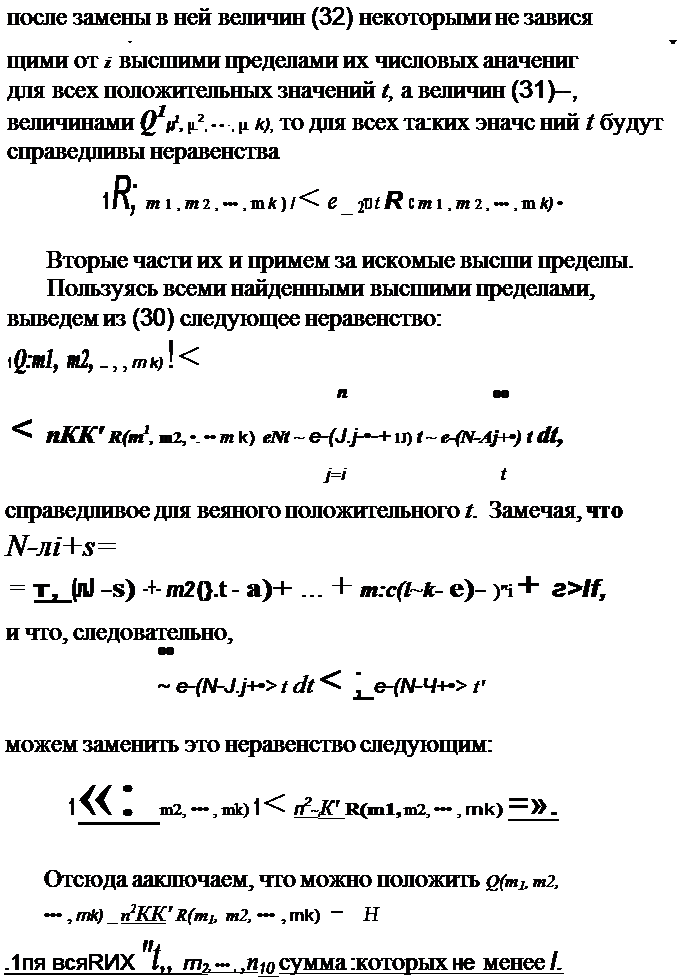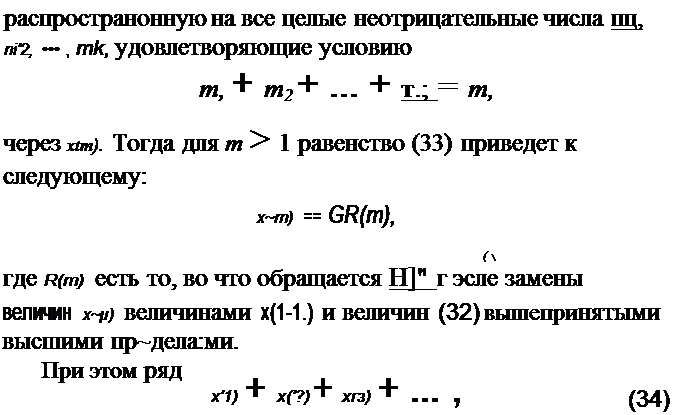Рнь>: У. 5 страница

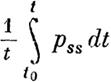
Таким образом веяной системе п линейных дифференпиалъных уравнений рассматриваемого вида будет соответствовать группа п характеристичных чисел, между которыми могут быть и равные. Пусть система уравнений ( 15) преобразовывается при помощи линейной подстановки zs == qs1X1 + qs2X2 + • · · + qsnXn (s= 1, 2,· • •, n), обладающей следующими свойствами: все коэффициенты q s<J суть непрерывные и ограниченные функции t, ихпервые производные суть функции такого же характера, и величина, обратная составленному из этих коэффициентов определителю, есть ограниченная функция t. Притаком преобразовании коэффициенты в преобразованных уравнениях будут обладать теми же основными свойствами, что и в первоначальных. Нетрудно доказать, что группа характеристичных чисел преобразованной системы уравнений всегда будет тождественной с группою характеристичных чисел пе реоначаяъной, В самом деле, по свойству рассматриваемой подстановки не только ее коаффициепты, но и коаффициенты обратной подстановки суть ограниченные функции t. Поэтому, если при посредстве соотношений между функциями х и функциями z из какого-либо U V решения однои системы уравнении выведем решение

другой, то оба эти решения будут обладать одним и тем же характеристичным числом. А отсюда (в силу понятия о нормальной системе решений) следует, чта всякое число, встречающееся известное число раз в группе характеристичных чисел одной системы уравнений, необходимо встретится такое же число раз и в группе характеристичных чисел другой. Таким образом характеристичные числа системы инейных дифференциальных уравнений по отношению R рассматриваемым преобразованиям обладают свойствами инвариантов. Теми же свойствами по отношеию к этим преобразованиям обладают и характеристичные числа функций ef ~JJs~dt и e-f ~Pssdt.

. . . . . . . . .

Х1п, Х2п, • • ·, Хп.п

В--ИШЕНИЯ

U V есть наидецная для нее нормальная система решении, в которой j-oe решение обладает характеристичным числом ) ... j. Означая через ~ определитель, составленный из функций Xij, допустим, что все функции

(i, j===1,2, ... ,n)

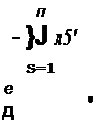суть ограниченные. Можно показать, что при этом условии система ~уравнений (15) есть приводимая. В самом деле, означая минор определителя Л, соответствующий элементу xu, через Ли, из предыдущего условия выводим, что все функции

до е _,. jt д

(i,j=1,2, ... ,n)

С П<1СТОЛННЫМИКОЭ

ициентами.

~rvr. ЛЯПУНОБ

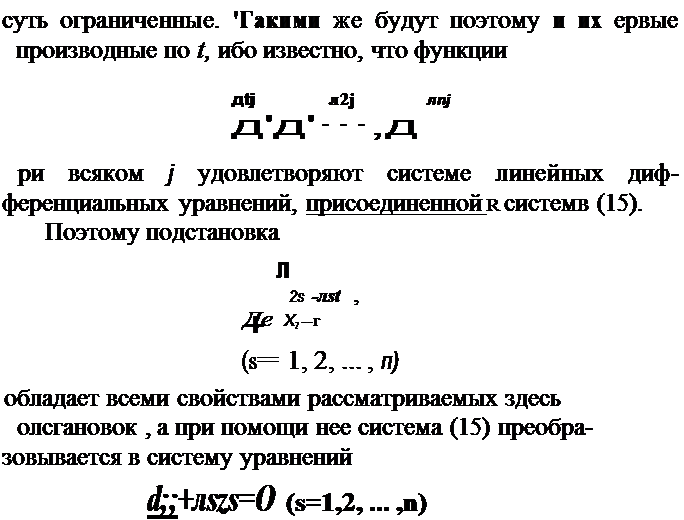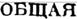
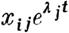
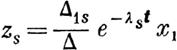
О НЕКОТОРОМ ОБЩЕМ СЛУЧАЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИ11 ВОЗМУЩЕННОГО движвнин 11. Определение некоторого нового типа рядов, расположенных по степеням постоянпых произвольных.Обращаемся теперь н уравнениям (1). Рассматривая попрежнему только вещественные значении t, не меньшие некоторого предела t₀, будем предполагать в этих уравненилх все коэффициенты Psa, ps·m1, т2, ... , тп) непрерывными и ограниченными вещественными функциями t. Притом будем предполагать, что могут быть найдены такие положительные постоянные М и А, при которых для рассматриваемых а начений t будут справедливы неравенства

Допустим, что система дифференциальных уравнений, соответствующая первому приближению, есть правильная и что Л 1' Л 2' • • . , /, n суть характеристичные числа этой системы. Мы покажем, что, выбирал из этих чисел какиел ибо k (24) можно составить формально удовлетворяющие уравнениям: (1) и содержащие k постоянных проиввольных

r:l.i' ~2'• • • ' r:J.k

ряды следующего вида:

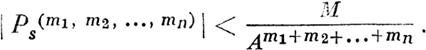
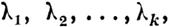
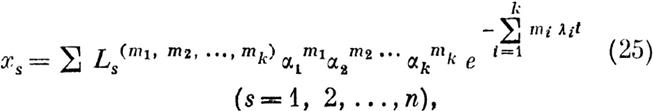
ОБЩАЯ 3АДАЧА ОБ УСТОЙЧИВОСТИ движвния

где L/m1, т2, ···, mk: суть не зависящие от постоянных ai непрерывные функции t, характеристичпые числа которых не менее нуля, причем суммирование распространяется на все целые неотрицательные значения чисел ni₁, ni₂, ••• , mk, подчиненные yc;ronиro т₁+- т₂+ ... + т1с > О. Мы будем затем исключительно рассматривать тот случай, когда выбранные характеристичные числа (24) все положительны, и в этом предположении покажем что при всяких о:₁, cr.₂, ••• , (/.k, модули которых не превосходят некоторого предела, ряды (25) будут абсолютно сходящимися и представят функции, действительно ~довлетворл1ощие уравнениям (1) для всех значений t превосходящих t₀• Обращаемся н формулам § 3. Допустим, что система частных решений уравнений (6), которою мы там пользовались, есть нормальная п что решение

обладает характеристичным числом лs (s-::::-: 1, 2, ... , п). Полагаем (s==1, 2, ... ,п).

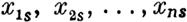
постоянных под видом целых однородных функций V п~-ои степени. Пусть

л.. ~ ( r J R, т ) Т rn 1 , m 2 , ••• , т ,'.) ,., т 1 ,., m J 1У т k Д i =-= ij ~ \А,1 \А,1 •• • .,,..k '

где Т суть функции t, не зависящие от постоянных rJ.₅• Тогда, делая

п п х~т) = ~ ~ X₈j ~ ~i R~m) dt, i=1j=1 \ длii R\m)dt. = ~ а.т1 ат2 ..• amk fTi1.rm.1, т2, ••• , mk) dt, ~ l 1 2 k )

каждый из интегралов

в котором поби.нтеераяъная фун-,;,цил обладает положительным характеристичным числом, будем брать в пределах от + со до t. Что же касается тех, для когорых характеристичные числа подинтегральных функций отрицательны или нули, то, вообще делая ~ T}i1, m2,••. ' mk) dt = t = ~ T}i1, m2,..• , mk)dt + C~jl• m2,•.• , mk>, to

будем только предполагать, что постоянным С приписываются накие-либо не зависящие от постоянных as определенные значения. Рассматриваемые интегралы будут при этом обладать характеристичными числами, не меньшими характеристичных чисел соответствующих поцинтегральных функций (лемма VIII).

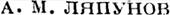
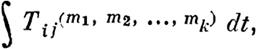
Желая придать им вид (25), мы лолжны будем сделать:

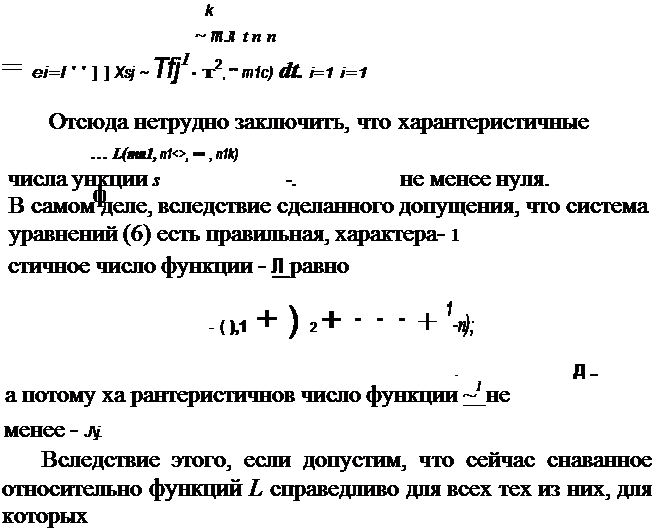то по свойству величин R~m) ааключим (леммы IV, V), что характеристичное число функции T}j¹' т², ••• , mk), для которой

5 А. М. Ляп_rнов

бб

А. :м. ляпънов

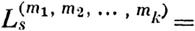
а следовательно, и характеристичное число интеграла ~ тf Т" щ2, ••• ' m k) dt

не менее

Отсюда же выведем, что характеристичное число всякой функции L, для которой сумма значков m i равна 1n, не менее нуJ1я. Поэтому рассматриваеl\1ое свойство функций l;, будучи справедливым в случае ~ mi =-: 1,справедливо вообще. Примечание. Чтобы пригти н таному результату, очевидно нет надобности при составлении рядов (25) интегрировать в пределах от + со до t непременно каждую из функций T{j¹' тз,.,.' т,) с положительным харантеристичным числом. Достаточно интегрировать н таких пределах только те из них, для которых т1л1 + т2)·2 + · · · + mkл.k-) j > О. 12. Теорема о сходимости рядов.Переходя теперь н вопросу о сходимости рядов (25), будем предполагать, что все взятые для составления их характеристичные числа (24) положительны. При этом лля упрощения игследопания примем l₀== О. Тогда цокажется следующее предложение. Т е о р е м а. Если, разумея под s некоторцю положитмъную . постоянную, сделаем

ase-(лs-s) t = qs

( s = 1, 2, ... , k)

и величины ГJ.₈в рядах (25) заменим следующими отсюда их выр ажениями, то получим новые ряды

_ ~ Q(m₁, n:2, ••• , mk) m1qm~ qmk Xs - ~ s q1 'l · • • k (s == 1, 2, ... , п),

(26)

ОБЩАЯ ~АДАЧАОБ УСТОИЧИВОСТИ ДВИН{ЕНИН расположенные по восходящим степеням величин q ₈, которые будут такого свойства, что при всяком ~, как бы оно мало ни было, найдится такие поло жительные постоя.нные Q:m1, т2, · · · , mk), при которых для всех неотрицательных вначений t будут справедливы нер а- венства

а рлд

(27) будеп~ абсолютно сходящимся, пока моду.ли величин, qs не превосходят некоторого отяичного 01n пуля предела q. Будем рассматривать только такие положительные значения е, которые менее каждого из чисел

Тогда найдется такое целое положительное число l, что все выражения т ₁(), ₁- s) -J- т₂()-. 2 - г) + . . . + mk ( i. k - е) - л j + е (j == 1, 2, ... , п)

6Н

А.М.ЛЯПУНОВ

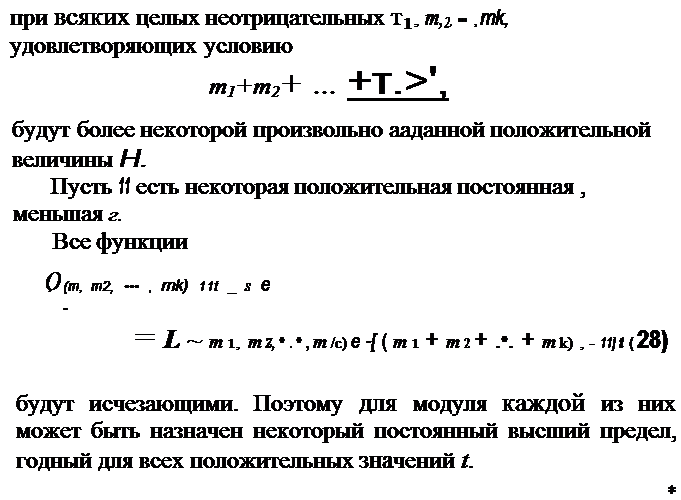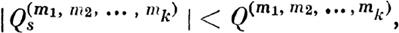
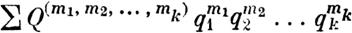
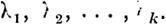
Пусть такие пределы, которые притом предположим не зависящими от s и означим через Q<m1, т2, ···, ¹¹¹1<), V наидены для всех тех из них, для которых т₁+ т₂+ ... + mk < l. Между ними будут между прочим функции (л. - a+·IJ) t Xije 1 • Если же предположим еще JJ > ; , то и для модулей фуннций

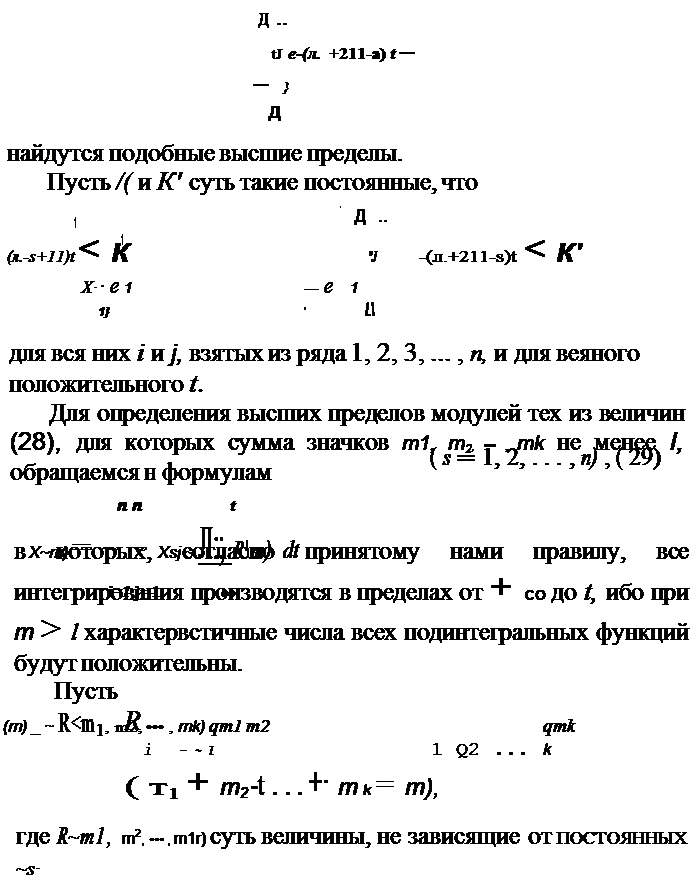ОБЩАЯ ЗАДАЧА ОБ УСТОЙЧИВОСТИ ДВИЖЕНИЯТогда, полагая для сокращения т₁л₁+ т₂1-..₂+ ... + mkл.k- та= N, из (29) выведем:

(32)

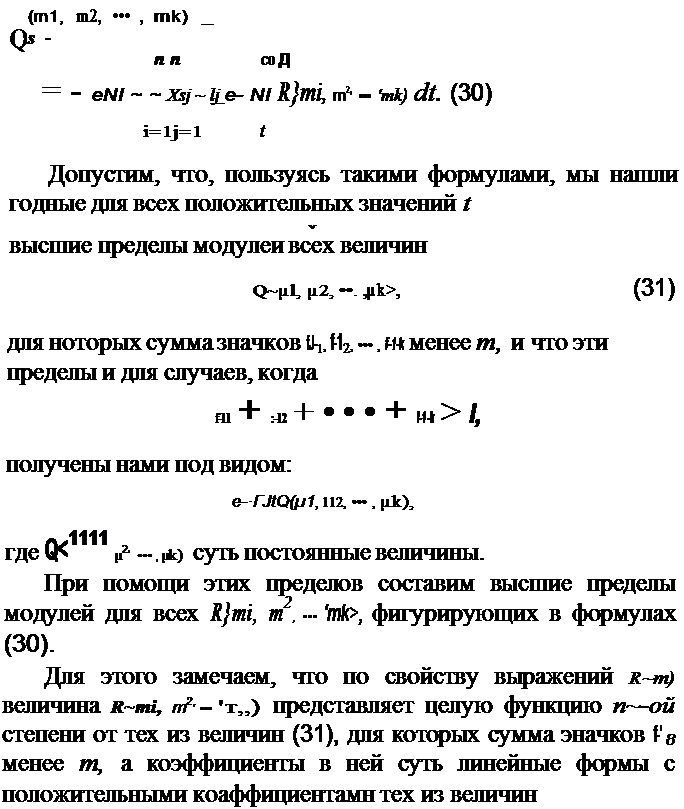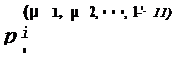для которых сумма значков r ₁, r-~, ... , Р» не более 1п. Притом относительно величин (31) степень каждого члена этой функции не ниже второй.

• ЛЯПУНОВ

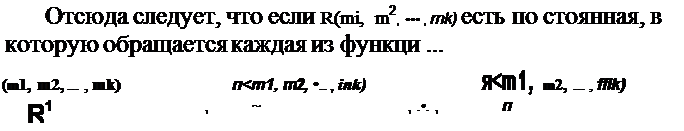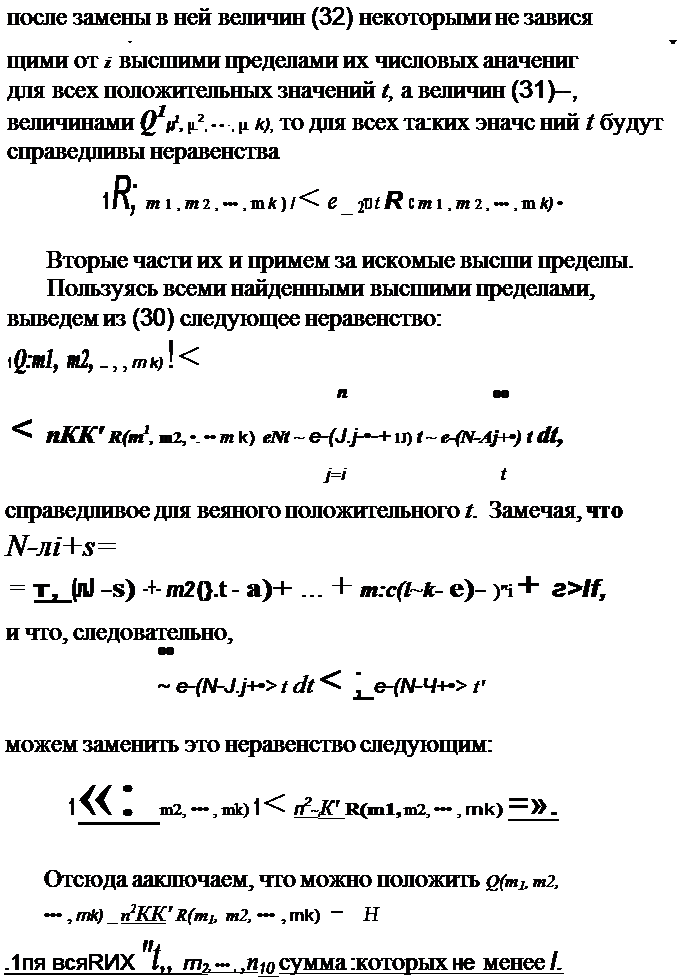ОБЩАЯ 3АдАЧА ОБ }'·стоnчивости ДВИН'\ЕНИЯ

Но, выбирая достаточно большие величины для К и К' или достаточно малую величину для 11, очевидно, можем достигнуть того, что величины Q, определяемые но этой формуле для аначков, удовлетворяющих условию 1 < т₁+ т₂+ ... + mk < l, будут не менее тех, которые мы нашли для них раньше. Поэтому, заменяя последние, если это необходимо, большими величинами и означая через G некоторую достаточно большую положительную постоянную, можем сделать Q(т₁, т1., •••, тk) = GR(ml' ml., ••• , тk) . (33) для вся них т., m₂, ••• , mk, сумма кого рых больше 1. Для тех же, сумма ноторых равна 1, можем положить Q(m1,m2, , •• , mk) == /(.

Оаначим сумму ~Q(m₁,m₂, ••• , тk) q~l q~12 •..q'f:k,

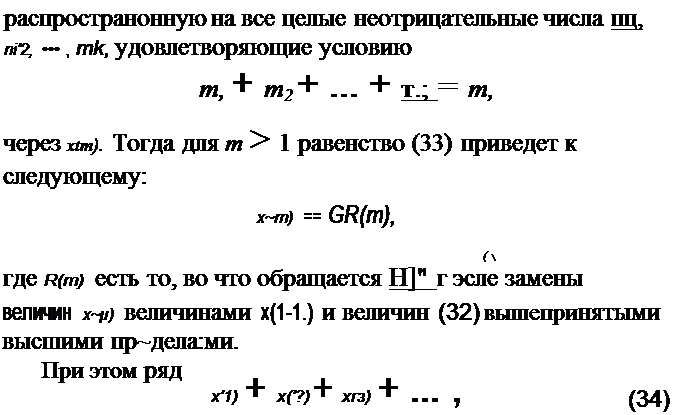., расположенныи по восходящим степеням величин q₈, будет обладать членами, модули :которых более модулей

. ЛЯПУНОВ

соответственных членов каждого из рядов (26) для веяного положительного t (они будут даже более этих модулей, умноженных на е11¹). Но ряд (34) можно рассматривать как расположен- u ныи по восходящим степеням величины ql + q2 + • • • + qk, и если, согласно замеченному в предыдущем параграфе за высший предел числовых значений величин (32) примем следующую ]у]

то ряд этот, по существу, не будет отличаться от того, н исследованию которого привелся вопрос в § 4. Поэтому, если остановимся на такой гипотезе, то наверно найдется такая положительная величина q, что для всяких q₁, q₂, ••• , qk, удовлетворяющих условиям (s===1, 2, ... , k), ряд (34) будет абсолютно сходящимся. Теорема, следовательно, доназана. След ст в и е. Можно найти такую пояо жителънрю постоянную а, что при есяниа а.₁, а.₂, ••• , а.;\, удовлетворяющих усJ1овиям 1 cts\-<~ (s= 1, 2, ... , k), и для всякого неотрицательного t ряды (25) буду,п абсолютно сходящимися, представляя притом неп.реывн ые фу нкц ии t. Что функции эти удовлетворяrот уравнениям ( 1), докажется гак же, на 1, в § 4. Примечание. Если система дифференциальных уравнений первого приближения не есть правильная . то означая через S сумму всех ее характеристичны.>.

⇐ Предыдущая 1 2 3 456 7 8 Следующая ⇒