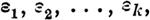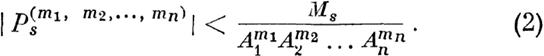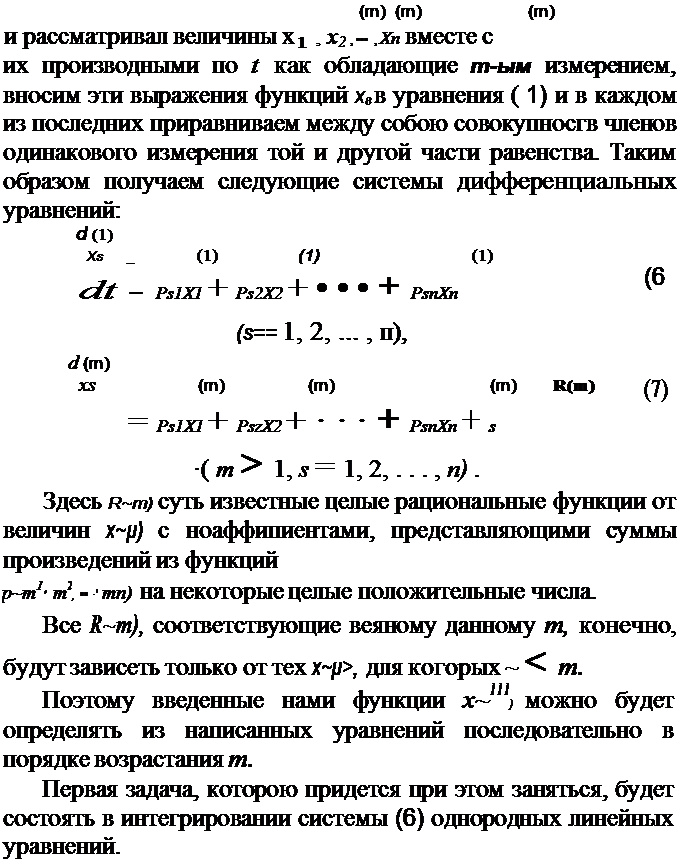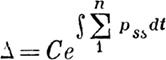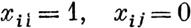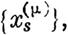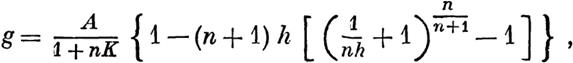Рнь>: У. 2 страница

А.

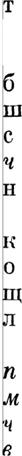
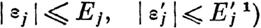
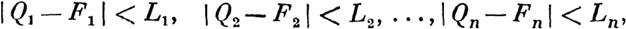
ний, подчиненных некоторым условиям вида: f = о или / >- о, где f - некоторая функция величин

А. :м. ЛЯПУНОВ

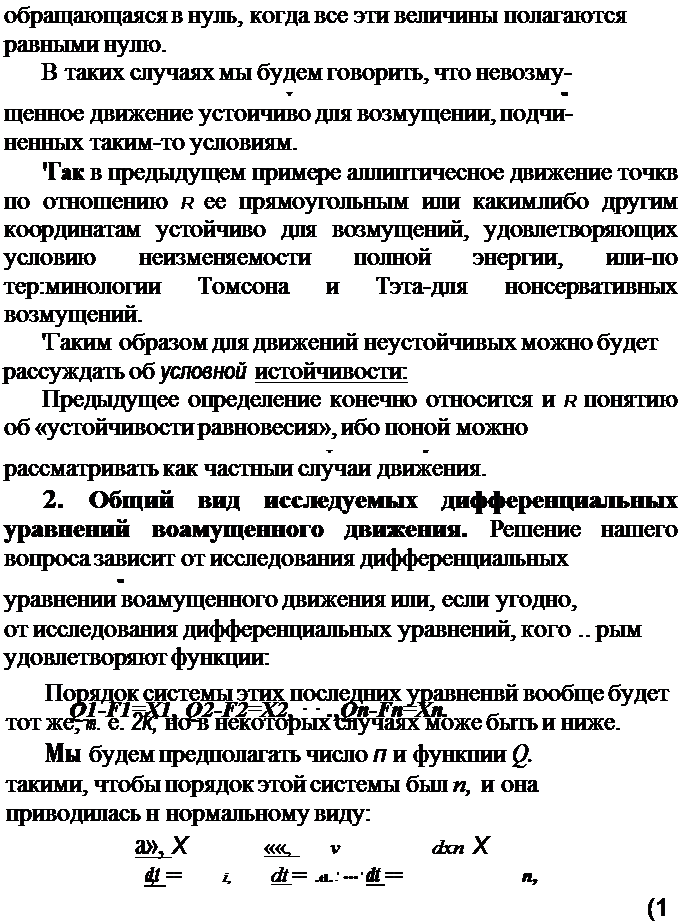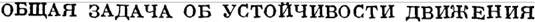
везде далее будем рассуждать об этих последних равнениях, называя их дифференциальными уравнеиями возмущенного движения. Все Xs в уравнениях (1) суть известные функции еличин

обращающиеся в нуль при х₁== х~ == .•. == хп == О.

Мы сделаем теперь относительно них некоторые предположения, и везде далее будем трактоватъ ураnнения (1) исключигельно в этих предположениях. Мы допустим, что функции Х; даны не только для вещественных, но и для комплексных значений вели- ин х₁, х₂, ••• , хп, модули которых достаточно малы, и что по крайней мере для веяного вещественного t, большего или равного t₀, функции эти равложимы в ряды по целым положительным степеням величин ~₁, х;!, ... , хп, абсолютно сходящиеся для всяких Х₈, довлетворнющих условиям 1 Х1 \ < А1, 1 Х2 \ < А2, · · ·, \ Хп \ < Ап, где А₁, А₂, ••• , Ап суть или отличные от нуля постоянные, или такие функции t, ноторые никогда не делаются нулями, Таним образом для веяного из укааанных значений t все Xs будут голоморфными фуннцпями величин х₁, 2, • • • , х1/) ·

.¹) Употребляя этот термин для сокращения речи и везде далее, считаем нужным сказать определенно, что мы будем разуметь под ним. Рассматривая какую-либо функцию переменных х₁,х₁₂, ••• , хп, мы будем называть ее по отношению к этим переменным голоморфною веяний раз, когда она может быть представляема под видом п-:кратного ряда, расположенного по целым положительным степеням величин xs, по крайней мере длЧ, всех таких значений последних, .модули которых не п ревосхоlдят некоторых отличных от ниля пределов.

ОБЩАЯ ЗАДАЧА ОБ УСТОЙЧИВОСТИ движвния

Пусть Xs = Ps1X1 + Ps2X2 + · · · + Psnxn + + ~ р(т1, т2, ••• , тп)хт_{1 1}х~₂••• хтп s ~ п'

где сумма распространена на все целые неотрицательные числа т1, m?, ... , rпп, удовлетворяющие условию т₁+ m₂+ ... + тп > 1.

(т т т ) В этих рааложениях все коэффициеиты Ps~, Р s i, ²' ···, п суть функции t, которые, согласно нашему предположению, должны оставаться определенными, а по характеру самой задачи-вещественными для веяного вещественного t, большего или равного tn. Мы будем предполагать кроме того, что для всех таких значений это суть функции непрерывные. Приписывая t какое-либо из указанных сейчас значений и рассматривая в разложении Xs совокупностъ \ . членов выше первого измеревия при всевозможных комплексных значениях величин х₁, х₂, ••• , Хп, модули ноторых соответственно равны А₁, А₂, ••• , Ап, обозначим через М₅некоторый высший предел ее модуля при этих условиях. Тогда по известной теореме будем иметь:

Вообще далее будем рассматривать только вещественные значения t, не меньшие t₀• Если же в какихлибо случаях представится надобность рассматривать ·и другие значения t, то об этом всегда будем упоминать определенно. Заметим, что если вместо времени за независимую переменную примем какую-либо непрерывную вещественную функцию времени, вместе с ним беспредельно возрастающую, то последняя при решении вопроса об устойчивости может играть такую же роль, как JI время. Поэтому независимая переменная t в уравне-

А.М.ЛЯПУНОВ

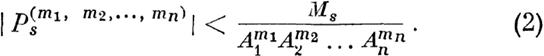
ниях (1) не всегда будет означать время, но во веяном случае-фуннцию его, удовлетворяющую только что сназанному условию, Сделаем еще следующее замечание: Пусть а₁, а₂, ••• , ап суть значения функций х₁, х₂, ••• , хп при t = t₀• Тогда, по свойству функций Q , веяной u системе вещественных значении величин

г1' г 2' ••• ' г k'

(3)

пвсленво достаточно малых, будет соответствовать некоторая система вещественных значений величин

(4)

Притом, как бы ни было мало данное положительное число А, эти последние всегда можно будет сделать численно меньшими А, подчиняя величины (3) условию, чтобы их числовые значения не превосходили достаточно малого, но отличного от нуля предела Е. Мыпредположим теперь, что, как бы ни было мало данное положительное число Е, всегда можно найти такое положительное число А, чтобы веяной системе вещественных значений величин (4), численно меньших А, соответствовали одна или несколъко систем вещественных значений величин (3), численно меньших Е. При этом условии величины ( 4) могут играть такую же роль при решении вопроса об устойчивости, как и величины (3), если только заданием величин (4) функции Х₈, удовлетворяющие уравнениям (1), определяются вполне. Это последнее условие в силу пред- v положении, которые мы делаем далее относительно урав- нений ( 1) (§ 4) всегда будет выполняться. Поэтому далее вместо величин (3) будем рассматривать всегда величины ( 4). . 3. Интегрирование посредством рядов, расположенных по степеням поетовниых произвольных.Для интегрирования уравнений (1) в занимающем нас вопросе естественно представляется метода последова-

ОБЩАЯ ЗАДАЧА ОБ УСТОПЧИВОСТИ ДВИЖЕНИЯ

тельных приближений, основанная на допущении, что начальные ( т. е. соответствующие t == t₀) значения искомых функций численно достаточно малы. Метода эта в своем простейшем виде приводит к ряда:м, которые могут быть получены следующим образом. Полагал

(1) (2) ( 3) 1 2 ) х s == х s + х s + х s + . . . ( s =· ' ' . • . ' п

(5)

А.М.ЛЯПУНОВ

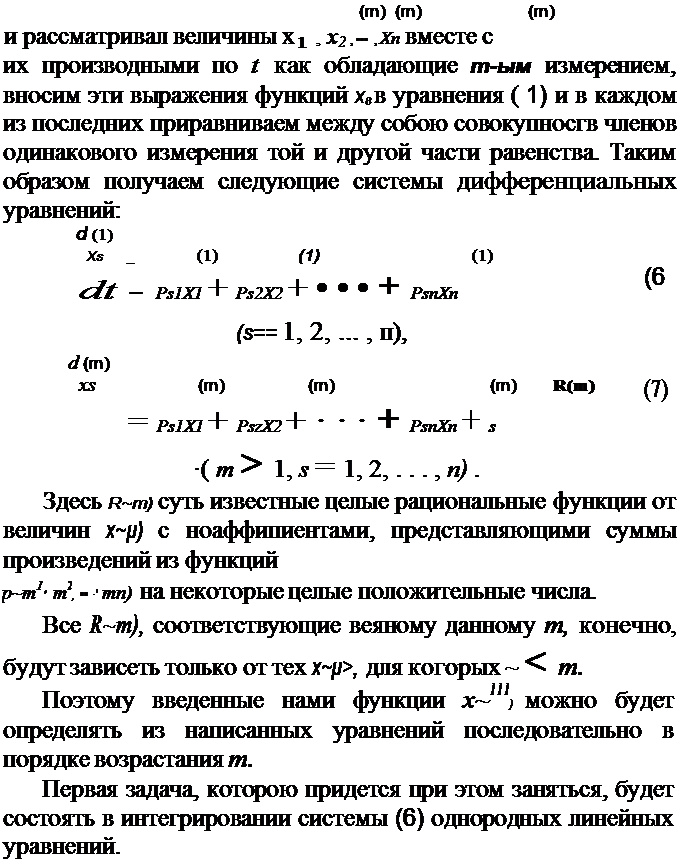¹) Говоря о значениях t, мы всегда имеем в виду некоторые определенные числа. Поэтому бесконечность никогда н~ рассматриваем: как аначение f.

27После того как функции х~⁰найдены, можно будет определять и все остальные х~т) последовательным инте- v рированием систем линеиных неоднородных уравне- ний (7), соответствующих т = 2, 3 ... Каждое из этих интегрирований выполнится при помощи нвадратур. При этом каждое из них введет п постоянных произвольных, и для определения последних представится широний выбор закопа, который вообще должен быть подчинен только условию, чтобы V V случаемые ряды по краинеи мере в известных пределах были сходящимися. Названные постоянные определятся вполне, если введем условие, чтобы все x~m>, для которых т > 1, обращались в нуль при t = t₀• Составим в этом предположении формулы для опре- деления функций х~т>, когда все х~µ>, для которых }1- < т, уже найдены. Положим

Х12

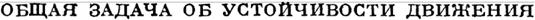
Х11		Х21			. . .		xnl

Х22			. . .		Хп2		1 = л.
.	•	•	.	•	•	.	.	.
Х1п		Х2п			. . .		Хпп

Этот определитель будет функциею t, не обращаю щеюся в нуль ни при каких рассматриваемых нам значениях t, ибо по известной теореме

А. м, ЛЯПУНОВ

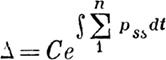
Функции х~т), определяемые этими формулами, остаются определенными и непрерывными для всех рассматриваемых значений t. Относительно постоянных а₁, а₂, ••• , ап это суть целые однородные функции т-ой степени. Притом, если выбранная нами система частных решений уравнений (6) такова, что при t == t₀все xu получают веществеппые значения, то коэффициенты в этих функциях остаются вещественными для всех рассматриваемых значений t. Определив таким образом фуннции х~т>, обращаемся к вопросу о сходимости рядов (5), которые представятся как расположенные по целым положительным степеням постоянных а₈• 4. Исследование сходимости рядов в случае, когда за постоянные произвольные принимаются начальные значения искомых функций, Мыуже сделали некоторые предположения относительно коэффициентов в разложениях вторых частей уравнений ( 1). Теперь прибавим н ним еще одно. Мы будем предполагать, что за величины А₁, А₂, ••• , Ап, М ₁, М ₂, ••• , М п могут быть приняты такие функции t, чтобы для веяного Т, большего t₀, при t, изменяющемся в пределах t₉и Т, для каждой из функций As существовал некоторый положительный низший предел, а для каждой из функций М₈- неноторый высший предел. В этом предположении докажем, что для всех значений t, лежащих между t₀и Т, как бы ни было велико данное число Т., предыдущие ряды (рассматриваемые как расположенные по степеням величин а₈) будут абсолютно сходящимися при всяких 0₈, модули которых не превосходят некоторого отличного от нуля предела, иввестным обрааом зависящего от Т. Докажется это, как и другие подобные теоремы, с которыми встретимся далее, при помощи обычной -р таних случаях методы, ноторою мы обязав:ь1 Romu.

овщхя ЗАДАЧА ОБ УСТОЙЧИВОСТИ ДВИЖЕНИЯ

Обращаясь н этому доказательству, замечаем, чт при t, не выходящем из границ t₀и Т, можно назначит неноторые постояные высшие пределы для модуле л .. lJ V всех Xtj и А или, если угодно, для модулеи всех

Х··-1Х·· Z 1 ' 1 J Д.. Д .. н ₁ l] -- - д ' д

(i ~ j), (i ~ j).

(10 (11

Пусть К есть такой высший предел для величин (10), а К' -для величин (11). Если рассматриваемая система частных решений уравнений (6) определена условием, что при t = t₀ (i ~ j),

то за К и К' можно взять такие непрерывные функции Т, которые будут обращаться в нуль при Т = t₀• Пусть вообще {и} означает результат замены в какойлибо целой функции и от величин а₁, а₂, ••• , ап всех членов их модулями. Тогда, означая через а наибольшую из величин 1 «, \, из (8) и (9) выведем следующие неравенства: {x~i)J < (1 + пК) а, т п т {х~т)} < ~ {Rim)} dt+ (К+ К'+ пКК') ~ ~ {Rim)} dt. to i=1 to Эти неравенства будут справедливы для веяного t, не выходящего из пределов t₀и Т. Замечаем далее, что по свойству первоначального выражения Rim) через вел_ичины х~µ\ Р}т¹,···, тп\ заменяя в нем последние высшими пределами величии

/ p~m1,m2,,,.,mn)I,

найдем высший предел для величины

R(m) l ••

л.М.ЛЯПУНОВ

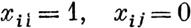
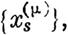
Поэтому, если некоторый общий высший преде величин (µ)} { (µ.)} { (µ)} Х 1 ' Х2 ' •.• ' Хп

{

ОБЩАЯ ЗАДАЧА ОБ ь стоичивости ДВИЖЕНИЯ:

зi

Поэтому, при сделанном выборе величин p(mi, •..• тп>, величина R(m) представит совонупностъ членов т-го измерения относительно аначков величин x:s) в разложении выражения 00 00 М { ( 1- ~ ~ x(s) )-п - 1 - ~ ~ x(s)} • 8=1 8=1 Отсюда следует, что если рассмотрим уравнение х= (1+nK) a+Ah { ( 1-: )-n -1-п:},(12) где h === (1 + пК) (1 + пК') М (Т :-- to) , то ряд х(1) + х(2) + х(в) + ... представит разложение по целым положительным степеням а корня х этого уравнения, обращающегося в нуль при а. О. Поэтому ряд этот будет наверно сходящимся, если а менее величины

u u u представляющеи наименьшии из модулеи всех значе- ний а, при которых уравнение (12) имеет кратные корни. Ряд этот будет сходящимся даже и при а== g, ибо обладает положительными ноэффициентами, а для названного корня, когда а приближается н g, несомненно существует предел. Но по самому определению величин x(m) сходимостью рассматриваемого ряда обусловливается абсолютная сходимость рядов (5) для всех значений t, лежащих между t₀и Т. Поэтому ааключаем.: что для всех таких значений t ряды (5) будут наверно абсолютно сходящимися, если модули постоянных а₈не превосходят величины g.

А.М.ЛЯПУНОВ

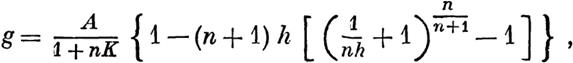
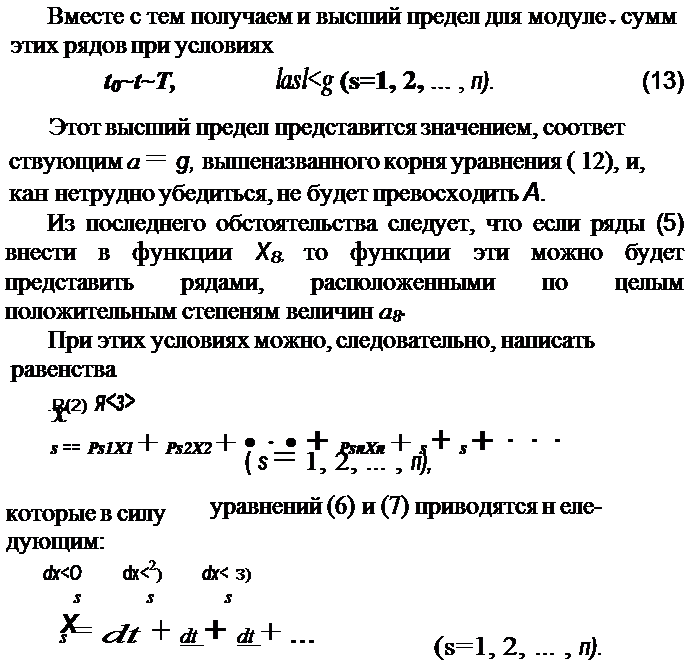Но ряды, находящиеся во вторых частях последних, при рассматриваемых условиях очевидно суть сходящиеся в равной степени для всех значений t, лежащих между t₀и Т, и, следовательно, в этих пределах представляют производные от фуннций, определяемых рядами (5). Поэтому написанные равенства приводят и заклюению, что при условиях (13) ряды (5) представляют функции, действительно удовлетворяющие уравне- ниям (1). . Относительно найденного высшего предела g замеим, что при Т = t₀он принимает значение величины А 1 +пк' оответствующее тому же Т. А значение это, согласно замеченному выше, можно считать равным соответтвующему значению величины А веяний ра~, ногда

⇐ Предыдущая 123 4 5 6 7 8 Следующая ⇒