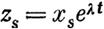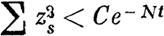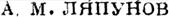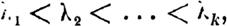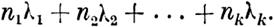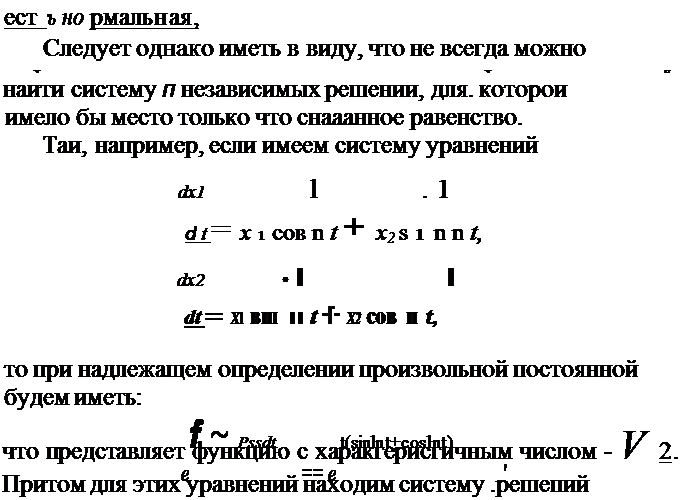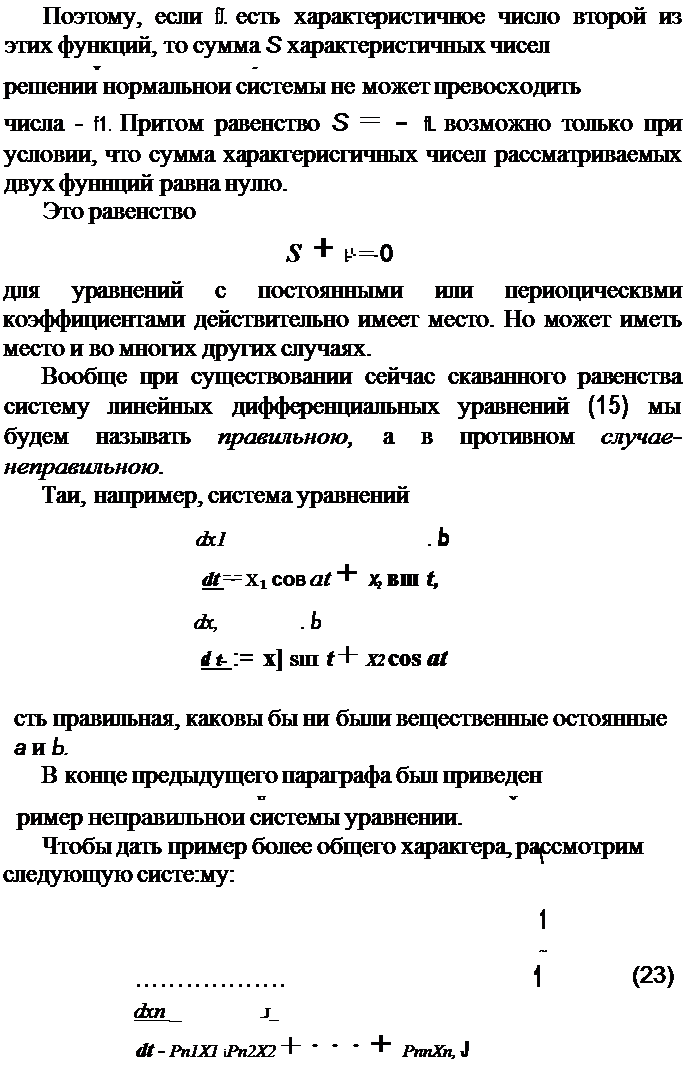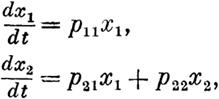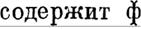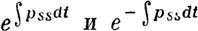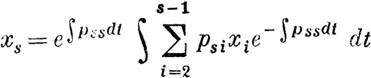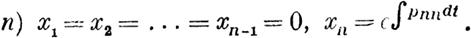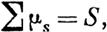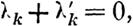Рнь>: У. 4 страница

⇐ ПредыдущаяСтр 4 из 8Следующая ⇒

. м. ляп

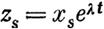
БЩАЯ ЗАДАЧА ОБ УСТОЙЧИВОСТИ ДВИЖЕНИЯ 4? системы уравнений (15) будет составлено из двух веще ственных решений

(20)1

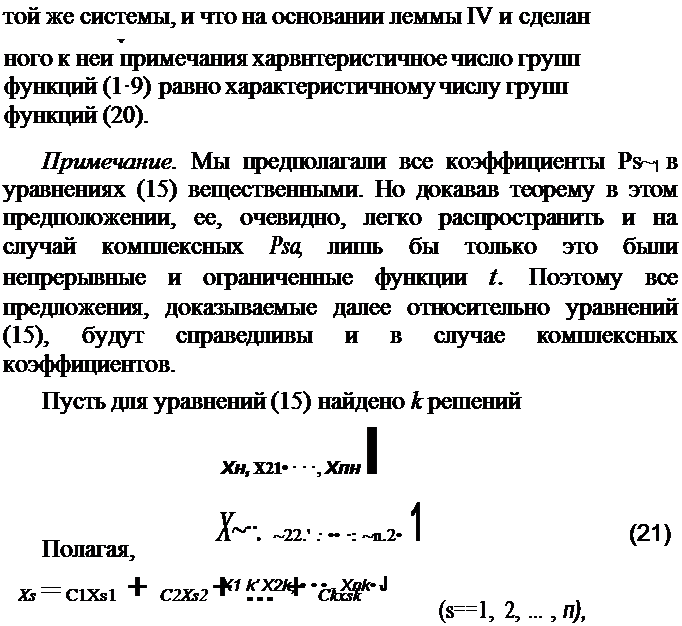где С₁₇С₂, ••• , Ck суть некоторые постоянные, из ноторых ни одна не ни ль, мы будем говорить, что решение

есть яинейная комбинация решений (21). Из леммы IV следует, что характеристичное число решения, представляющего линейную комбинацию V нескольких решении, не менее харантеристичного исла системы комбинируемых решений (т. е. характеристичного числа группы функций, составляющих систему решений) и равно этому числу, :когда харанте-

ристичные числа всех комбивирусмых решений различны. Из последнего выводим, что веяние решения (новечно отличные от х₁== х₂== ••. == хп == О), характеристичные числа которых различны, суть независимые. Отсюда ааключаем о справедливости следующего предложения. Теорем а II. Система уравнений (15) не может иметь больше п решений, отличных от очевидного Х₁=Х₂= ... =Хп==О, характеристичные числа которых были бы все розичными, Везде далее будем рассуждать только о решениях, в которых не все функции х тождественно равны нулю. 8. Нормальные системы решений.Пусть для системы уравнений (15) найдена какая-либо система независимых решений. Составляя из последних всевовможные линейные номбивапви, мы можем вывести из этой системы веяную другую полную систему независимых решений. Допустим, что веяная найденная система п независимых решений преобразовывается в другую по еледуrощему правилу: кажцый раз, когда из каких-либо решений этой системы может быть составлена линейная комбинация, харакгериствчное число которой было б более харвнтеристичвого числа группы комбинируемых решений, одно из последних, а именно одно из тех, арантеристичцые числа которых равны характера- u стичному числу группы, заменяется в рассматриваемои системе этой линейной номбинацией. 'Гак как число различных характерисгичных чисел, которыми могут обладать решения системы уравнений (15), ограниченно, то, поступая таким образом, U V мы получим наконец систему п решении такого свои- ства, что всякая линейная комбинация всяких входящих в ее состав решений будет обладать хар актеристичны числом, раВН,Ы~ ха рактеристичноми числу группы комбинируемых пеаиений .

ОБЩАЯ ЗАДАЧА ОБ ~"СТоИчивости ДВИЖЕНИЯ

Веяную такую систему п решений (которые очевидно независимы) будем называть нормальною, Вследствие предполагаемой нами вещественности коэффициентов PsrJ в уравнениях (15), для уравнений этих можно найти систему п вещественных независимых решений. Исходя из такой системы и при составлении линейных комбинаций пользуясь только вещественнымикоэффициенгами, мы могли бы получить систему п решений, удовлетворяющую предыдущему требованию для всяких линейных комбинаций с вещественными коаффициентами. Но тогда эта система будет удовлетворять этому требованию и для линейных комбинаций с какими угодно коэффициентами (лемма IV, примечание). Система эта будет, следовательно, нормальною. В силу этого замечания мы можем в случае надобности, все функции, входящие в состав нормальной системы, предполагать вещественными. Из определения нормальной системы следует, что u - u если возможно наити систему п решении, характера- сгичные числа которых были бы все различны, то эта система есть нормальная. Из того же определения выводится следующее предложение: Т е о р е м а I. Пу стъ найдена какая-яибо система п независимых решений

Х11,		Х21,			• • •		'	Xn1'
Х12,		Х22,			. . .		'	Хп2,
•	•	•	•	•	•	•	•	•	•
Xin'		Х2п,			. . .		'	Xnn'

Z11' Z21' ••• ' Zni, Z12, Z22, • • • , Zл2,

. . . . . . . . .

(22)

4 А. м. ЛЯПI:ИОВ

п пусть из нее выведена новая

в которой вообще Zsk = Xsk -1-- Ct.k1Xsk+I + r;,k2Xsk+2 + · · · + aJ.;n-kXsn' а f:X1a, a.k₂, ••• , ~J..:n--k сутъта-киепостояпкые,что характеристичное число всякого решения

в котором Xs == Xsk -f- ~JXsk+I + ~2Xs~~2 + · · · + ~n-kXsn' а ~₁, ~₂, ••• , ~п -lc кахие-либо постоянные, не более 'rf;а'рактеристичкого 'Числа решения

суть все эти числа. Оаначим через n₈число решений с характеристичным числом ) .. ₈, входящих н состав вообще какойлибо системы п независимых решений. Некоторые И3 чисел n₅могут быть и нулями. Но они во всяком случае ·будут таковы, что п₁+ п₂+ ... + nk = п. Предполагая

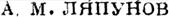
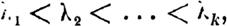
ОБЩАЯ ВАДАЧА ОБ 'УСТОИЧИВОСТИ ДВИЖЕНИЯ 511 означим еще через Ns точный высший предел числа независимых решений с характеристичным числом i"₅, допуснае:мых системою уравнений (15). Очевидно будем иметь: 1V1 > N2 > ... > н; N1=n, ns+ns+i+ ... +nk<Ns (s== 1, 2, ... , k). При этом докажутся следующие предложения: Т е о р е м а IJ. Для всякой нормальной системы решений n₁==n-N₂, n₂=N₂-N₃, ••• ,nk __ ₁=Nk_₁-Nk,nk=Nk. В самом деле, веяное решение есть линейная комбинация некоторых решений нормальной системы. А по свойству этой системы решение, обладающее характеристичным числом л.s, может быть линейною комбинацией только тех решений нормальной системы, харантеристичныо числа которых не менее А₈• Поэтому число допускаемых системой уравнений (15) независи- u ' мых решении с харантеристичным числом J"s не может f ыть более величины ns + ns+1 +- • • • + n10 u u соответствующеи нормальнои системе; а потому для V послвднеи

откуда и следует справедливость теоремы. Теорема III. Сумма ,S = п₁л₁+ п₂1"₂+ ... + n1c1"₁c ~арактеристичпых чисел всех решений, входящих в состав системы п независимых решений, для нормальной системы достигает своего высшего предела. В самом деле, полагая п s -t- ns + ₁+ . . . + п k = N ~,

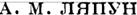
де С - некоторая постоянная. А на основании лемм IV >т V характерисгичпое число д не менее

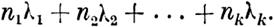
ОБЩАЯ ёАДАЧА ОБ УСТОИЧИВОСТИ пвижвнин

С л е д с т в и е. Всякая система п независимых решений, для которой сум . .ма хар актеристичных чисел всех решений равна характе ристичноми 'Числу фу'нк/цuи. J ~ Pss dt е '

Х1 е' sin ln t '

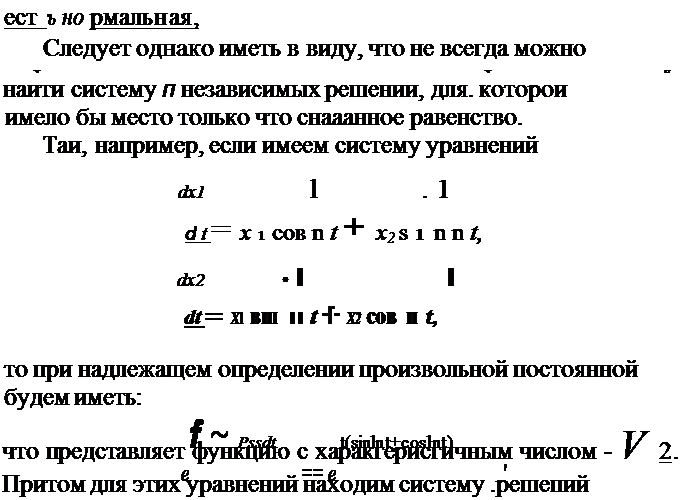Х2 et sin ln t ' _ et cos 111, '

etcoslnt '

которая, кан нетрудно убедиться, есть нормальная, а между тем для нее сумма х аракгеристичных чисел ( равная - 2) менее предыдущего числа. 9. Правильные и неправильные системы уравнений. ¹Мызнаем (лемма V, следствие), что сумма харантеристичных чисел функций

ef ~P s~dt

e-s ~Pss dt

,.. не оолее нуля.

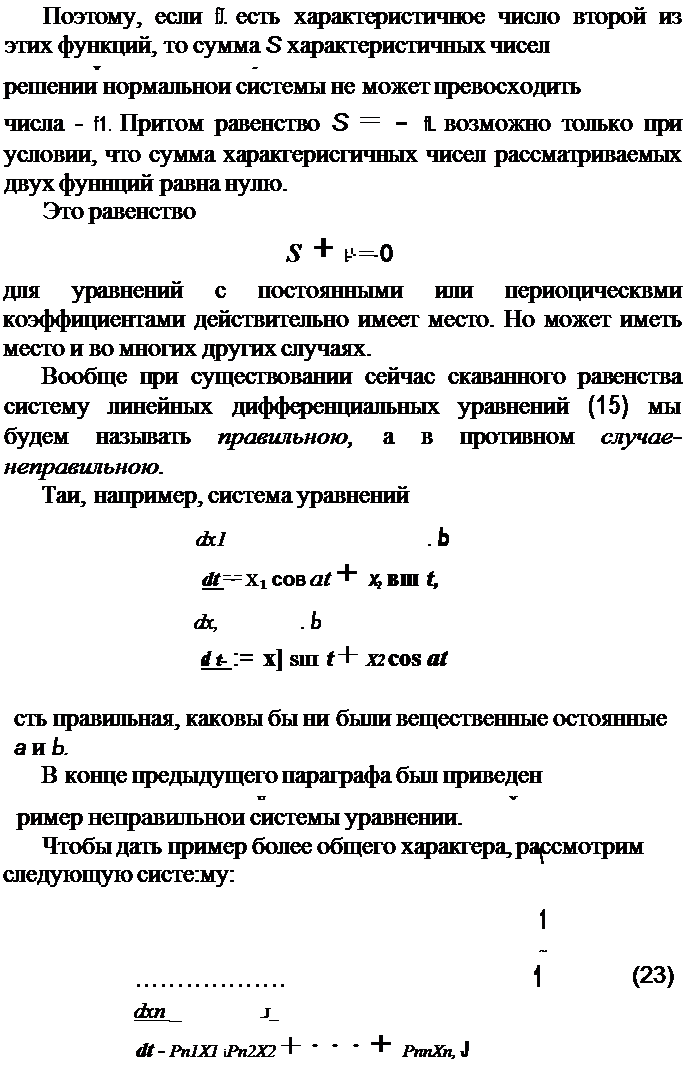~ dx которои уравнение, содержащее производную d/ , уннций х s', для которых s' > s.

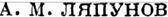
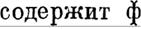
ОБЩАЯ ЗАДАЧА ОБ УСТОИЧИВОСТИ ДВИЖЕНИЯ

Относительно систем уравнений такого вида (в предположении, что коаффициенты Ps~ удовлетворяют прежним условиям) докажется следующее предложение. Т е о рем а. Для того, чтобы система ураенений (23) была правильною, необходимо и достаточно, чтобы симма хар ахтеристичных чисея функций

была равною нулю для всякого s. Докажем сначала необходимость этого условия. Для уравнений (23) находим следующую систему п V независимых решении : s-1 1) X1=eSv11dt, Xs=eSPs,dt ~ ~ PsiXte-Svssdtdt i -=-1

(s=2,3, ...,п), 2) х₁= О, х₂-=== eSP²²d\

(s=З,4, ... ,п),·

• • • • • • • • • • • • • • • • • • • • • • • • • t • • • •

Чтобы остановиться на чем-либо определенном, будем предполагать, что здесь все интегралы -~ Piidt, встречающиеся в показагелнх, обращаются в нуль при t = t₀• Что же касается остальных интегралов, то предположим их такими, чтобы в каком-либо k-ом решении фуннц:ии

-s-&

А.м.ляп~нов

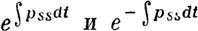
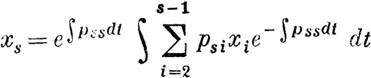
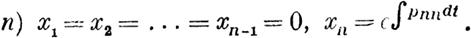
обращались при t = t₀в некоторые данные постоянные,

Тогда, если

есть k-oe решение рассматриваемой системы в предположении, 'Что все (Х равны нилю , то для того же k-го реше- u ния, не делая этого предположения, наидем: Xs = Xsk + a,k1 Xsk+ 1 + a,k2Xsk+ 2 + • · · + a,kn-kXsn (s=1,2, ... ,n). Отсюда на основании теоремы I предыдущего параграфа заключаем, что при надлежащем выборе постоянных а рассматриваемая система решений будет нормальною. Предполагая эти постоянные таким образом выбранными,означим характеристичные числа рассматриваемых решений соответственно через

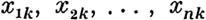
функции .eS Ps~dt

e-S Ps~dt

	fl-1, l-12, • • • , fLn•
Кроме того,	означим
		функции .eS Ps~dt				'
харантеристичное	число	функции .eS Ps~dt		через J"s,
			e-S Ps~dt			' '
	»	»	e-S Ps~dt		))	Лs,
			(s = 1, 2, ... , п),
))	))	))	ef ~ Pssdtчepeз S,
))	))	))	e-f~ Pssdt		»	S'.

Очевидно, будем иметь: ( s = 1, 2, ... , п). Поэтому, если допустим, что система (23) есть правильная, что приведет к равенству

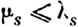
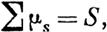
ОБЩАЯ ЗАДАЧА ОБ УСТОИЧИВОСТИ ДБИЖЕНИ

и ·заметим, что в силу леммы V сумма ~ J,₈не може быть более S, то найдем: ~ '\s=S. Но вследствие того же допущения имеем S + S' =0. Поэтому на основании леммы VII заключаем, чт характеристичное число функции ef ~Ps~dt е - f pkkdt равно S + лk, и что, следовательно (лемма V): s+ »; > ~ Лs-lЧо

V откуда вследствие только что наиденного равенства выводим: лk+ лi >О. Но сумма лk + ),i не может быть положительною; а потому

• Л1

ов

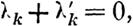
системе решений кажцый интеграл такого вида буде обладать характеристичным числом, не меньшим ха рактерисгичного числа подинтегральной функци (лемма VIII). Поэтому, если допустим, что ), s + ) ; == О ( s = 1, 2 , . . . , п) , и рассмотрим: какое-либо k-oe решение (в котором х₁, х₂, ••• , xk ₁равны нулю), то, замечал, что в этом решении харантерисгичным числом функции xk служит л1.:, легко убедимся, что характерисгичные числа всех остальных входящих в него функций не менее , .. ". Отсюда следует, что лk. есть характеристичное число k-го решения. Но мы имеем вообще ~ лs-< S-< - S' ~ - ~ ,.~, а вследствие допущенного ~ -. + ~ /1.s:::: О. Поэтому получаем равенство ~ ),s + S' = О, 113 которого выводим, 1) что система уравнений (23) есгь правильная и 2) что найденная для нее система решений есть нормальная. Примечание. На основании леммы VI выраженное в теореме условие равносильно следующему: каждая из функций

(s== 1, 2, ... , п)

(а если бы коэффициенты Pss были номплексными велиинами, то вещественная часть каждой из этих функ- 1ций) с беспредельным вовр астанием t должна приближаться К, некото рому пределу.

⇐ Предыдущая 1 2 345 6 7 8 Следующая ⇒