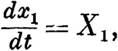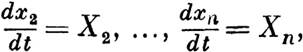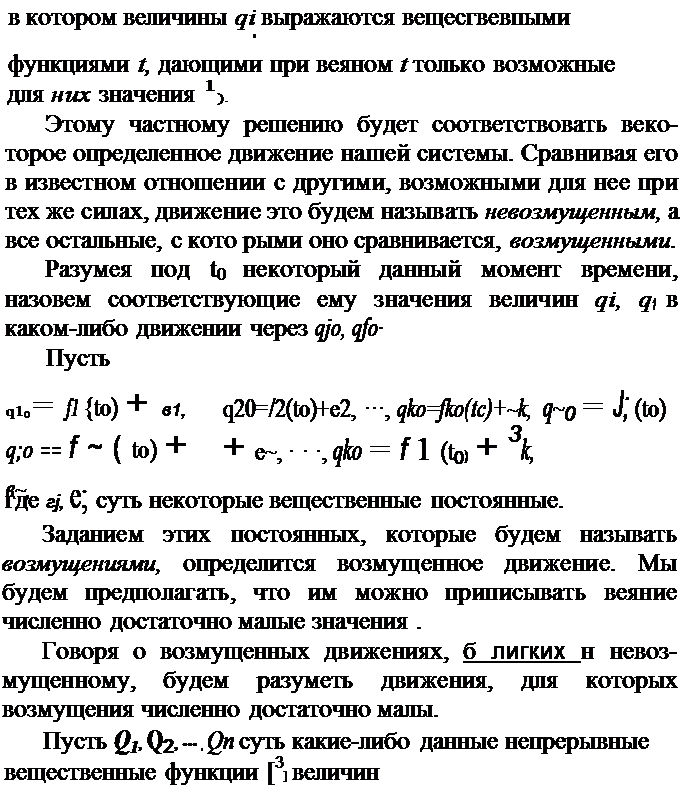Рнь>: У. 1 страница

Стр 1 из 8Следующая ⇒

JI А С С И К И ЕСТЕСТВОЗНАНИЯ

МАТЕМАТИКА МЕХАНИКА Ф ИЗ И К ААСТРОНОМИЯ

ГОСУд'А.РСТВЕН'tlОЕ ИЗДАТЁЛЬСТВОТЕХНИКО-ТЕОРЕТИЧЕСКОЙ литввсгтвы ' ~осква·19sо -сЛенинград

А.М. ЛЯПУНОlВ

ОБЩАЯ ЗАДАЧА ОБ УСТОЙЧИВОСТИ ДВИЖЕНИЯ

-Q)-

ГОСУДАРСТВЕННОЕИЗДАТЕЛЬСТВО ткхпик.о-твонвтич вскойЛИТЕРАТУРЫ гм ос к в а+в so -гленилсгоад

В этой книге помещены знаменитая докгорская диссертация гениального русского ученого Александра ихайловича Ляпунова «Общая задача об устойчи ости движсния», впервые опубликованная в издании Х арьновского математического общества в 1892 г., 11 три статьи А. М. Ляпунова, в иавестной мере допол яющие диссертацию. Диссертация и статьи написань япуновым больше, чем пятьдесят лет тому назад. Однако только в последние двадцать лет выявилась та огромная роль, ноторую имеют исследования Ляпунова ._, ля современнои технини . Тенет диссертации А. М.Ляпунова воспроизводите и са изменении; внесены лишь те исправления, которы были уназаны самим А. М.Ляпуновым в статье <<Н во росу об устойчивости движения». Нроме того, названия араграфов, данные А. М. Ляпуновым только в оглавлении, вставлены также в тенет книги. Аналогичным образом без изменения воспроизводится и тенет статей. В конце книги помещены небольшие примечания теисту А. М. Ляпунова, сделанные членом-норреспонентом Академии наук СССР Н. Г. Четаевым. Ссылки а эти примечания даны в теисте н квадратных скобках.

" Б УСТОИЧИВОСТ ДВИЖЕНИЯ

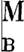
овив В этом сочинении излагаются некоторые способы V для решения вопросов о тех своиствах движения и в частности равновесия, которые известны под назва V V нием устоичивости и неустоичивости. Обыкновенные вопросы такого рода, которым и посвящено это сочинение, приводят н исследованию дифференциальных уравнений вида

вторые части которых, аависнщие от времен.и t и неизвестных его функций х₁, х₂, ••• , хп, при величинах Х₈, численно достаточно малых, разлагаются в ряды по целым положительным степеням последних и уничтожаются, когда все эти величины делаются нулями. Задача состоит при этом в том, чтобы узнать, можно ли начальные вначения функций Х₈, не делая их кулями,выбирать настолько численно малыми, чтобы во все время, следующее за начальным моментом, функции эти оставались численно меньшими некоторых заранее данных, отличных от нуля, но сколь угоди алых пределов. Ногда наши дифференциальные уравнения мы умее нтегрировать, задача эта конечно не представляе затруднений. Но важно иметь способы, которые повво л~ли бы решать ее независимо от выполнимости этого интегрирования.

А. М. ЛЯПУНОВ

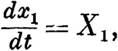
Известно, что существуют случаи, когда рассматриваемая задача допускает приведение н некогорой задаче о максимумах и минимумах ¹). Но область вопросов, которые таким путем могут быть разрешаемы, весьма ограничена, и в большинстве случаев необходимо прибегать R каким-либо иным методам. Прием, которым пользуются обыкновенно, приводится R тому, что в исследуемых дифференциальных уравнениях отбрасывают все члены выше первого измерения относительно величин xs и вместо первоначальных рассматривают получаемые таким путем линейные уравнения. Таи трактуется вопрос в сочинении Томсона и Тэта «Тгеапве оп Natural Philosophy>> (т. 1,ч. 1, 1879), в сочинениях Рауса <<А treatise оп the Stabllity of а gi ven State of шоыоп» ( 1877) и <<А treatise on the Dynamics of а System of rigid bodies» (ч. 11,4 изд., 1884) и нанонец-в сочинении Жуновсного <<0 прочности движенин» ( «Ученые записки Московского увиверситета»: отдел фиаико-математичвский, вып. 4, 1882) [¹]. Нонечно, указанный сейчас прием вносит весьма существенное упрощение, в особенности в тех случаях, когда коэффициенты в дифференциальных уравнениях суть постоянные величины. Но ааконность такого упрощения а priori ничем не оправдывается, ибо дело приво- u дится к замене рассматриваемои задачи другою, с кото- рою она может не находиться ни в канай зависимости. Во веяном случае очевидно, что если решение новой задачи и может давать ответ на первоначальную, то

¹) Мы разумеем здесь те случаи, н которым приложима известная теорема Лагранжа о максимумах и минимумах силовой функции, касающаяся вопросов об устойчивости равновесия, или более общая теорема Рауса о максимумах и минимумах известных интегралов дифференциальных уравнений движения, позволяющая решать некоторые вопросы об устойчивости движения (см. R о u t h, The advanced part of а treatise оп the Dynamics of а Syяtem of rigid bodies, 4 изд., стр. 52, 53).

ОБЩАЯ ЗАДАЧА ОБ УСТОЙЧИВОСТИ ДВИЖЕНИЯ 11

только при известных условиях, а последние обыкновенно не указываются. Дслжно, впрочем, заметить, что, сознавал нестрогость приема, некоторые авторы (иак, например, Раус) не ограничиваются одним первым приближением, н наторому приводит интегрирование названных выше линейных уравнений, а рассматривают также второе и некоторые из следующих, получаемых обычными в подобных случаях методами. Но этим дело мало подвигается вперед, ибо вообще таким путем достигается только более точное представление функций х₈в пределах известного промежутка времени, что, навечно, не дает новых оснований для каких-либо ааключений об устойчивости. Единственная, сколько мне известно, попытка строгого решения вопроса принадлежит А. Пуанкаре, который в своем во многих отношениях замечательном мемуаре «Зш les courbes definies par les equations differentielles>> (J ournal de mathematiques; 3 серия, томы 7 и 8; 4 серия, томы1 и 2) (¹], и именно в двух последних его частях, рассматривает вопросы об устойчивости для случая систем дифференциальных уравне- •.. нии второго порядка, а также останавливается на неко- т~рых блиаких н ним вопросах, касающихся систем третьего по рядка. Хотя Пуанкаре и ограничивается очень частными случаями, но методы, которыми он пользуется, допускают значительно более общие приложения и способны привести еще но многим новым результатам. Идеями, аанлючающимися в названном мемуаре, я руководствовался при большей части моих ивысканий. Задача, которую я себе поставил, предпринимая настоящее исследование, может быть формулирована таи: укааать те случаи, в которых первое приближение действительно решает вопрос об устойчивости, и дать накис-либо способы, которые позволяли бы решать его по крайней мере в некоторых из тех случаев, когда по первому приближению нельзя судить об устойчивости .

А, М, ЛЯПУНОВ

Конечно, чтобы придти н каким-либо результатам, необходимо было сделать относительно рассматриваемых дифференциальных уравнений известные предположения. Простейшее из них и вместе с тем соответствующее наиболее важным и интересным приложениям состояло бы в том, что коаффициенты в рааложениях V V вторых частеи этих уравнении суть постоянные ве- личины. Весьма многим интересным вопросам соответствовало бы также более общее предположение, что коаффициенты эти суть периодические функцви времени. В этих двух предположениях вопрос и трактуется мною преимущественно. Впрочем, я касаюсь отчасти и более общего случая, когда названные коэффициенты суть какие-либо фуикции времени, числовые значения которых никогда не превосходят иввестных пределов. В этом общем предположении трактуется вопрос в первой главе моего сочинения, где докааываегся одно предложение, касающееся интегрирования рассмаrг риваемых дифференциальных уравнений при помощи рядов известного типа ¹), и указываются некоторые выте- каюшие из него ааключения об устойчивости. В том же предположении цоказываютсн здесь и некоторые другие предложения, лежащие в основании дальнейших выводов. Первая глава представляет голъко вступительную часть моего сочинения, в которой излагаются некогорые предложения принципиального характера. Главную же часть составляют вторая и третья, где и рас-

¹) Ряды, о которых идет здесь речь, рассматривались мною в более частных првдположеппях в статье <<0 постоянных винтовых движениях твердого тела в жидкости» ( «Сообщ. Харьк. матем. общ.», 2 серия, том 1,1888). Впоследствии яузнал, что в таких же предположениях ряды эти рассматривались Пуанкаре в его диссертации «Вцг les propriete8 des fonctions uefinies par les equations aux differences рагйейев»( 1879).

ОБЩАЯ ЗАДАЧА ОБ УСТОЙЧИВОСТИ ДВИЖЕНИЯ

матриваются последовательно случаи постоянных и периодических коэффициентов. Иаждую из этих двух глав я начинаю некоторыми амочаниями, насающимися линейных дифференциальых уравнений, соответствующих первому приближвию, причем в третьей главе, где грактуотся случай ериодических коаффициентов, вхожу в неноторые одробности относительно так называемого ха рактери тичного уравнения. Переходя затем н главному вопросу и укавав условия, при которых он разрешается в первом приближении, я обращаюсь н тем особенным случаям, когда пля этой цели в цифференциальных уравнениях необходимо принимать в расчет члены выше первого измерения. Но случаи этого рода весьма разнообразны, и в на, ждом из них задача получает свой особый характер, таи что не может быть и речи о каких-либо общих способах ее решения, которые относились бы но всем таким случаям. Поэтому различные возможные случаи приходится рассматривать отдельно, и я ограничиваюсь только u простевшими ~3 них, которые представляют аатруц- пения, наименее серьезные. Исследование их и изложенив соответствующих им способов решения вопросов об устойчивости занимает большую часть двух последних глав. Не входя в дальнейшие подробности относительно содержания этого сочинения, с которым читатель может •.. до известпои степени ознакомитъся из прилагаемого u оглавления, замечу еще, что во второи главе я касаюсь вопроса о периодических решениях нелинейных дифференциальных уравнений. Вопрос этот находится u в теснои связи с методами, прилагаемыми мною для одного из особенных случаев. Притом рассмотрение его приводит R некоторым ааключениям об условной устой чивости для тех наиболее интересных случаев, когда дифференциальные уравнения имеют навоническу форму. А этими аанпючониями исчерпывается почт все, что пона можно снаэать общего о таних случаях.

А. М. ЛЯПУНОВ В предлагаемом сочинении читатель не найдет peme ния каних-либо определенных мех анических задач. По первоначальному плану приложения такого рода должны были составить четвертую главу. Но пото я отказался от намерения прибавлять ее, имея в виду следующие соображения. Все наиболее интересные и важные вопросы механики (как, например, те, когорые приводят н каноничесним уравнениям) таковы, что в особенных случаях, когда первое приближение недостаточно, задача делается для них в высшей степени трудною, и пока невозможно указать наких-либо приемов для ее решения. Поэтому, при рассмотрении таких вопросов, мне пришлось бы ограничиться только примерами двоякого рода: или теми, в которых вопрос решался бы приведением к задаче о максимумах и минимумах (т. е. на основании теоремы Рауса), или теми, в которых он решался бы в первом приближении. Но подобные примеры, хотя и представляли бы известный интерес, не относились бы u н главнои части моего исследования, которая, как уже было скааано, посвящена изложению методов, соответствующих особенным случаям известных категорий. Что же касается примеров, относящихся к этим методам, то их пришлось бы выбирать из области тех вопросов механики, в которых принимаются в расчет раз- ичного рода сопротивления среды. Таких примеров, онечно, можно было бы привести сколько угодно, но они сами по себе не представляли бы большого интереса и могли бы иметь значение только как поясняющие названные методы. Если же иметь в виду исключительно эту последнюю цель, то совершенно шостаточно и тех примеров аналитического характера, оторые приведены мною в надлежащих местах двух оследних глав. В ааключение замечу, что сочинение мое не есть ракгат об устойчивости, где было бы обязательно расмотрение механических задач веяного рода. Подобный рактат должен был бы заключать в себе многие вопросы, которых я здесь вовсе не касаюсь.

В этом сочинении я имел лишь в виду изложить то, то пока удалось мне сделать для решения поставлен ной мною задачи и что, может быть, может послужить u u точною отправления для дальнеиших иаыскапии акого же характера.

Во время печатания этого сочинения появились дв весьма интересных произведения А. Пуанкаре, в кото рых затрагиваются вопросы, стоящие весьма близко н рассматриваемым мною. Я разумею его мемуар «Зц le proЬleme des trois corps et les equations de la dyna-, шшце», появившийся в XIII томе Acta mathematica вскоре после того, как я начал печатать свое исслецо u u вание, и вышедшии в самое недавнее время первыи ом его большого сочинения <<Les methodes nouvelles de la Месапцше celeste>> (Paris, Gauthier-Villars, 1892). В первом находятся некоторые результаты, сходны с полученными мною, на что я и укавываю в падле ащих местах своего сочинения в подстрочных приме аниях. Что же касается второго, то овнаномитъся с ним подробно я еще не успел; но по отношению н во просам, рассматриваемым мною, в нем, повиди:мому, нет аких-либо существенных прибавлений н названному мемуару.

Считаю нужным скавать здесь об одном термине, встречающемся в этом сочинении. Рассматривая ряды, расположенные по степеням: величин, которые по ха рактеру вопроса можно предполагать сколь угодно малыми, я весьма часто говор о членах различных порядков. При этом под порядков каждого члена я разумею его измерение, и термин «порядок» не приписываю никаного иного значения. Я должен упомянуть еще об одном выражении, которым по примеру многих француаских и немецких ученых нередно пользуюсь для сон ращения речи.

А.М.ЛНПУНОВ

разумею выражение: «ряды, форма.лъпо удовлетворню ие» таким-то уравнениям. Выражение это имеет весьма условный смысл. Но я счел излишним входить в какие-либо разънснеия его, таи как в тех случаях, где мне приходится м пользоваться, относительно значения его не может V воэникнугь пикаких сомнении.

Это сочинение издано Харьковским математическим обществом, благодаря особым средствам, которые нашел возможным доставить ему Харьновский университет, за что и считаю долгом выразить последнему свою признательность.

Харьков, 5 аппеля 1892 г.

А. Ляпунов.

~--~- -Q 1 •

ГЛАВА I ш-вдвхгитвльныи АНА ЛИ3 ПОСТАНОВRА ВОПРОСА 1. Общая постановка задачи. Определение устойчивости.Рассмотрим накую-либо материальную систему с k степенями свободы. Пусть

суть k независимых переменных, которыми мы условились определять ее положение. Мыбудем предполагать, что за переменные эти взяты такие величины, которые остаются веществен- v u ными для всяких деиствительных положении системы. Рассматривая названные переменные как функции времени t, первые производные их по t будем обозначать через

Во веяной динамической задаче, в которой силы определенным образом заданы, эти функции будут удовлетворять некоторым k дифференциальным уравнениям второго порядна. Пусть для уравнений этих найдено какое-либо частное решение q1=f1(t), q2===f2(t), ... , qk==fk(t), 2 А. М. Ляпунов

А.М.ЛЯПУНОВ

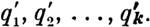
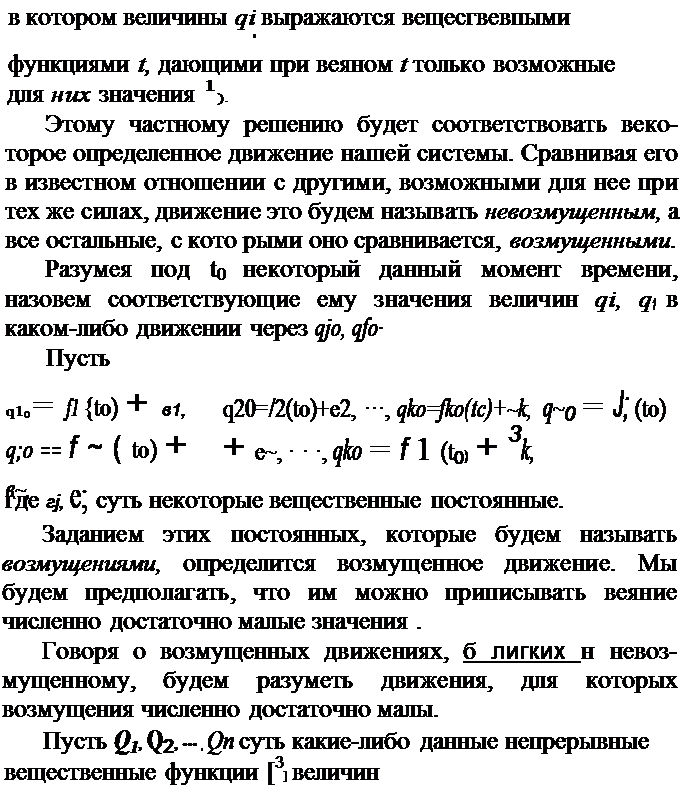Для невозмущенного движения они обратятся в некогорые известные функции t, которые означим соответственно через F1, F2, .•. , F n· Для возмущенного движения они будут некоторыми функциями величин

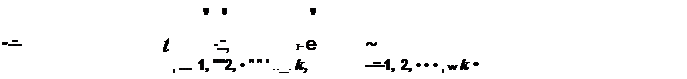¹) Мохсег случиться, что для величин q i по самому их выбору гоаможны не всякие вещественные значения, а только не большие или не меньшие известных П:Qеделов.

O:ВЩАН ЗАДАЧА ОБ УСТОЙЧИВОСТЙ движвния

Когда все в1, в₁равны нулю, величины Q1-F1, Q2-F2, ... ,Qn-Fn удут равными нулю для всякого t. Но если постояв ые ei, е;, не будучи нулями, предполагаются вс есконечно малыми, то является вопрос, можно ли азначитъ такие беснонечно малые пределы для велиин Qs-Fs, которых последние никогда не превзо шли бы по числовым значениям? Решение этого вопроса, который составит предмет наших иаыскапий, зависит как от характера рассмариваемого невозмущенного движения, таи и от выбора lфуннций Q₁, Q₂, ••• , Qn и момента времени t₀• При определенном выборе последних, ответ на этот вопрос удет, следовательно, характеризоватъ в известном отноении невозмущенное движение, определяя собою то свойство последнего, которое будем называть устойивостью, или противоположное ему, которое будем азыватъ неистойчивостью, Мы будем исключительно ааниматъся теми случаями, гогда решение_ рассматриваемого вопроса не зависит от выбора момента t₀, в который сообщаются возмуония. Поэтому примем здесь следующее опредеенив: Пусть L1, L2, ... , Е; суть проигваяьно задаваемые ояожительные числа. Если при всяких l.1₈, как бы они. алы ни были, могут бытъ выбириемы пояожитгльные числа Е1, Е2, ... , Ek, Е;, в;, ... , Ek так, чтобы при сяких вещественных е₁, s₁, удовлетворяющих условиям (j=1,2, ... ,k), при всяком t, превосходящем t₀, выпоянялись нер аенства

¹) Вообще под I х I условимся разуметь числовое значение вещественного или модуль мнимого количества х. *

12 3 4 5 6 7 8 Следующая ⇒