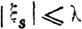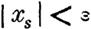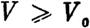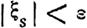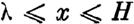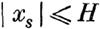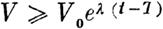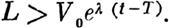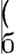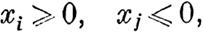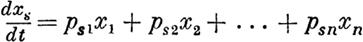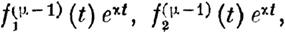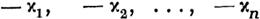Рнь>: У. 7 страница
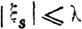
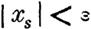

| | | | | | | | ОБЩАЯ РАДА ЧА ОБ УСТОйЧИВОСТИ~ДВИЖЕНИН
| | | | | | | | |  |
| | | | С этою целью рассмотрим какое-либо возмущенное движение, которому соответствуют величины ~s, числевно достаточно малые для того, чтобы условия (41) выполнялись во все время, следующее за моментом, когда t == Т.
.Пегко убедиться, что если постоянная Н достаточна мала, то при названных свойствах функции V (которую опять предположим определенно-положиельною) нельзя найти такого положительного числа l, оторое было бы меньше всех значений, получаемых функцией V в этом движении при t > Т.
В самом деле, если бы такое число существовало, то по свойствуV кан функции переменных (39), допуекающей бесконечно малый высший предел, мы нашли бы такое положительное число А., при котором было бы х > )\ ( если х попрежнему означает наибольшую из величин I », j) для всех значений t, превосходящих Т. А тогда для фуннции-V' при тех же значениях t существовал бы некоторый положительный низший предел l'.
Действительно, функцин - V', согласно допущенному, есть определенно-положительная. Поэтому постоянные Т и Н всегда можно предположить такими, чтобы при t >- Т и х < Н выполнялось условие-V' >- W', в котором W' есть некоторая независящая от положительная функция переменных х5, не уничтожающаяся при условии х < Н иначе, нан для х = О. Но этот последний случай будет исключен, если переменные xs подчинить условию
л < х < Н.
Поэтому при последнем функция W' будет иметь некоторый положительный низший предел l'.
Но если при t > Т всегда выполняется условие - V' > l', то иа уравнения (43) выведем
V<V0-l'(t-T)
для всех превосходящих Т значений t. А это невоз можно, ибо первая часть неравенства есть положитель-1
| | 
| | | | | | | | |  | 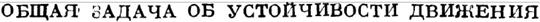
| | | | | | | | | | | | | | | | | | | |  | | | | | | | | | | | | | для всех значений t, превосходящих Т и удовлетво ряющих требованию, чтобы в промежутке от Т до условия (48) оставались постоянно выполненными.
Мы замечаем теперь, что по свойству фуннцви V
остоянную Т можно предположить достаточно большою для того, чтобы надлежащим выбором величин ~s, удовлетворяющих условиям
( s = 1, 2, ... , п),
| | | | | при веяном отличном от нуля, но сколь угодно малом положительном s, постоянную V0 можно было сделать
u
оложительнои.
Если же V0-положительная величина, то по свойству V как функции, цопускающвй бесконечно малый ысший предел, найдем такое положительное число л, которое будет менее всех значений, возможных при словии (51) (когда в нем предполагается t > Т) для наибольшей х из величин ! xs 1 • А тогда, если овнаим через l какое-либо положительное число, меньшее всех значений, возможных для функции W при условии
| |

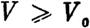
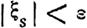
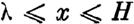


| | | | | | | | | ОБЩАЯ 3АДАЧА ОБ УСТОИЧИВОС'Тll движвния
| | | | | | | | |  |
| | | | | | | | | | | | | | | | | | | | | | | | | | Т е о р ем а III. Если дифференциальные уравиения возмущенного движения таковы, что возможно найти ограниченную функцию V, производная которой в силу этих уравнений приводилась бы к виду:
| | | | | | | | | | | | | | | где } ... =положитеяьная постоянная, а W или тождественно равна нулю, или представляет некоторрю внакопостояннцю функцию, и если в последнем случае найденная функция V такова, что при всяком t, большем некоторого предела, надлежащим выбором величин Х8, насколько угодно 'Численно малых, ее можно сделать величиною одинакового знака с W, - то невоемцшенное движение неистойчиво,
Пусть найденная функция V, удовлетворяющая этим требованиям, такова, что W есть фупкцин положительная.
По свойству функций V и W найдутся такие постоянные Т и Н, при которых для всех значений переменных, удовлетворя1ощих условиям: t :> Т и
| | | | | | (s==1,2, ... ,п), будут выполняться следующие:
1 V 1 < L, W > О,
| | | | | | | | | | где L-неноторая положительная постоянная. Притом постоянную Т можем предположить достаточно большою для того, чтобы надлежащим выбором значений ~s функций xs для t == Т, насколько угодно численно малых, соответствующее значение V0 функцив V можно было сделать положительным.
Рассматривая только не меньшие Т значения t, из уравнения (53) выведем:
dV -лV>О
| |
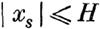
| | | | | | | | | | | | | | | | для всех значений t, при которых условии (54) остаются выполненными.
Поэтому если от Т до t условия эти постоянно выполняются, будем иметь:
| | | | | | | | Но при положительном V0 последнее неравенств может иметь место только для значений t, меньших величины
| | | |  | | | | Примечание. До сих пор мы предполагали, что для еременных х8 возможны веяние вещественные велиины, численно достаточно малые. Но могут встретиться случаи, когда, по самому значению этих переенных , для некоторых из них возможны величины олько одного из двух знаков (более сложных условий рассматриватъ не будем).
| |
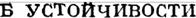

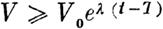
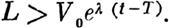

| | | | | | | | | | | | Для этого, конечно, дифференциальные уравнения 1) должны быть таковы, чтобы условия эти, которые удут вида
(55)
| | | | | выполнялись во все время движения, будучи выпол
u
ены в начальныи момент.
В этом случае в теоремах 11 и 111,при выражении ребования относительно звана функции V, условия (55) всегда должны быть подразумеваемы. Притом во всех предыдущих теоремах терминам «внанопостоян-
ая» или << знакоопределенная функция» доста точн приписывать более условное значение, которое он получили бы, если бы в определениях предыдущег араграфа предполагалось, что переменные подчи ноны не только условиям (40), но и условиям (55) [9].
| |
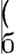
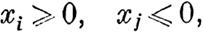
| | | | | | | --------------~c::::a--~-co:,i---------------
| | | | | ГЛАВА 11 исслвдовшив УСТАНОВИВШИХСЯ движвнии
О ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
17. Определяющее уравнение. Типы решений, соответствующие простым и кратным корням его. Группы решений.Рассмотрим систему линейных дифференциальных уравнений
(s=1,2, ... ,п) (1)
| | | | | | с постоянными коаффициентами Psa·
Интегрирование этой системы ваппг пт от rешrнт: п алгебраичесного уравнения
| |
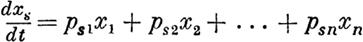
Р21 Р22 --х Р2п | Рн-х
| Р]2
| . . .
| Р1п
|
|
|
| | Р21
| Р22 --х
| • • •
| Р2п
|
|
|
|
|
|
|
| ==0
| |
|
|
|
|
|
|
|
| | . .
| . . . . . . . .
| . . .
| •
|
|
| | Рп1
| Рп2
| • • •
|
Рнь>: У.
|
|
| | | | | | | | | | | V V
п-ои степени относительно неиавестнои х.
Мы будем называть это уравнение определяющим, а определитель, представлнющий первую его частъ,--основным. Рассматривая последний как функппк величины х, будем означать его через D (х).
| |
| | | | | | | | | | | | | | | | | | | | | На,ндому корню х определяющего уравнения соответствует решение системы ( 1) вида
X1=-=K1ext, X2=K2ext, ... ' Xn=Knext, (2)
| | | | |  | | | | 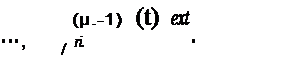 | | | | Мы будем говорить, что в этом случае корню х соот-
v
ветствует одна группа решении.
Случай этот представится веяний раз, когда рассматриваемый корень х не обращает в нуль по крайней 1мере одного из первых миноров основного определителя.
| |
| | | | | ОБЩАЯ ЗАДАЧАОБ УСТОЙЧИВОСТИ ДВИЖЕНИЯ 97
Может случиться, что р-нратвый корень х обращает в нуль все миноры этого определителя до порядна k -1 включительно, не обращая в нуль по крайней мере одного из миноров k-го порядна.
Тогда корню этому будет соответствовать k групп независимых решений, составленных подобно предыдущей.
Высшим пределом для числа k служит число fJ,.
Этот высший предел может достигаться, и тогда все решения, соответствующие корню х, будут типа (2).
Все эти теоремы можно считать настолько хорошо всем известными, что было бы излишним приводить их доказательства, которые притом не представляют
U V
ни малеиших 3а труднении.
Заметим, что если х1, х2, ••• , xn суть все корни определяющего уравнения, то вещественные части величин
| | | | | представят для уравнений (1) то, что мы назвали характеристичными числами системы линейных дифферен-
u
циальных уравнении.
18. Линейное преобразование дифференциальных уравнений н некоторому простейшему виду.Для системы уравнений (1) можно найти п независимых интегралов вида
У1Х1 + У2Х2 + · · · + УпХп, где Ys суть некоторые функции t.
Функции эти будут удовлетворять системе уравнений
| | | | | dy8
dt + PisYL + P2sY2 + · · · + PnsYn = О (s --= 1, 2, • .. , n), (3)
| |
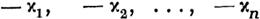
| присоединенной к ( 1), и если
|
|
| |
|